Declaración del problema:
dado un gráfico que representa una red de flujo donde cada borde tiene una capacidad. También dados dos vértices fuente ‘s’ y sumidero ‘t’ en el gráfico, encuentre el flujo máximo posible de s a t con las siguientes restricciones:
- El flujo en un borde no excede la capacidad dada del borde.
- Un flujo entrante es igual a un flujo saliente para cada vértice excepto s y t.
Por ejemplo:
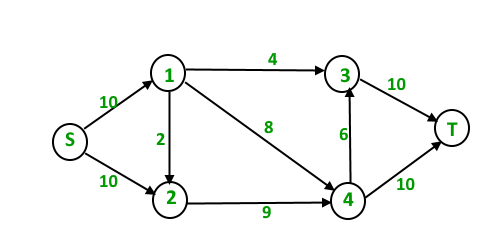
En el siguiente gráfico de entrada,
el flujo máximo de st es 19, que se muestra a continuación.

Fondo :
- Introducción al problema de flujo máximo : presentamos el problema de flujo máximo, discutimos el algoritmo codicioso e introdujimos el gráfico residual.
- Algoritmo de Ford-Fulkerson e implementación de Edmond Karp : discutimos el algoritmo de Ford-Fulkerson y su implementación. También discutimos el gráfico residual en detalle.
La complejidad temporal de la implementación de Edmond Karp es O(VE 2 ). En esta publicación, se analiza un nuevo algoritmo de Dinic que es un algoritmo más rápido y toma O (EV 2 ).
Al igual que el algoritmo de Edmond Karp, el algoritmo de Dinic utiliza los siguientes conceptos:
- Un flujo es máximo si no hay un camino de s a t en el gráfico residual.
- BFS se utiliza en un bucle. Sin embargo, hay una diferencia en la forma en que usamos BFS en ambos algoritmos.
En el algoritmo Karp de Edmond , usamos BFS para encontrar una ruta de aumento y enviar el flujo a través de esta ruta. En el algoritmo de Dinic, usamos BFS para verificar si es posible un mayor flujo y para construir un gráfico de nivel. En el gráfico de nivel , asignamos niveles a todos los Nodes, el nivel de un Node es la distancia más corta (en términos de número de bordes) del Node desde la fuente. Una vez que se construye el gráfico de nivel, enviamos múltiples flujos utilizando este gráfico de nivel. Esta es la razón por la que funciona mejor que Edmond Karp. En Edmond Karp, enviamos solo el flujo que se envía a través de la ruta encontrada por BFS.
Esquema del algoritmo de Dinic:
- Inicialice el gráfico residual G como gráfico dado.
- Realice BFS de G para construir un gráfico de nivel (o asigne niveles a los vértices) y también compruebe si es posible un mayor flujo.
- Si no es posible más flujo, entonces regrese
- Envíe múltiples flujos en G usando el gráfico de nivel hasta que se alcance el flujo de bloqueo .
Aquí , el uso de gráficos de nivel significa que, en cada flujo, los niveles de los Nodes de ruta deben ser 0, 1, 2… (en orden) de s a t.
Un flujo es flujo de bloqueo si no se puede enviar más flujo usando el gráfico de nivel, es decir, no existe más ruta st de modo que los vértices de la ruta tengan los niveles actuales 0, 1, 2… en orden. El flujo de bloqueo se puede ver igual que la ruta de flujo máximo en el algoritmo Greedy discutido aquí .
Ilustración:
Gráfico residual inicial (igual que el gráfico dado)
Flujo total = 0
Primera iteración: asignamos niveles a todos los Nodes usando BFS. También verificamos si es posible más flujo (o si hay un camino st en el gráfico residual).

Ahora encontramos el flujo de bloqueo usando niveles (significa que cada ruta de flujo debe tener niveles como 0, 1, 2, 3). Enviamos tres flujos juntos. Aquí es donde está optimizado en comparación con Edmond Karp, donde enviamos un flujo a la vez.
4 unidades de flujo en el camino s – 1 – 3 – t.
6 unidades de flujo en el camino s – 1 – 4 – t.
4 unidades de flujo en el camino s – 2 – 4 – t.
Flujo total = Flujo total + 4 + 6 + 4 = 14
Después de una iteración, el gráfico residual cambia al siguiente.

Segunda iteración: asignamos nuevos niveles a todos los Nodes usando BFS del gráfico residual modificado anterior. También verificamos si es posible más flujo (o si hay un camino st en el gráfico residual).

Ahora encontramos el flujo de bloqueo usando niveles (significa que cada ruta de flujo debe tener niveles como 0, 1, 2, 3, 4). Solo podemos enviar un flujo esta vez.
5 unidades de caudal en la trayectoria s – 2 – 4 – 3 – t
Caudal total = Caudal total + 5 = 19
El nuevo gráfico residual es

Tercera iteración: ejecutamos BFS y creamos un gráfico de nivel. También verificamos si es posible más flujo y procedemos solo si es posible. Esta vez no hay ruta st en el gráfico residual, por lo que terminamos el algoritmo.
Implementación:
a continuación se muestra la implementación en C++ del algoritmo de Dinic:
CPP
// C++ implementation of Dinic's Algorithm
#include <bits/stdc++.h>
using namespace std;
// A structure to represent a edge between
// two vertex
struct Edge {
int v; // Vertex v (or "to" vertex)
// of a directed edge u-v. "From"
// vertex u can be obtained using
// index in adjacent array.
int flow; // flow of data in edge
int C; // capacity
int rev; // To store index of reverse
// edge in adjacency list so that
// we can quickly find it.
};
// Residual Graph
class Graph {
int V; // number of vertex
int* level; // stores level of a node
vector<Edge>* adj;
public:
Graph(int V)
{
adj = new vector<Edge>[V];
this->V = V;
level = new int[V];
}
// add edge to the graph
void addEdge(int u, int v, int C)
{
// Forward edge : 0 flow and C capacity
Edge a{ v, 0, C, (int)adj[v].size() };
// Back edge : 0 flow and 0 capacity
Edge b{ u, 0, 0, (int)adj[u].size() };
adj[u].push_back(a);
adj[v].push_back(b); // reverse edge
}
bool BFS(int s, int t);
int sendFlow(int s, int flow, int t, int ptr[]);
int DinicMaxflow(int s, int t);
};
// Finds if more flow can be sent from s to t.
// Also assigns levels to nodes.
bool Graph::BFS(int s, int t)
{
for (int i = 0; i < V; i++)
level[i] = -1;
level[s] = 0; // Level of source vertex
// Create a queue, enqueue source vertex
// and mark source vertex as visited here
// level[] array works as visited array also.
list<int> q;
q.push_back(s);
vector<Edge>::iterator i;
while (!q.empty()) {
int u = q.front();
q.pop_front();
for (i = adj[u].begin(); i != adj[u].end(); i++) {
Edge& e = *i;
if (level[e.v] < 0 && e.flow < e.C) {
// Level of current vertex is,
// level of parent + 1
level[e.v] = level[u] + 1;
q.push_back(e.v);
}
}
}
// IF we can not reach to the sink we
// return false else true
return level[t] < 0 ? false : true;
}
// A DFS based function to send flow after BFS has
// figured out that there is a possible flow and
// constructed levels. This function called multiple
// times for a single call of BFS.
// flow : Current flow send by parent function call
// start[] : To keep track of next edge to be explored.
// start[i] stores count of edges explored
// from i.
// u : Current vertex
// t : Sink
int Graph::sendFlow(int u, int flow, int t, int start[])
{
// Sink reached
if (u == t)
return flow;
// Traverse all adjacent edges one -by - one.
for (; start[u] < adj[u].size(); start[u]++) {
// Pick next edge from adjacency list of u
Edge& e = adj[u][start[u]];
if (level[e.v] == level[u] + 1 && e.flow < e.C) {
// find minimum flow from u to t
int curr_flow = min(flow, e.C - e.flow);
int temp_flow
= sendFlow(e.v, curr_flow, t, start);
// flow is greater than zero
if (temp_flow > 0) {
// add flow to current edge
e.flow += temp_flow;
// subtract flow from reverse edge
// of current edge
adj[e.v][e.rev].flow -= temp_flow;
return temp_flow;
}
}
}
return 0;
}
// Returns maximum flow in graph
int Graph::DinicMaxflow(int s, int t)
{
// Corner case
if (s == t)
return -1;
int total = 0; // Initialize result
// Augment the flow while there is path
// from source to sink
while (BFS(s, t) == true) {
// store how many edges are visited
// from V { 0 to V }
int* start = new int[V + 1]{ 0 };
// while flow is not zero in graph from S to D
while (int flow = sendFlow(s, INT_MAX, t, start))
// Add path flow to overall flow
total += flow;
}
// return maximum flow
return total;
}
// Driver Code
int main()
{
Graph g(6);
g.addEdge(0, 1, 16);
g.addEdge(0, 2, 13);
g.addEdge(1, 2, 10);
g.addEdge(1, 3, 12);
g.addEdge(2, 1, 4);
g.addEdge(2, 4, 14);
g.addEdge(3, 2, 9);
g.addEdge(3, 5, 20);
g.addEdge(4, 3, 7);
g.addEdge(4, 5, 4);
// next exmp
/*g.addEdge(0, 1, 3 );
g.addEdge(0, 2, 7 ) ;
g.addEdge(1, 3, 9);
g.addEdge(1, 4, 9 );
g.addEdge(2, 1, 9 );
g.addEdge(2, 4, 9);
g.addEdge(2, 5, 4);
g.addEdge(3, 5, 3);
g.addEdge(4, 5, 7 );
g.addEdge(0, 4, 10);
// next exp
g.addEdge(0, 1, 10);
g.addEdge(0, 2, 10);
g.addEdge(1, 3, 4 );
g.addEdge(1, 4, 8 );
g.addEdge(1, 2, 2 );
g.addEdge(2, 4, 9 );
g.addEdge(3, 5, 10 );
g.addEdge(4, 3, 6 );
g.addEdge(4, 5, 10 ); */
cout << "Maximum flow " << g.DinicMaxflow(0, 5);
return 0;
}
Python3
# Python implementation of Dinic's Algorithm
class Edge:
def __init__(self, v, flow, C, rev):
self.v = v
self.flow = flow
self.C = C
self.rev = rev
# Residual Graph
class Graph:
def __init__(self, V):
self.adj = [[] for i in range(V)]
self.V = V
self.level = [0 for i in range(V)]
# add edge to the graph
def addEdge(self, u, v, C):
# Forward edge : 0 flow and C capacity
a = Edge(v, 0, C, len(self.adj[v]))
# Back edge : 0 flow and 0 capacity
b = Edge(u, 0, 0, len(self.adj[u]))
self.adj[u].append(a)
self.adj[v].append(b)
# Finds if more flow can be sent from s to t
# Also assigns levels to nodes
def BFS(self, s, t):
for i in range(self.V):
self.level[i] = -1
# Level of source vertex
self.level[s] = 0
# Create a queue, enqueue source vertex
# and mark source vertex as visited here
# level[] array works as visited array also
q = []
q.append(s)
while q:
u = q.pop(0)
for i in range(len(self.adj[u])):
e = self.adj[u][i]
if self.level[e.v] < 0 and e.flow < e.C:
# Level of current vertex is
# level of parent + 1
self.level[e.v] = self.level[u]+1
q.append(e.v)
# If we can not reach to the sink we
# return False else True
return False if self.level[t] < 0 else True
# A DFS based function to send flow after BFS has
# figured out that there is a possible flow and
# constructed levels. This functions called multiple
# times for a single call of BFS.
# flow : Current flow send by parent function call
# start[] : To keep track of next edge to be explored
# start[i] stores count of edges explored
# from i
# u : Current vertex
# t : Sink
def sendFlow(self, u, flow, t, start):
# Sink reached
if u == t:
return flow
# Traverse all adjacent edges one -by -one
while start[u] < len(self.adj[u]):
# Pick next edge from adjacency list of u
e = self.adj[u][start[u]]
if self.level[e.v] == self.level[u]+1 and e.flow < e.C:
# find minimum flow from u to t
curr_flow = min(flow, e.C-e.flow)
temp_flow = self.sendFlow(e.v, curr_flow, t, start)
# flow is greater than zero
if temp_flow and temp_flow > 0:
# add flow to current edge
e.flow += temp_flow
# subtract flow from reverse edge
# of current edge
self.adj[e.v][e.rev].flow -= temp_flow
return temp_flow
start[u] += 1
# Returns maximum flow in graph
def DinicMaxflow(self, s, t):
# Corner case
if s == t:
return -1
# Initialize result
total = 0
# Augument the flow while there is path
# from source to sink
while self.BFS(s, t) == True:
# store how many edges are visited
# from V { 0 to V }
start = [0 for i in range(self.V+1)]
while True:
flow = self.sendFlow(s, float('inf'), t, start)
if not flow:
break
# Add path flow to overall flow
total += flow
# return maximum flow
return total
g = Graph(6)
g.addEdge(0, 1, 16)
g.addEdge(0, 2, 13)
g.addEdge(1, 2, 10)
g.addEdge(1, 3, 12)
g.addEdge(2, 1, 4)
g.addEdge(2, 4, 14)
g.addEdge(3, 2, 9)
g.addEdge(3, 5, 20)
g.addEdge(4, 3, 7)
g.addEdge(4, 5, 4)
print("Maximum flow", g.DinicMaxflow(0, 5))
# This code is contributed by rupasriachanta421.
Maximum flow 23
Tiempo Complejidad : O (EV 2 ) .
- Hacer un BFS para construir un gráfico de nivel lleva tiempo O (E).
- El envío de varios flujos más hasta que se alcanza un flujo de bloqueo lleva tiempo O(VE).
- El bucle externo se ejecuta como máximo en el tiempo O(V).
- En cada iteración, construimos un nuevo gráfico de nivel y encontramos un flujo de bloqueo. Se puede probar que la cantidad de niveles aumenta al menos en uno en cada iteración (consulte el video de referencia a continuación para ver la prueba). Entonces, el ciclo externo se ejecuta en la mayoría de los tiempos O (V).
- Por lo tanto, la complejidad global del tiempo es O(EV 2 ).
Este artículo es una contribución de Nishant Singh . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA