Un árbol de búsqueda binario (BST) es una estructura de datos de árbol binario basada en Nodes que tiene las siguientes propiedades.
- El subárbol izquierdo de un Node contiene solo Nodes con claves menores que la clave del Node.
- El subárbol derecho de un Node contiene solo Nodes con claves mayores que la clave del Node.
- Los subárboles izquierdo y derecho también deben ser árboles de búsqueda binarios.
De las propiedades anteriores se deduce naturalmente que:
- Cada Node (elemento en el árbol) tiene una clave distinta.
MÉTODO 1 (Simple pero incorrecto) El
siguiente es un programa simple. Para cada Node, compruebe si el Node izquierdo es menor que el Node y si el Node derecho es mayor que el Node.
C++
int isBST(struct node* node)
{
if (node == NULL)
return 1;
/* false if left is > than node */
if (node->left != NULL && node->left->data > node->data)
return 0;
/* false if right is < than node */
if (node->right != NULL && node->right->data < node->data)
return 0;
/* false if, recursively, the left or right is not a BST */
if (!isBST(node->left) || !isBST(node->right))
return 0;
/* passing all that, it's a BST */
return 1;
}
// This code is contributed by shubhamsingh10
C
int isBST(struct node* node)
{
if (node == NULL)
return 1;
/* false if left is > than node */
if (node->left != NULL && node->left->data > node->data)
return 0;
/* false if right is < than node */
if (node->right != NULL && node->right->data < node->data)
return 0;
/* false if, recursively, the left or right is not a BST */
if (!isBST(node->left) || !isBST(node->right))
return 0;
/* passing all that, it's a BST */
return 1;
}
Java
boolean isBST(Node node)
{
if (node == null)
return true;
/* False if left is > than node */
if (node.left != null && node.left.data > node.data)
return false;
/* False if right is < than node */
if (node.right != null && node.right.data < node.data)
return false;
/* False if, recursively, the left or right is not a BST */
if (!isBST(node.left) || !isBST(node.right))
return false;
/* Passing all that, it's a BST */
return true;
}
// This code is contributed by shubhamsingh10
Python3
def isBST(node): if (node == None): return 1 ''' false if left is > than node ''' if (node.left != None and node.left.data > node.data): return 0 ''' false if right is < than node ''' if (node.right != None and node.right.data < node.data): return 0 ''' false if, recursively, the left or right is not a BST ''' if (!isBST(node.left) or !isBST(node.right)): return 0 ''' passing all that, it's a BST ''' return 1 # This code is contributed by Shubham Singh
C#
bool isBST(Node node)
{
if (node == null)
return true;
/* False if left is > than node */
if (node.left != null && node.left.data > node.data)
return false;
/* False if right is < than node */
if (node.right != null && node.right.data < node.data)
return false;
/* False if, recursively, the left or right is not a BST */
if (!isBST(node.left) || !isBST(node.right))
return false;
/* Passing all that, it's a BST */
return true;
}
// This code is contributed by Rajput-Ji
Javascript
<script>
function isBST(node)
{
if (node == null)
return true;
/* False if left is > than node */
if (node.left != null && node.left.data > node.data)
return false;
/* False if right is < than node */
if (node.right != null && node.right.data < node.data)
return false;
/* False if, recursively, the left or right is not a BST */
if (!isBST(node.left) || !isBST(node.right))
return false;
/* Passing all that, it's a BST */
return true;
}
// This code is contributed by avanitrachhadiya2155
</script>
Complejidad de tiempo: O(n)
Mientras visitamos cada Node solo una vez
Espacio Auxiliar: O(h)
Aquí h es la altura del árbol y el espacio adicional se usa debido a la pila de llamadas de función.
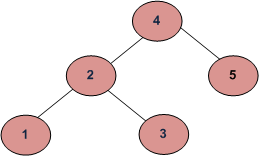
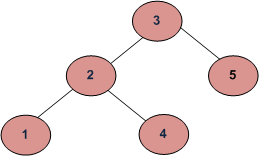
Este enfoque es incorrecto ya que devolverá verdadero para el árbol binario inferior (y el árbol inferior no es un BST porque 4 está en el subárbol izquierdo de 3)
MÉTODO 2 (Correcto pero no eficiente)
Para cada Node, verifique si el valor máximo en el subárbol izquierdo es más pequeño que el Node y el valor mínimo en el subárbol derecho es mayor que el Node.
C++
/* Returns true if a binary tree is a binary search tree */
int isBST(struct node* node)
{
if (node == NULL)
return 1;
/* false if the max of the left is > than us */
if (node->left != NULL && maxValue(node->left) >= node->data)
return 0;
/* false if the min of the right is <= than us */
if (node->right != NULL && minValue(node->right) <= node->data)
return 0;
/* false if, recursively, the left or right is not a BST */
if (!isBST(node->left) || !isBST(node->right))
return 0;
/* passing all that, it's a BST */
return 1;
}
// This code is contributed by shubhamsingh10
C
/* Returns true if a binary tree is a binary search tree */
int isBST(struct node* node)
{
if (node == NULL)
return 1;
/* false if the max of the left is > than us */
if (node->left!=NULL && maxValue(node->left) > node->data)
return 0;
/* false if the min of the right is <= than us */
if (node->right!=NULL && minValue(node->right) < node->data)
return 0;
/* false if, recursively, the left or right is not a BST */
if (!isBST(node->left) || !isBST(node->right))
return 0;
/* passing all that, it's a BST */
return 1;
}
Java
/* Returns true if a binary tree is a binary search tree */
int isBST(Node node)
{
if (node == null)
return 1;
/* false if the max of the left is > than us */
if (node.left != null && maxValue(node.left) >= node.data)
return 0;
/* false if the min of the right is <= than us */
if (node.right != null && minValue(node.right) <= node.data)
return 0;
/* false if, recursively, the left or right is not a BST */
if (!isBST(node.left) || !isBST(node.right))
return 0;
/* passing all that, it's a BST */
return 1;
}
// This code is contributed by akshitsaxenaa09.
Python3
''' Returns true if a binary tree is a binary search tree ''' def isBST(node): if (node == None): return 1 ''' false if the max of the left is > than us ''' if (node.left != None and maxValue(node.left) >= node.data): return 0 ''' false if the min of the right is <= than us ''' if (node.right != None and minValue(node.right) <= node.data): return 0 ''' false if, recursively, the left or right is not a BST ''' if (!isBST(node.left) or !isBST(node.right)): return 0 ''' passing all that, it's a BST ''' return 1 # This code is contributed by Shubham Singh
C#
/* Returns true if a binary tree is a binary search tree */
bool isBST(Node node)
{
if (node == null)
return true;
/* false if the max of the left is > than us */
if (node.left != null && maxValue(node.left) >= node.data)
return false;
/* false if the min of the right is <= than us */
if (node.right != null && minValue(node.right) <= node.data)
return false;
/* false if, recursively, the left or right is not a BST */
if (!isBST(node.left) || !isBST(node.right))
return false;
/* passing all that, it's a BST */
return true;
}
// This code is contributed by Shubham Singh
Javascript
<script>
function isBST(node)
{
if (node == null)
return true;
/* False if the max of the left is > than us */
if (node.left != null && maxValue(node.left) >= node.data)
return false;
/* False if the min of the right is <= than us */
if (node.right != null && minValue(node.right) <= node.data)
return false;
/* False if, recursively, the left or right is not a BST */
if (!isBST(node.left) || !isBST(node.right))
return false;
/* Passing all that, it's a BST */
return true;
}
// This code is contributed by Shubham Singh
</script>
Se supone que tiene funciones auxiliares minValue() y maxValue() que devuelven el valor int mínimo o máximo de un árbol no vacío
Complejidad del tiempo: O(n^2)
Como visitamos cada Node solo una vez y nuestro método auxiliar también toma el tiempo O(n), entonces la complejidad del tiempo general se convierte en O(n) * O(n) = O(n^2)
Espacio Auxiliar: O(h)
Aquí h es la altura del árbol y el espacio adicional se usa debido a la pila de llamadas de función.
MÉTODO 3 (Correcto y Eficiente) : El
Método 2 anterior funciona lentamente ya que atraviesa algunas partes del árbol muchas veces. Una mejor solución mira cada Node solo una vez. El truco consiste en escribir una función auxiliar de utilidad isBSTUtil(struct node* node, int min, int max) que recorre el árbol manteniendo un registro de los valores mínimos y máximos permitidos a medida que avanza, observando cada Node solo una vez. Los valores iniciales para min y max deben ser INT_MIN e INT_MAX; se reducen a partir de ahí.
Nota: Este método no es aplicable si hay elementos duplicados con valor INT_MIN o INT_MAX.
A continuación se muestra la implementación del enfoque anterior:
C++
#include<bits/stdc++.h>
using namespace std;
/* A binary tree node has data,
pointer to left child and
a pointer to right child */
class node
{
public:
int data;
node* left;
node* right;
/* Constructor that allocates
a new node with the given data
and NULL left and right pointers. */
node(int data)
{
this->data = data;
this->left = NULL;
this->right = NULL;
}
};
int isBSTUtil(node* node, int min, int max);
/* Returns true if the given
tree is a binary search tree
(efficient version). */
int isBST(node* node)
{
return(isBSTUtil(node, INT_MIN, INT_MAX));
}
/* Returns true if the given
tree is a BST and its values
are >= min and <= max. */
int isBSTUtil(node* node, int min, int max)
{
/* an empty tree is BST */
if (node==NULL)
return 1;
/* false if this node violates
the min/max constraint */
if (node->data < min || node->data > max)
return 0;
/* otherwise check the subtrees recursively,
tightening the min or max constraint */
return
isBSTUtil(node->left, min, node->data-1) && // Allow only distinct values
isBSTUtil(node->right, node->data+1, max); // Allow only distinct values
}
/* Driver code*/
int main()
{
node *root = new node(4);
root->left = new node(2);
root->right = new node(5);
root->left->left = new node(1);
root->left->right = new node(3);
if(isBST(root))
cout<<"Is BST";
else
cout<<"Not a BST";
return 0;
}
// This code is contributed by rathbhupendra
C
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>
/* A binary tree node has data, pointer to left child
and a pointer to right child */
struct node
{
int data;
struct node* left;
struct node* right;
};
int isBSTUtil(struct node* node, int min, int max);
/* Returns true if the given tree is a binary search tree
(efficient version). */
int isBST(struct node* node)
{
return(isBSTUtil(node, INT_MIN, INT_MAX));
}
/* Returns true if the given tree is a BST and its
values are >= min and <= max. */
int isBSTUtil(struct node* node, int min, int max)
{
/* an empty tree is BST */
if (node==NULL)
return 1;
/* false if this node violates the min/max constraint */
if (node->data < min || node->data > max)
return 0;
/* otherwise check the subtrees recursively,
tightening the min or max constraint */
return
isBSTUtil(node->left, min, node->data-1) && // Allow only distinct values
isBSTUtil(node->right, node->data+1, max); // Allow only distinct values
}
/* Helper function that allocates a new node with the
given data and NULL left and right pointers. */
struct node* newNode(int data)
{
struct node* node = (struct node*)
malloc(sizeof(struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return(node);
}
/* Driver program to test above functions*/
int main()
{
struct node *root = newNode(4);
root->left = newNode(2);
root->right = newNode(5);
root->left->left = newNode(1);
root->left->right = newNode(3);
if(isBST(root))
printf("Is BST");
else
printf("Not a BST");
getchar();
return 0;
}
Java
//Java implementation to check if given Binary tree
//is a BST or not
/* Class containing left and right child of current
node and key value*/
class Node
{
int data;
Node left, right;
public Node(int item)
{
data = item;
left = right = null;
}
}
public class BinaryTree
{
//Root of the Binary Tree
Node root;
/* can give min and max value according to your code or
can write a function to find min and max value of tree. */
/* returns true if given search tree is binary
search tree (efficient version) */
boolean isBST() {
return isBSTUtil(root, Integer.MIN_VALUE,
Integer.MAX_VALUE);
}
/* Returns true if the given tree is a BST and its
values are >= min and <= max. */
boolean isBSTUtil(Node node, int min, int max)
{
/* an empty tree is BST */
if (node == null)
return true;
/* false if this node violates the min/max constraints */
if (node.data < min || node.data > max)
return false;
/* otherwise check the subtrees recursively
tightening the min/max constraints */
// Allow only distinct values
return (isBSTUtil(node.left, min, node.data-1) &&
isBSTUtil(node.right, node.data+1, max));
}
/* Driver program to test above functions */
public static void main(String args[])
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(4);
tree.root.left = new Node(2);
tree.root.right = new Node(5);
tree.root.left.left = new Node(1);
tree.root.left.right = new Node(3);
if (tree.isBST())
System.out.println("IS BST");
else
System.out.println("Not a BST");
}
}
Python3
# Python program to check if a binary tree is bst or not
INT_MAX = 4294967296
INT_MIN = -4294967296
# A binary tree node
class Node:
# Constructor to create a new node
def __init__(self, data):
self.data = data
self.left = None
self.right = None
# Returns true if the given tree is a binary search tree
# (efficient version)
def isBST(node):
return (isBSTUtil(node, INT_MIN, INT_MAX))
# Retusn true if the given tree is a BST and its values
# >= min and <= max
def isBSTUtil(node, mini, maxi):
# An empty tree is BST
if node is None:
return True
# False if this node violates min/max constraint
if node.data < mini or node.data > maxi:
return False
# Otherwise check the subtrees recursively
# tightening the min or max constraint
return (isBSTUtil(node.left, mini, node.data -1) and
isBSTUtil(node.right, node.data+1, maxi))
# Driver program to test above function
root = Node(4)
root.left = Node(2)
root.right = Node(5)
root.left.left = Node(1)
root.left.right = Node(3)
if (isBST(root)):
print ("Is BST")
else:
print ("Not a BST")
# This code is contributed by Nikhil Kumar Singh(nickzuck_007)
C#
using System;
// C# implementation to check if given Binary tree
//is a BST or not
/* Class containing left and right child of current
node and key value*/
public class Node
{
public int data;
public Node left, right;
public Node(int item)
{
data = item;
left = right = null;
}
}
public class BinaryTree
{
//Root of the Binary Tree
public Node root;
/* can give min and max value according to your code or
can write a function to find min and max value of tree. */
/* returns true if given search tree is binary
search tree (efficient version) */
public virtual bool BST
{
get
{
return isBSTUtil(root, int.MinValue, int.MaxValue);
}
}
/* Returns true if the given tree is a BST and its
values are >= min and <= max. */
public virtual bool isBSTUtil(Node node, int min, int max)
{
/* an empty tree is BST */
if (node == null)
{
return true;
}
/* false if this node violates the min/max constraints */
if (node.data < min || node.data > max)
{
return false;
}
/* otherwise check the subtrees recursively
tightening the min/max constraints */
// Allow only distinct values
return (isBSTUtil(node.left, min, node.data - 1) && isBSTUtil(node.right, node.data + 1, max));
}
/* Driver program to test above functions */
public static void Main(string[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(4);
tree.root.left = new Node(2);
tree.root.right = new Node(5);
tree.root.left.left = new Node(1);
tree.root.left.right = new Node(3);
if (tree.BST)
{
Console.WriteLine("IS BST");
}
else
{
Console.WriteLine("Not a BST");
}
}
}
// This code is contributed by Shrikant13
Javascript
<script>
// Javascript implementation to
// check if given Binary tree
// is a BST or not
/* Class containing left and right child of current
node and key value*/
class Node
{
constructor(item)
{
this.data=item;
this.left=this.right=null;
}
}
//Root of the Binary Tree
let root;
/* can give min and max value according to your code or
can write a function to find min and max value of tree. */
/* returns true if given search tree is binary
search tree (efficient version) */
function isBST()
{
return isBSTUtil(root, Number.MIN_VALUE,
Number.MAX_VALUE);
}
/* Returns true if the given tree is a BST and its
values are >= min and <= max. */
function isBSTUtil(node,min,max)
{
/* an empty tree is BST */
if (node == null)
return true;
/* false if this node violates
the min/max constraints */
if (node.data < min || node.data > max)
return false;
/* otherwise check the subtrees recursively
tightening the min/max constraints */
// Allow only distinct values
return (isBSTUtil(node.left, min, node.data-1) &&
isBSTUtil(node.right, node.data+1, max));
}
/* Driver program to test above functions */
root = new Node(4);
root.left = new Node(2);
root.right = new Node(5);
root.left.left = new Node(1);
root.left.right = new Node(3);
if (isBST())
document.write("IS BST<br>");
else
document.write("Not a BST<br>");
// This code is contributed by rag2127
</script>
Producción:
IS BST
Complejidad de tiempo: O(n)
Espacio auxiliar: O(1) si no se considera el tamaño de la pila de llamadas a funciones, de lo contrario, O(h) donde h es la altura del árbol
Método simplificado 3
Podemos simplificar el método 2 usando punteros NULL en lugar de INT_MIN y valores INT_MAX.
C++
// C++ program to check if a given tree is BST.
#include <bits/stdc++.h>
using namespace std;
/* A binary tree node has data, pointer to
left child and a pointer to right child */
struct Node
{
int data;
struct Node* left, *right;
};
// Returns true if given tree is BST.
bool isBST(Node* root, Node* l=NULL, Node* r=NULL)
{
// Base condition
if (root == NULL)
return true;
// if left node exist then check it has
// correct data or not i.e. left node's data
// should be less than root's data
if (l != NULL and root->data <= l->data)
return false;
// if right node exist then check it has
// correct data or not i.e. right node's data
// should be greater than root's data
if (r != NULL and root->data >= r->data)
return false;
// check recursively for every node.
return isBST(root->left, l, root) and
isBST(root->right, root, r);
}
/* Helper function that allocates a new node with the
given data and NULL left and right pointers. */
struct Node* newNode(int data)
{
struct Node* node = new Node;
node->data = data;
node->left = node->right = NULL;
return (node);
}
/* Driver program to test above functions*/
int main()
{
struct Node *root = newNode(3);
root->left = newNode(2);
root->right = newNode(5);
root->left->left = newNode(1);
root->left->right = newNode(4);
if (isBST(root,NULL,NULL))
cout << "Is BST";
else
cout << "Not a BST";
return 0;
}
Java
// Java program to check if a given tree is BST.
class Sol
{
// A binary tree node has data, pointer to
//left child && a pointer to right child /
static class Node
{
int data;
Node left, right;
};
// Returns true if given tree is BST.
static boolean isBST(Node root, Node l, Node r)
{
// Base condition
if (root == null)
return true;
// if left node exist then check it has
// correct data or not i.e. left node's data
// should be less than root's data
if (l != null && root.data <= l.data)
return false;
// if right node exist then check it has
// correct data or not i.e. right node's data
// should be greater than root's data
if (r != null && root.data >= r.data)
return false;
// check recursively for every node.
return isBST(root.left, l, root) &&
isBST(root.right, root, r);
}
// Helper function that allocates a new node with the
//given data && null left && right pointers. /
static Node newNode(int data)
{
Node node = new Node();
node.data = data;
node.left = node.right = null;
return (node);
}
// Driver code
public static void main(String args[])
{
Node root = newNode(3);
root.left = newNode(2);
root.right = newNode(5);
root.left.left = newNode(1);
root.left.right = newNode(4);
if (isBST(root,null,null))
System.out.print("Is BST");
else
System.out.print("Not a BST");
}
}
// This code is contributed by Arnab Kundu
Python3
""" Program to check if a given Binary
Tree is balanced like a Red-Black Tree """
# Helper function that allocates a new
# node with the given data and None
# left and right poers.
class newNode:
# Construct to create a new node
def __init__(self, key):
self.data = key
self.left = None
self.right = None
# Returns true if given tree is BST.
def isBST(root, l = None, r = None):
# Base condition
if (root == None) :
return True
# if left node exist then check it has
# correct data or not i.e. left node's data
# should be less than root's data
if (l != None and root.data <= l.data) :
return False
# if right node exist then check it has
# correct data or not i.e. right node's data
# should be greater than root's data
if (r != None and root.data >= r.data) :
return False
# check recursively for every node.
return isBST(root.left, l, root) and \
isBST(root.right, root, r)
# Driver Code
if __name__ == '__main__':
root = newNode(3)
root.left = newNode(2)
root.right = newNode(5)
root.right.left = newNode(1)
root.right.right = newNode(4)
#root.right.left.left = newNode(40)
if (isBST(root,None,None)):
print("Is BST")
else:
print("Not a BST")
# This code is contributed by
# Shubham Singh(SHUBHAMSINGH10)
C#
// C# program to check if a given tree is BST.
using System;
class GFG
{
// A binary tree node has data, pointer to
//left child && a pointer to right child /
public class Node
{
public int data;
public Node left, right;
};
// Returns true if given tree is BST.
static Boolean isBST(Node root, Node l, Node r)
{
// Base condition
if (root == null)
return true;
// if left node exist then check it has
// correct data or not i.e. left node's data
// should be less than root's data
if (l != null && root.data <= l.data)
return false;
// if right node exist then check it has
// correct data or not i.e. right node's data
// should be greater than root's data
if (r != null && root.data >= r.data)
return false;
// check recursively for every node.
return isBST(root.left, l, root) &&
isBST(root.right, root, r);
}
// Helper function that allocates a new node with the
//given data && null left && right pointers. /
static Node newNode(int data)
{
Node node = new Node();
node.data = data;
node.left = node.right = null;
return (node);
}
// Driver code
public static void Main(String []args)
{
Node root = newNode(3);
root.left = newNode(2);
root.right = newNode(5);
root.left.left = newNode(1);
root.left.right = newNode(4);
if (isBST(root,null,null))
Console.Write("Is BST");
else
Console.Write("Not a BST");
}
}
// This code is contributed by 29AjayKumar
Javascript
<script>
// JavaScript program to check if a given tree is BST.
class Node
{
constructor(data) {
this.left = null;
this.right = null;
this.data = data;
}
}
// Returns true if given tree is BST.
function isBST(root, l, r)
{
// Base condition
if (root == null)
return true;
// if left node exist then check it has
// correct data or not i.e. left node's data
// should be less than root's data
if (l != null && root.data <= l.data)
return false;
// if right node exist then check it has
// correct data or not i.e. right node's data
// should be greater than root's data
if (r != null && root.data >= r.data)
return false;
// check recursively for every node.
return isBST(root.left, l, root) &&
isBST(root.right, root, r);
}
// Helper function that allocates a new node with the
//given data && null left && right pointers. /
function newNode(data)
{
let node = new Node(data);
return (node);
}
let root = newNode(3);
root.left = newNode(2);
root.right = newNode(5);
root.left.left = newNode(1);
root.left.right = newNode(4);
if (isBST(root,null,null))
document.write("Is BST");
else
document.write("Not a BST");
</script>
Producción:
Not a BST
Complejidad de tiempo: O(n)
Mientras visitamos cada Node solo una vez
Espacio Auxiliar: O(h)
Aquí h es la altura del árbol y el espacio adicional se usa debido a la pila de llamadas de función.
Gracias a Abhinesh Garhwal por sugerir la solución anterior.
MÉTODO 4 (Uso de recorrido en orden)
Gracias a LJW489 por sugerir este método.
1) Realice un recorrido en orden del árbol dado y almacene el resultado en una array temporal.
2) Este método asume que no hay valores duplicados en el árbol
3) Verifique si la array temporal está ordenada en orden ascendente, si es así, entonces el árbol es BST.
Complejidad de Tiempo: O(n)
Podemos evitar el uso de un Auxiliary Array. Mientras realizamos el recorrido en orden, podemos realizar un seguimiento del Node visitado anteriormente. Si el valor del Node visitado actualmente es menor que el valor anterior, entonces el árbol no es BST. Gracias a ygos por esta optimización del espacio.
C++
bool isBST(node* root)
{
static node *prev = NULL;
// traverse the tree in inorder fashion
// and keep track of prev node
if (root)
{
if (!isBST(root->left))
return false;
// Allows only distinct valued nodes
if (prev != NULL &&
root->data <= prev->data)
return false;
prev = root;
return isBST(root->right);
}
return true;
}
// This code is contributed by rathbhupendra
C
bool isBST(struct node* root)
{
static struct node *prev = NULL;
// traverse the tree in inorder fashion and keep track of prev node
if (root)
{
if (!isBST(root->left))
return false;
// Allows only distinct valued nodes
if (prev != NULL && root->data <= prev->data)
return false;
prev = root;
return isBST(root->right);
}
return true;
}
Java
// Java implementation to check if given Binary tree
// is a BST or not
/* Class containing left and right child of current
node and key value*/
class Node
{
int data;
Node left, right;
public Node(int item)
{
data = item;
left = right = null;
}
}
public class BinaryTree
{
// Root of the Binary Tree
Node root;
// To keep tract of previous node in Inorder Traversal
Node prev;
boolean isBST() {
prev = null;
return isBST(root);
}
/* Returns true if given search tree is binary
search tree (efficient version) */
boolean isBST(Node node)
{
// traverse the tree in inorder fashion and
// keep a track of previous node
if (node != null)
{
if (!isBST(node.left))
return false;
// allows only distinct values node
if (prev != null && node.data <= prev.data )
return false;
prev = node;
return isBST(node.right);
}
return true;
}
/* Driver program to test above functions */
public static void main(String args[])
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(4);
tree.root.left = new Node(2);
tree.root.right = new Node(5);
tree.root.left.left = new Node(1);
tree.root.left.right = new Node(3);
if (tree.isBST())
System.out.println("IS BST");
else
System.out.println("Not a BST");
}
}
Python3
# Python implementation to check if
# given Binary tree is a BST or not
# A binary tree node containing data
# field, left and right pointers
class Node:
# constructor to create new node
def __init__(self, val):
self.data = val
self.left = None
self.right = None
# global variable prev - to keep track
# of previous node during Inorder
# traversal
prev = None
# function to check if given binary
# tree is BST
def isbst(root):
# prev is a global variable
global prev
prev = None
return isbst_rec(root)
# Helper function to test if binary
# tree is BST
# Traverse the tree in inorder fashion
# and keep track of previous node
# return true if tree is Binary
# search tree otherwise false
def isbst_rec(root):
# prev is a global variable
global prev
# if tree is empty return true
if root is None:
return True
if isbst_rec(root.left) is False:
return False
# if previous node'data is found
# greater than the current node's
# data return false
if prev is not None and prev.data > root.data:
return False
# store the current node in prev
prev = root
return isbst_rec(root.right)
# driver code to test above function
root = Node(4)
root.left = Node(2)
root.right = Node(5)
root.left.left = Node(1)
root.left.right = Node(3)
if isbst(root):
print("is BST")
else:
print("not a BST")
# This code is contributed by
# Shweta Singh(shweta44)
C#
// C# implementation to check if
// given Binary tree is a BST or not
using System;
/* Class containing left and
right child of current node
and key value*/
class Node
{
public int data;
public Node left, right;
public Node(int item)
{
data = item;
left = right = null;
}
}
public class BinaryTree
{
// Root of the Binary Tree
Node root;
// To keep tract of previous node
// in Inorder Traversal
Node prev;
Boolean isBST()
{
prev = null;
return isBST(root);
}
/* Returns true if given search tree is binary
search tree (efficient version) */
Boolean isBST(Node node)
{
// traverse the tree in inorder fashion and
// keep a track of previous node
if (node != null)
{
if (!isBST(node.left))
return false;
// allows only distinct values node
if (prev != null &&
node.data <= prev.data )
return false;
prev = node;
return isBST(node.right);
}
return true;
}
// Driver Code
public static void Main(String []args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(4);
tree.root.left = new Node(2);
tree.root.right = new Node(5);
tree.root.left.left = new Node(1);
tree.root.left.right = new Node(3);
if (tree.isBST())
Console.WriteLine("IS BST");
else
Console.WriteLine("Not a BST");
}
}
// This code is contributed by Rajput-Ji
Javascript
<script>
// Javascript implementation to check if given Binary tree
// is a BST or not
/* Class containing left and right child of current
node and key value*/
class Node
{
constructor(item)
{
this.data = item;
this.left = this.right=null;
}
}
// Root of the Binary Tree
let root;
// To keep tract of previous node in Inorder Traversal
let prev;
function isBST()
{
prev = null;
return _isBST(root);
}
/* Returns true if given search tree is binary
search tree (efficient version) */
function _isBST(node)
{
// traverse the tree in inorder fashion and
// keep a track of previous node
if (node != null)
{
if (!_isBST(node.left))
return false;
// allows only distinct values node
if (prev != null && node.data <= prev.data )
return false;
prev = node;
return _isBST(node.right);
}
return true;
}
/* Driver program to test above functions */
root = new Node(4);
root.left = new Node(2);
root.right = new Node(5);
root.left.left = new Node(1);
root.left.right = new Node(3);
if (isBST())
document.write("IS BST");
else
document.write("Not a BST");
// This code is contributed by unknown2108
</script>
El uso de una variable estática también se puede evitar utilizando una referencia al Node anterior como parámetro.
C++
// C++ program to check if a given tree is BST.
#include <bits/stdc++.h>
using namespace std;
/* A binary tree node has data, pointer to
left child and a pointer to right child */
struct Node
{
int data;
struct Node* left, *right;
Node(int data)
{
this->data = data;
left = right = NULL;
}
};
bool isBSTUtil(struct Node* root, Node *&prev)
{
// traverse the tree in inorder fashion and
// keep track of prev node
if (root)
{
if (!isBSTUtil(root->left, prev))
return false;
// Allows only distinct valued nodes
if (prev != NULL && root->data <= prev->data)
return false;
prev = root;
return isBSTUtil(root->right, prev);
}
return true;
}
bool isBST(Node *root)
{
Node *prev = NULL;
return isBSTUtil(root, prev);
}
/* Driver program to test above functions*/
int main()
{
struct Node *root = new Node(3);
root->left = new Node(2);
root->right = new Node(5);
root->left->left = new Node(1);
root->left->right = new Node(4);
if (isBST(root))
cout << "Is BST";
else
cout << "Not a BST";
return 0;
}
Java
// Java program to check if a given tree is BST.
import java.io.*;
class GFG {
/* A binary tree node has data, pointer to
left child and a pointer to right child */
public static class Node
{
public int data;
public Node left, right;
public Node(int data)
{
this.data = data;
left = right = null;
}
};
static Node prev;
static Boolean isBSTUtil(Node root)
{
// traverse the tree in inorder fashion and
// keep track of prev node
if (root != null)
{
if (!isBSTUtil(root.left))
return false;
// Allows only distinct valued nodes
if (prev != null &&
root.data <= prev.data)
return false;
prev = root;
return isBSTUtil(root.right);
}
return true;
}
static Boolean isBST(Node root)
{
return isBSTUtil(root);
}
// Driver Code
public static void main (String[] args)
{
Node root = new Node(3);
root.left = new Node(2);
root.right = new Node(5);
root.left.left = new Node(1);
root.left.right = new Node(4);
if (isBST(root))
System.out.println("Is BST");
else
System.out.println("Not a BST");
}
}
// This code is contributed by Shubham Singh
Python3
# Python3 program to check
# if a given tree is BST.
import math
# A binary tree node has data,
# pointer to left child and
# a pointer to right child
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
def isBSTUtil(root, prev):
# traverse the tree in inorder fashion
# and keep track of prev node
if (root != None):
if (isBSTUtil(root.left, prev) == True):
return False
# Allows only distinct valued nodes
if (prev != None and
root.data <= prev.data):
return False
prev = root
return isBSTUtil(root.right, prev)
return True
def isBST(root):
prev = None
return isBSTUtil(root, prev)
# Driver Code
if __name__ == '__main__':
root = Node(3)
root.left = Node(2)
root.right = Node(5)
root.right.left = Node(1)
root.right.right = Node(4)
#root.right.left.left = Node(40)
if (isBST(root) == None):
print("Is BST")
else:
print("Not a BST")
# This code is contributed by Srathore
C#
// C# program to check if a given tree is BST.
using System;
public class GFG
{
/* A binary tree node has data, pointer to
left child and a pointer to right child */
public class Node
{
public int data;
public Node left, right;
public Node(int data)
{
this.data = data;
left = right = null;
}
};
static Node prev;
static Boolean isBSTUtil(Node root)
{
// traverse the tree in inorder fashion and
// keep track of prev node
if (root != null)
{
if (!isBSTUtil(root.left))
return false;
// Allows only distinct valued nodes
if (prev != null &&
root.data <= prev.data)
return false;
prev = root;
return isBSTUtil(root.right);
}
return true;
}
static Boolean isBST(Node root)
{
return isBSTUtil(root);
}
// Driver Code
public static void Main(String[] args)
{
Node root = new Node(3);
root.left = new Node(2);
root.right = new Node(5);
root.left.left = new Node(1);
root.left.right = new Node(4);
if (isBST(root))
Console.WriteLine("Is BST");
else
Console.WriteLine("Not a BST");
}
}
// This code is contributed by Rajput-Ji
Javascript
<script>
// Javascript program to check if a given tree is BST.
class Node
{
constructor(data)
{
this.left = null;
this.right = null;
this.data = data;
}
}
let prev;
function isBSTUtil(root)
{
// traverse the tree in inorder fashion and
// keep track of prev node
if (root != null)
{
if (!isBSTUtil(root.left))
return false;
// Allows only distinct valued nodes
if (prev != null && root.data <= prev.data)
return false;
prev = root;
return isBSTUtil(root.right);
}
return true;
}
function isBST(root)
{
return isBSTUtil(root);
}
let root = new Node(3);
root.left = new Node(2);
root.right = new Node(5);
root.left.left = new Node(1);
root.left.right = new Node(4);
if (isBST(root))
document.write("Is BST");
else
document.write("Not a BST");
// This code is contributed by divyeshrabadiya07.
</script>
Salida :
Not a BST
Complejidad de tiempo: O(n)
Mientras visitamos cada Node solo una vez
Espacio Auxiliar: O(h)
Aquí h es la altura del árbol y el espacio adicional se usa debido a la pila de llamadas de función.
Fuentes:
http://en.wikipedia.org/wiki/Binary_search_tree
http://cslibrary.stanford.edu/110/BinaryTrees.html
Escriba comentarios si encuentra algún error en los programas/algoritmos anteriores u otras formas de resolver el el mismo problema.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA