Árbol Gomory-Hu | Serie 1 (Introducción)

Antecedentes:
en una red de flujo, un corte st es un corte que requiere que la fuente ‘s’ y el sumidero ‘t’ estén en diferentes subconjuntos, y consiste en bordes que van desde el lado de la fuente hasta el lado del sumidero. La capacidad de un corte de st se define por la suma de la capacidad de cada borde en el conjunto de cortes. (Fuente: Wiki ). Dados dos vértices, s y t, podemos encontrar el corte mínimo de st usando el algoritmo de flujo máximo .

Dado que hay un total de O(n ² ) pares posibles, a primera vista parece que habría un total de O(n ² ) valores mínimos totales de corte de st. Pero cuando usamos Gomory-Hu Tree, vemos que hay un total de n-1 valores de corte diferentes [Un árbol con n vértices tiene n-1 bordes]

Problemas gráficos populares que se pueden resolver usando Gomory-Hu Tree:

1. Dado un gráfico ponderado y conectado, encuentre el corte de punto mínimo para todos los pares de vértices. O un problema como encontrar el mínimo de todos los cortes de pt mínimos posibles.
2. Problema de corte K mínimo : encuentre el conjunto de aristas de peso mínimo cuya eliminación dividiría el gráfico en k componentes conectados. Este es un problema NP-Hard, Gomory-Hu Tree proporciona una solución aproximada para este problema.

¿Qué es el árbol Gomory-Hu ?
Se define un árbol de Gomory-Hu para un gráfico de flujo con función de capacidad de borde c. El árbol tiene el mismo conjunto de vértices que el gráfico de entrada y tiene n-1 (n es el número de vértices) bordes. La función de capacidad de borde c’ se define usando las siguientes propiedades:

Árbol de flujo equivalente: para cualquier par de vértices s y t, el corte mínimo de st en el gráfico es igual a la capacidad más pequeña de los bordes en el camino entre s y t en Tree.

Propiedad de corte: un corte de st mínimo en Tree también es un corte mínimo en Graph.G

Por ejemplo, considere el siguiente gráfico y el árbol de Gomory-Hu correspondiente.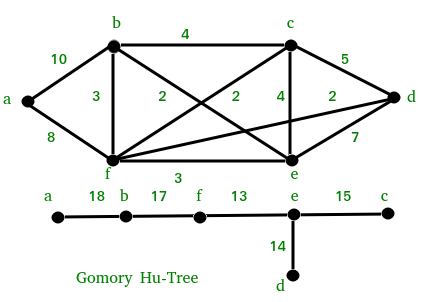

Dado que hay n-1 aristas en un árbol con n Nodes, podemos concluir que hay como máximo n-1 valores de flujo diferentes en una red de flujo con n vértices.

Discutiremos la construcción de Tree en la próxima publicación.

¿Cómo se construyen los problemas anteriores utilizando Gomory-Hu Tree?
El borde de peso mínimo en el árbol es el mínimo de todos los cortes de pt.

Podemos resolver el problema del corte k siguiendo los pasos a continuación.
1) Construya el Árbol Gomory-Hu.
2) Retire los bordes de peso mínimo k-1 (o los más livianos) del árbol.
3) Unión de retorno de los componentes obtenida por el desborde anterior.

El siguiente diagrama ilustra el algoritmo anterior.

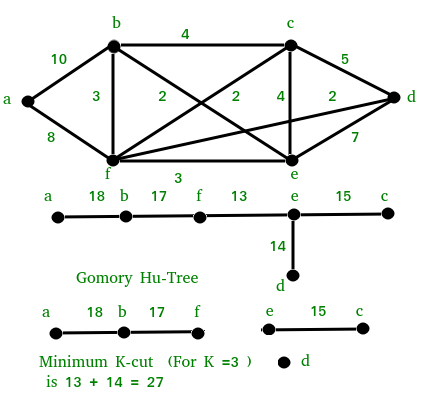
Tenga en cuenta que es posible que la solución anterior no siempre produzca un resultado óptimo, pero se garantiza que producirá resultados dentro de los límites de (2-2/k).

Referencias:
https://www.corelab.ntua.gr/seminar/material/2008-2009/2008.10.20.Gomory-Hu%20trees%20and%20applications.slides.pdf
https://courses.engr.illinois.edu /cs598csc/sp2009/lectures/lecture_7.pdf
https://cseweb.ucsd.edu/classes/fa06/cse202/Gomory-Hu%20Tree.pdf

Este artículo es una contribución de Dheeraj Gupta . Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.