La función Totient de Euler Φ(n) para una entrada n es el recuento de números en {1, 2, 3, …, n} que son primos relativos a n, es decir, los números cuyo MCD (máximo común divisor) con n es 1 .
Por ejemplo, Φ(4) = 2, Φ(3) = 2 y Φ(5) = 4. Hay 2 números menores o iguales a 4 que son primos relativos a 4, 2 números menores o iguales a 3 que son relativamente primos a 3. Y 4 números menores o iguales a 5 que son primos relativos a 5.
Hemos discutido diferentes métodos para el cálculo de Φ(n) en la publicación anterior .
¿Cómo calcular Φ para todos los números menores o iguales que n?
Ejemplo:
Input: n = 5
Output: Totient of 1 is 1
Totient of 2 is 1
Totient of 3 is 2
Totient of 4 is 2
Totient of 5 is 4
Le recomendamos encarecidamente que minimice su navegador y que pruebe esto usted mismo primero.
Una solución simple es llamar Φ(i) para i = 1 an.
Una solución eficiente es usar una idea similar a la criba de Eratóstenes para calcular previamente todos los valores. El método se basa en la siguiente fórmula del producto.

La fórmula básicamente dice que el valor de Φ(n) es igual a n multiplicado por el subproducto de (1 – 1/p) para todos los factores primos p de n. Por ejemplo, valor de Φ(6) = 6 * (1-1/2) * (1 – 1/3) = 2.
A continuación se muestra el algoritmo completo:
1) Create an array phi[1..n] to store Φ values of all numbers
from 1 to n.
2) Initialize all values such that phi[i] stores i. This
initialization serves two purposes.
a) To check if phi[i] is already evaluated or not. Note that
the maximum possible phi value of a number i is i-1.
b) To initialize phi[i] as i is multiple in the above product
formula.
3) Run a loop for p = 2 to n
a) If phi[p] is p, means p is not evaluated yet and p is a
prime number (similar to Sieve), otherwise phi[p] must
have been updated in step 3.b
b) Traverse through all multiples of p and update all
multiples of p by multiplying with (1-1/p).
4) Run a loop from i = 1 to n and print all Ph[i] values.
A continuación se muestra la implementación del algoritmo anterior.
C++
// C++ program to compute Totient function for
// all numbers smaller than or equal to n.
#include<iostream>
using namespace std;
// Computes and prints totient of all numbers
// smaller than or equal to n.
void computeTotient(int n)
{
// Create and initialize an array to store
// phi or totient values
long long phi[n+1];
for (int i=1; i<=n; i++)
phi[i] = i; // indicates not evaluated yet
// and initializes for product
// formula.
// Compute other Phi values
for (int p=2; p<=n; p++)
{
// If phi[p] is not computed already,
// then number p is prime
if (phi[p] == p)
{
// Phi of a prime number p is
// always equal to p-1.
phi[p] = p-1;
// Update phi values of all
// multiples of p
for (int i = 2*p; i<=n; i += p)
{
// Add contribution of p to its
// multiple i by multiplying with
// (1 - 1/p)
phi[i] = (phi[i]/p) * (p-1);
}
}
}
// Print precomputed phi values
for (int i=1; i<=n; i++)
cout << "Totient of " << i << " is "
<< phi[i] << endl;
}
// Driver program to test above function
int main()
{
int n = 12;
computeTotient(n);
return 0;
}
Java
// Java program to compute Totient
// function for all numbers smaller
// than or equal to n.
import java.util.*;
class GFG {
// Computes and prints totient of all numbers
// smaller than or equal to n.
static void computeTotient(int n) {
// Create and initialize an array to store
// phi or totient values
long phi[] = new long[n + 1];
for (int i = 1; i <= n; i++)
phi[i] = i; // indicates not evaluated yet
// and initializes for product
// formula.
// Compute other Phi values
for (int p = 2; p <= n; p++) {
// If phi[p] is not computed already,
// then number p is prime
if (phi[p] == p) {
// Phi of a prime number p is
// always equal to p-1.
phi[p] = p - 1;
// Update phi values of all
// multiples of p
for (int i = 2 * p; i <= n; i += p) {
// Add contribution of p to its
// multiple i by multiplying with
// (1 - 1/p)
phi[i] = (phi[i] / p) * (p - 1);
}
}
}
// Print precomputed phi values
for (int i = 1; i <= n; i++)
System.out.println("Totient of " + i +
" is " + phi[i]);
}
// Driver code
public static void main(String[] args) {
int n = 12;
computeTotient(n);
}
}
// This code is contributed by Anant Agarwal.
Python3
# Python program to compute
# Totient function for
# all numbers smaller than
# or equal to n.
# Computes and prints
# totient of all numbers
# smaller than or equal to n.
def computeTotient(n):
# Create and initialize
# an array to store
# phi or totient values
phi=[]
for i in range(n + 2):
phi.append(0)
for i in range(1, n+1):
phi[i] = i # indicates not evaluated yet
# and initializes for product
# formula.
# Compute other Phi values
for p in range(2,n+1):
# If phi[p] is not computed already,
# then number p is prime
if (phi[p] == p):
# Phi of a prime number p is
# always equal to p-1.
phi[p] = p-1
# Update phi values of all
# multiples of p
for i in range(2*p,n+1,p):
# Add contribution of p to its
# multiple i by multiplying with
# (1 - 1/p)
phi[i] = (phi[i]//p) * (p-1)
# Print precomputed phi values
for i in range(1,n+1):
print("Totient of ", i ," is ",
phi[i])
# Driver code
n = 12
computeTotient(n)
# This code is contributed
# by Anant Agarwal
C#
// C# program to check if given two
// strings are at distance one.
using System;
class GFG
{
// Computes and prints totient of all
// numbers smaller than or equal to n
static void computeTotient(int n)
{
// Create and initialize an array to
// store phi or totient values
long []phi = new long[n + 1];
for (int i = 1; i <= n; i++)
// indicates not evaluated yet
// and initializes for product
// formula.
phi[i] = i;
// Compute other Phi values
for (int p = 2; p <= n; p++)
{
// If phi[p] is not computed already,
// then number p is prime
if (phi[p] == p)
{
// Phi of a prime number p is
// always equal to p-1.
phi[p] = p - 1;
// Update phi values of all
// multiples of p
for (int i = 2 * p; i <= n; i += p)
{
// Add contribution of p to its
// multiple i by multiplying with
// (1 - 1/p)
phi[i] = (phi[i] / p) * (p - 1);
}
}
}
// Print precomputed phi values
for (int i = 1; i <= n; i++)
Console.WriteLine("Totient of " + i +" is " + phi[i]);
}
// Driver code
public static void Main()
{
int n = 12;
computeTotient(n);
}
}
// This code is contributed by Sam007.
PHP
<?php
// PHP program to compute Totient
// function for all numbers smaller
// than or equal to n.
// Computes and prints totient
// of all numbers smaller than
// or equal to n.
function computeTotient($n)
{
// Create and initialize
// an array to store
// phi or totient values
for($i = 1; $i <= $n; $i++)
// indicates not evaluated yet
// and initializes for product
// formula.
$phi[$i] = $i;
// Compute other Phi values
for($p = 2; $p <= $n; $p++)
{
// If phi[p] is not computed already,
// then number p is prime
if ($phi[$p] == $p)
{
// Phi of a prime number p is
// always equal to p-1.
$phi[$p] = $p - 1;
// Update phi values of all
// multiples of p
for($i = 2 * $p; $i <= $n; $i += $p)
{
// Add contribution of p to its
// multiple i by multiplying with
// (1 - 1/$p)
$phi[$i] = ($phi[$i] / $p) * ($p - 1);
}
}
}
// Print precomputed phi values
for($i = 1; $i <= $n; $i++)
echo "Totient of " , $i , " is ",
$phi[$i] ,"\n";
}
// Driver Code
$n = 12;
computeTotient($n);
// This code is contributed by ajit
?>
Javascript
<script>
// Javascript program to check if given two
// strings are at distance one.
// Computes and prints totient of all
// numbers smaller than or equal to n
function computeTotient(n)
{
// Create and initialize an array to
// store phi or totient values
let phi = new Array(n + 1);
for (let i = 1; i <= n; i++)
// indicates not evaluated yet
// and initializes for product
// formula.
phi[i] = i;
// Compute other Phi values
for (let p = 2; p <= n; p++)
{
// If phi[p] is not computed already,
// then number p is prime
if (phi[p] == p)
{
// Phi of a prime number p is
// always equal to p-1.
phi[p] = p - 1;
// Update phi values of all
// multiples of p
for (let i = 2 * p; i <= n; i += p)
{
// Add contribution of p to its
// multiple i by multiplying with
// (1 - 1/p)
phi[i] = parseInt(phi[i] / p, 10) * (p - 1);
}
}
}
// Print precomputed phi values
for (let i = 1; i <= n; i++)
document.write("Totient of " + i +" is " + phi[i] + "</br>");
}
let n = 12;
computeTotient(n);
</script>
Totient of 1 is 1 Totient of 2 is 1 Totient of 3 is 2 Totient of 4 is 2 Totient of 5 is 4 Totient of 6 is 2 Totient of 7 is 6 Totient of 8 is 4 Totient of 9 is 6 Totient of 10 is 4 Totient of 11 is 10 Totient of 12 is 4
La misma solución se puede usar cuando tenemos una gran cantidad de consultas para calcular la función totient.
Otra forma de calcular la función totient de Euler también se puede hacer usando la siguiente fórmula:
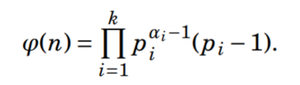
Función totient de Euler
Veamos un ejemplo para entender la función anterior, básicamente hace el mismo trabajo pero de forma diferente:
Por ejemplo, ϕ(12) = { (2^(2-1)) x (2-1) } x { (3^(1-1)) x (3-1) } =4
Tenga en cuenta que ϕ(n) = n−1 si n es primo.
A continuación se muestra la implementación de la fórmula anterior:
C++
// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
#define ll long long
ll Euler_totient_function(ll n)
{
ll result = 1;
for (ll i = 2; i * i <= n; i++) {
ll c = 0;
if (n % i == 0) {
while (n % i == 0) {
c++;
n /= i;
}
}
if (c > 0) {
ll power = (ll)pow(i, c - 1);
ll sm = (ll)pow(i, c - 1) * (i - 1);
result *= sm;
}
}
if (n > 1) {
result *= (n - 1);
}
return result;
}
// driver code
int main()
{
for (ll i = 1; i < 13; i++) {
cout << "Euler_totient_function(" << i << "): ";
cout << Euler_totient_function(i) << endl;
}
}
#praveeny182
Java
// Java program for the above approach
import java.io.*;
class GFG{
static long Euler_totient_function(long n)
{
long result = 1;
for(long i = 2; i * i <= n; i++)
{
long c = 0;
if (n % i == 0)
{
while (n % i == 0)
{
c++;
n /= i;
}
}
if (c > 0)
{
long power = (long)Math.pow(i, c - 1);
long sm = (long)Math.pow(i, c - 1) * (i - 1);
result *= sm;
}
}
if (n > 1)
{
result *= (n - 1);
}
return result;
}
// Driver code
public static void main(String[] args)
{
for(long i = 1; i < 13; i++)
{
System.out.print("Euler_totient_function(" +
i + "): ");
System.out.println(Euler_totient_function(i));
}
}
}
// This code is contributed by rishavmahato348
Python3
# python program for the above approach
import math
def Euler_totient_function(n):
result = 1
for i in range(2,n+1):
c = 0
if n % i == 0:
while (n % i == 0):
c+=1
n //= i
if (c > 0):
power = math.pow(i,c-1)
m = math.pow(i,c-1)*(i-1)
result*=m
if (n > 1):
result *= (n - 1)
return int(result)
for i in range(1,13):
print("Euler_totient_function(" , i , "): ",end="")
print(Euler_totient_function(i))
C#
// C# program for the above approach
using System;
class GFG {
static long Euler_totient_function(long n)
{
long result = 1;
for (long i = 2; i * i <= n; i++) {
long c = 0;
if (n % i == 0) {
while (n % i == 0) {
c++;
n /= i;
}
}
if (c > 0) {
long sm
= (long)Math.Pow(i, c - 1) * (i - 1);
result *= sm;
}
}
if (n > 1) {
result *= (n - 1);
}
return result;
}
// Driver code
public static void Main()
{
for (long i = 1; i < 13; i++) {
Console.Write("Euler_totient_function(" + i
+ "): ");
Console.WriteLine(Euler_totient_function(i));
}
}
}
// This code is contributed by rishavmahato348
Javascript
<script>
// Javascript program for the above approach
function Euler_totient_function(n)
{
let result = 1;
for (let i = 2; i * i <= n; i++) {
let c = 0;
if (n % i == 0) {
while (n % i == 0) {
c++;
n = parseInt(n / i);
}
}
if (c > 0) {
let power = Math.pow(i, c - 1);
let sm = Math.pow(i, c - 1) * (i - 1);
result *= sm;
}
}
if (n > 1) {
result *= (n - 1);
}
return result;
}
// driver code
for (let i = 1; i < 13; i++) {
document.write("Euler_totient_function(" + i + "): ");
document.write(Euler_totient_function(i) + "<br>");
}
// This code is contributed by subham348.
</script>
Euler_totient_function(1): 1 Euler_totient_function(2): 1 Euler_totient_function(3): 2 Euler_totient_function(4): 2 Euler_totient_function(5): 4 Euler_totient_function(6): 2 Euler_totient_function(7): 6 Euler_totient_function(8): 4 Euler_totient_function(9): 6 Euler_totient_function(10): 4 Euler_totient_function(11): 10 Euler_totient_function(12): 4
Este artículo es una contribución de Ekta Goel . Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA