Prerrequisitos: algoritmo Minimax en teoría de juegos , función de evaluación en teoría de juegos
La poda alfa-beta no es en realidad un algoritmo nuevo, sino una técnica de optimización para el algoritmo minimax. Reduce el tiempo de cálculo en un factor enorme. Esto nos permite buscar mucho más rápido e incluso adentrarnos en niveles más profundos en el árbol del juego. Corta ramas en el árbol del juego que no necesitan ser buscadas porque ya existe un mejor movimiento disponible. Se llama poda alfa-beta porque pasa 2 parámetros adicionales en la función minimax, a saber, alfa y beta.
Definamos los parámetros alfa y beta.
Alfa es el mejor valor que el maximizador actualmente puede garantizar en ese nivel o superior.
Betaes el mejor valor que el minimizador puede garantizar actualmente en ese nivel o superior.
Pseudocódigo:
function minimax(node, depth, isMaximizingPlayer, alpha, beta):
if node is a leaf node :
return value of the node
if isMaximizingPlayer :
bestVal = -INFINITY
for each child node :
value = minimax(node, depth+1, false, alpha, beta)
bestVal = max( bestVal, value)
alpha = max( alpha, bestVal)
if beta <= alpha:
break
return bestVal
else :
bestVal = +INFINITY
for each child node :
value = minimax(node, depth+1, true, alpha, beta)
bestVal = min( bestVal, value)
beta = min( beta, bestVal)
if beta <= alpha:
break
return bestVal
// Calling the function for the first time. minimax(0, 0, true, -INFINITY, +INFINITY)
Aclaremos el algoritmo anterior con un ejemplo.

- La llamada inicial comienza desde A . El valor de alfa aquí es -INFINITY y el valor de beta es +INFINITY . Estos valores se transmiten a los Nodes posteriores del árbol. En A , el maximizador debe elegir el máximo de B y C , por lo que A llama a B primero
- En B , el minimizador debe elegir min de D y E y, por lo tanto, llama a D primero.
- En D , mira a su hijo izquierdo, que es un Node de hoja. Este Node devuelve un valor de 3. Ahora el valor de alfa en D es max(-INF, 3) que es 3.
- Para decidir si vale la pena mirar su Node derecho o no, comprueba la condición beta<=alfa. Esto es falso ya que beta = +INF y alpha = 3. Entonces continúa la búsqueda.
- D ahora mira a su hijo derecho que devuelve un valor de 5. En D , alpha = max(3, 5) que es 5. Ahora el valor del Node D es 5
- D devuelve un valor de 5 a B . En B , beta = min( +INF, 5) que es 5. El minimizador ahora tiene garantizado un valor de 5 o menos. B ahora llama a E para ver si puede obtener un valor inferior a 5.
- En E , los valores de alfa y beta no son -INF y +INF, sino -INF y 5 respectivamente, porque el valor de beta se cambió en B y eso es lo que B pasó a E
- Ahora E mira a su hijo izquierdo que es 6. En E , alpha = max(-INF, 6) que es 6. Aquí la condición se vuelve verdadera. beta es 5 y alfa es 6. Así que beta<=alfa es verdadero. Por lo tanto se rompe y E devuelve 6 a B
- Nótese cómo no importa cuál sea el valor del hijo derecho de E. Podría haber sido +INF o -INF, igual no importaría. Ni siquiera tuvimos que mirarlo porque el minimizador tenía garantizado un valor de 5 o menos. Entonces, tan pronto como el maximizador vio el 6, supo que el minimizador nunca llegaría de esta manera porque puede obtener un 5 en el lado izquierdo de B . De esta manera, no tenemos que mirar ese 9 y, por lo tanto, ahorramos tiempo de cálculo.
- E devuelve un valor de 6 a B . En B , beta = min(5, 6) que es 5. El valor del Node B también es 5
Hasta ahora, así es como se ve nuestro árbol de juegos. El 9 está tachado porque nunca se calculó.

- B devuelve 5 a A. En A , alpha = max( -INF, 5) que es 5. Ahora el maximizador tiene garantizado un valor de 5 o mayor. A ahora llama a C para ver si puede obtener un valor superior a 5.
- En C , alfa = 5 y beta = +INF. C llama a F
- En F , alfa = 5 y beta = +INF. F mira a su hijo izquierdo, que es un 1. alfa = max (5, 1), que sigue siendo 5.
- F mira a su hijo derecho, que es un 2. Por lo tanto, el mejor valor de este Node es 2. Alfa sigue siendo 5
- F devuelve un valor de 2 a C . En C , beta = min( +INF, 2). La condición beta <= alfa se vuelve verdadera cuando beta = 2 y alfa = 5. Entonces se rompe y ni siquiera tiene que calcular todo el subárbol de G .
- La intuición detrás de esta ruptura es que, en C , al minimizador se le garantizó un valor de 2 o menos. Pero el maximizador ya tenía garantizado un valor de 5 si elegía B . Entonces, ¿por qué el maximizador elegiría C y obtendría un valor menor que 2? Una vez más, puede ver que no importaba cuáles fueran esos últimos 2 valores. También ahorramos muchos cálculos al omitir un subárbol completo.
- C ahora devuelve un valor de 2 a A . Por lo tanto, el mejor valor en A es max( 5, 2) que es 5.
- Por lo tanto, el valor óptimo que puede obtener el maximizador es 5
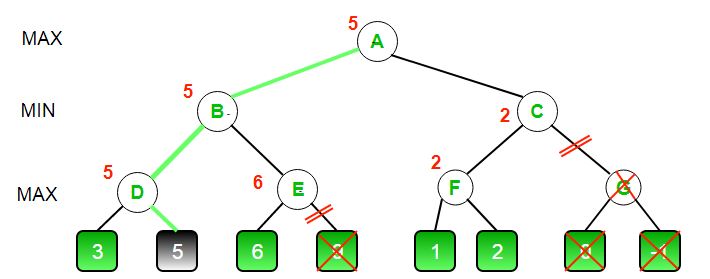
Así es como se ve nuestro árbol de juego final. Como puede ver, G se ha tachado porque nunca se calculó.
CPP
// C++ program to demonstrate
// working of Alpha-Beta Pruning
#include<bits/stdc++.h>
using namespace std;
// Initial values of
// Alpha and Beta
const int MAX = 1000;
const int MIN = -1000;
// Returns optimal value for
// current player(Initially called
// for root and maximizer)
int minimax(int depth, int nodeIndex,
bool maximizingPlayer,
int values[], int alpha,
int beta)
{
// Terminating condition. i.e
// leaf node is reached
if (depth == 3)
return values[nodeIndex];
if (maximizingPlayer)
{
int best = MIN;
// Recur for left and
// right children
for (int i = 0; i < 2; i++)
{
int val = minimax(depth + 1, nodeIndex * 2 + i,
false, values, alpha, beta);
best = max(best, val);
alpha = max(alpha, best);
// Alpha Beta Pruning
if (beta <= alpha)
break;
}
return best;
}
else
{
int best = MAX;
// Recur for left and
// right children
for (int i = 0; i < 2; i++)
{
int val = minimax(depth + 1, nodeIndex * 2 + i,
true, values, alpha, beta);
best = min(best, val);
beta = min(beta, best);
// Alpha Beta Pruning
if (beta <= alpha)
break;
}
return best;
}
}
// Driver Code
int main()
{
int values[8] = { 3, 5, 6, 9, 1, 2, 0, -1 };
cout <<"The optimal value is : "<< minimax(0, 0, true, values, MIN, MAX);;
return 0;
}
Java
// Java program to demonstrate
// working of Alpha-Beta Pruning
import java.io.*;
class GFG {
// Initial values of
// Alpha and Beta
static int MAX = 1000;
static int MIN = -1000;
// Returns optimal value for
// current player (Initially called
// for root and maximizer)
static int minimax(int depth, int nodeIndex,
Boolean maximizingPlayer,
int values[], int alpha,
int beta)
{
// Terminating condition. i.e
// leaf node is reached
if (depth == 3)
return values[nodeIndex];
if (maximizingPlayer)
{
int best = MIN;
// Recur for left and
// right children
for (int i = 0; i < 2; i++)
{
int val = minimax(depth + 1, nodeIndex * 2 + i,
false, values, alpha, beta);
best = Math.max(best, val);
alpha = Math.max(alpha, best);
// Alpha Beta Pruning
if (beta <= alpha)
break;
}
return best;
}
else
{
int best = MAX;
// Recur for left and
// right children
for (int i = 0; i < 2; i++)
{
int val = minimax(depth + 1, nodeIndex * 2 + i,
true, values, alpha, beta);
best = Math.min(best, val);
beta = Math.min(beta, best);
// Alpha Beta Pruning
if (beta <= alpha)
break;
}
return best;
}
}
// Driver Code
public static void main (String[] args)
{
int values[] = {3, 5, 6, 9, 1, 2, 0, -1};
System.out.println("The optimal value is : " +
minimax(0, 0, true, values, MIN, MAX));
}
}
// This code is contributed by vt_m.
Python3
# Python3 program to demonstrate
# working of Alpha-Beta Pruning
# Initial values of Alpha and Beta
MAX, MIN = 1000, -1000
# Returns optimal value for current player
#(Initially called for root and maximizer)
def minimax(depth, nodeIndex, maximizingPlayer,
values, alpha, beta):
# Terminating condition. i.e
# leaf node is reached
if depth == 3:
return values[nodeIndex]
if maximizingPlayer:
best = MIN
# Recur for left and right children
for i in range(0, 2):
val = minimax(depth + 1, nodeIndex * 2 + i,
False, values, alpha, beta)
best = max(best, val)
alpha = max(alpha, best)
# Alpha Beta Pruning
if beta <= alpha:
break
return best
else:
best = MAX
# Recur for left and
# right children
for i in range(0, 2):
val = minimax(depth + 1, nodeIndex * 2 + i,
True, values, alpha, beta)
best = min(best, val)
beta = min(beta, best)
# Alpha Beta Pruning
if beta <= alpha:
break
return best
# Driver Code
if __name__ == "__main__":
values = [3, 5, 6, 9, 1, 2, 0, -1]
print("The optimal value is :", minimax(0, 0, True, values, MIN, MAX))
# This code is contributed by Rituraj Jain
C#
// C# program to demonstrate
// working of Alpha-Beta Pruning
using System;
class GFG
{
// Initial values of
// Alpha and Beta
static int MAX = 1000;
static int MIN = -1000;
// Returns optimal value for
// current player (Initially called
// for root and maximizer)
static int minimax(int depth, int nodeIndex,
Boolean maximizingPlayer,
int []values, int alpha,
int beta)
{
// Terminating condition. i.e
// leaf node is reached
if (depth == 3)
return values[nodeIndex];
if (maximizingPlayer)
{
int best = MIN;
// Recur for left and
// right children
for (int i = 0; i < 2; i++)
{
int val = minimax(depth + 1, nodeIndex * 2 + i,
false, values, alpha, beta);
best = Math.Max(best, val);
alpha = Math.Max(alpha, best);
// Alpha Beta Pruning
if (beta <= alpha)
break;
}
return best;
}
else
{
int best = MAX;
// Recur for left and
// right children
for (int i = 0; i < 2; i++)
{
int val = minimax(depth + 1, nodeIndex * 2 + i,
true, values, alpha, beta);
best = Math.Min(best, val);
beta = Math.Min(beta, best);
// Alpha Beta Pruning
if (beta <= alpha)
break;
}
return best;
}
}
// Driver Code
public static void Main (String[] args)
{
int []values = {3, 5, 6, 9, 1, 2, 0, -1};
Console.WriteLine("The optimal value is : " +
minimax(0, 0, true, values, MIN, MAX));
}
}
// This code is contributed by 29AjayKumar
Javascript
<script>
// Javascript program to demonstrate
// working of Alpha-Beta Pruning
// Initial values of
// Alpha and Beta
let MAX = 1000;
let MIN = -1000;
// Returns optimal value for
// current player (Initially called
// for root and maximizer)
function minimax(depth,nodeIndex,maximizingPlayer,values,alpha,beta)
{
// Terminating condition. i.e
// leaf node is reached
if (depth == 3)
return values[nodeIndex];
if (maximizingPlayer)
{
let best = MIN;
// Recur for left and
// right children
for (let i = 0; i < 2; i++)
{
let val = minimax(depth + 1, nodeIndex * 2 + i,
false, values, alpha, beta);
best = Math.max(best, val);
alpha = Math.max(alpha, best);
// Alpha Beta Pruning
if (beta <= alpha)
break;
}
return best;
}
else
{
let best = MAX;
// Recur for left and
// right children
for (let i = 0; i < 2; i++)
{
let val = minimax(depth + 1, nodeIndex * 2 + i,
true, values, alpha, beta);
best = Math.min(best, val);
beta = Math.min(beta, best);
// Alpha Beta Pruning
if (beta <= alpha)
break;
}
return best;
}
}
// Driver Code
let values=[3, 5, 6, 9, 1, 2, 0, -1];
document.write("The optimal value is : " +
minimax(0, 0, true, values, MIN, MAX));
// This code is contributed by rag2127
</script>
Producción :
The optimal value is : 5
Este artículo es una contribución de Akshay L Aradhya . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA