Análisis de Algoritmos | Análisis O grande

En nuestros artículos anteriores sobre Análisis de Algoritmos , habíamos discutido brevemente las notaciones asintóticas, su desempeño en el mejor y el peor de los casos, etc. En este artículo, discutimos el análisis del algoritmo utilizando la notación asintótica Big – O en completo detalle. 
 Análisis Big-O de algoritmos

Podemos expresar la complejidad algorítmica usando la notación O grande. Para un problema de tamaño N:

• Una función/método de tiempo constante es «orden 1»: O(1)
• Una función/método de tiempo lineal es “orden N”: O(N)
• Una función/método de tiempo cuadrático es “orden N al cuadrado”: ​​O(N 2 )

Definición: Sean g y f funciones del conjunto de los números naturales a sí mismo. Se dice que la función f es O(g) (léase gran-oh de g), si hay una constante c > 0 y un número natural n ₀ tal que f (n) ≤ cg(n) para todo n >= n ₀ .

Nota: ¡O(g) es un conjunto!

Abuso de notación: f = O(g) no significa f ∈ O(g).
La notación asintótica Big-O nos da la idea de límite superior, matemáticamente descrita a continuación: 

f(n) = O(g(n)) si existe un entero positivo n ₀ y una constante positiva c, tal que f(n)≤cg(n) ∀ n≥n ₀ 

El procedimiento paso a paso general para el análisis de tiempo de ejecución Big-O es el siguiente:  

1. Averigüe cuál es la entrada y qué representa n.
2. Exprese el número máximo de operaciones que realiza el algoritmo en términos de n.
3. Elimine todos excepto los términos de mayor orden.
4. Elimina todos los factores constantes.

Algunas de las propiedades útiles del análisis de notación Big-O son las siguientes: 

▪ Multiplicación Constante: 
Si f(n) = cg(n), entonces O(f(n)) = O(g(n)) ; donde c es una constante distinta de cero. 
▪ Función Polinomial: 
Si f(n) = a ₀ + a ₁ .n + a ₂ .n ² + —- + a _m .n ^m , entonces O(f(n)) = O(n ^m ). 
▪ Función sumatoria: 
Si f(n) = f ₁ (n) + f ₂ (n) + —- + f _m (n) y f _i (n)≤f _i+1 (n) ∀ i=1, 2 , —-, m, 
entonces O(f(n)) = O(max(f ₁ (n), f ₂ (n), —-, f _m (n))). 
▪ Función Logarítmica: 
Si f(n) = log _a n y g(n)=log _b n, entonces O(f(n))=O(g(n)) 
; todas las funciones de registro crecen de la misma manera en términos de Big-O.

 Básicamente, esta notación asintótica se utiliza para medir y comparar teóricamente los peores escenarios de los algoritmos. Para cualquier algoritmo, el análisis Big-O debería ser sencillo siempre que identifiquemos correctamente las operaciones que dependen de n, el tamaño de entrada. 
Análisis de tiempo de ejecución de algoritmos

En casos generales, utilizamos principalmente para medir y comparar las complejidades teóricas del tiempo de ejecución del peor de los casos de los algoritmos para el análisis de rendimiento. 
El tiempo de ejecución más rápido posible para cualquier algoritmo es O(1), comúnmente denominado Tiempo de ejecución constante . En este caso, el algoritmo siempre tarda la misma cantidad de tiempo en ejecutarse, independientemente del tamaño de entrada. Este es el tiempo de ejecución ideal para un algoritmo, pero rara vez se puede lograr. 
En casos reales, el rendimiento (Tiempo de ejecución) de un algoritmo depende de n, es decir, el tamaño de la entrada o el número de operaciones necesarias para cada elemento de entrada. 
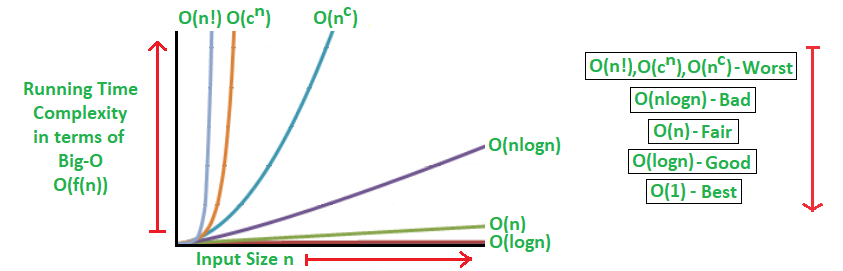
Los algoritmos se pueden clasificar de la siguiente manera, de mejor a peor rendimiento (complejidad del tiempo de ejecución): 

▪ Un algoritmo logarítmico – O(logn) 
Runtime crece logarítmicamente en proporción a n. 
▪ Un algoritmo lineal: O(n) 
Runtime crece directamente en proporción a n. 
▪ Un algoritmo superlineal – O(nlogn) 
Runtime crece en proporción a n. 
▪ Un algoritmo polinomial – O(n ^c )  El
tiempo de ejecución crece más rápido que el anterior, todo basado en n. 
▪ Un algoritmo exponencial – O(c ⁿ )  El
tiempo de ejecución crece aún más rápido que el algoritmo polinomial basado en n. 
▪ Un algoritmo factorial – O(n!) 
Runtime crece más rápido y se vuelve rápidamente inutilizable incluso para 
valores pequeños de n.  

Donde, n es el tamaño de entrada y c es una constante positiva. 
 

Ejemplos algorítmicos de análisis de tiempo de ejecución : 
algunos de los ejemplos de todos esos tipos de algoritmos (en los peores escenarios) se mencionan a continuación: 

▪ Algoritmo logarítmico – O(logn) – Búsqueda binaria. 
▪ Algoritmo lineal – O(n) – Búsqueda lineal. 
▪ Algoritmo superlineal – O(nlogn) – Heap Sort, Merge Sort. 
▪ Algoritmo polinomial – O(n^c) – Multiplicación de array de Strassen, Clasificación de burbuja, Clasificación de selección, Clasificación de inserción, Clasificación de cubeta. 
▪ Algoritmo exponencial – O(c^n) – Torre de Hanoi. 
▪ Algoritmo Factorial – O(n!) – Expansión de Determinantes por Menores, Algoritmo de Búsqueda de Fuerza Bruta para el Problema del Viajante. 

Ejemplos matemáticos de análisis de tiempo de ejecución : 
las actuaciones (tiempos de ejecución) de diferentes órdenes de algoritmos se separan rápidamente a medida que n (el tamaño de entrada) se hace más grande. Consideremos el ejemplo matemático:  

If n = 10,                  If n=20,
    log(10) = 1;                log(20) = 2.996;
    10 = 10;                    20 = 20;
    10log(10)=10;               20log(20)=59.9;
    102=100;                    202=400;
    210=1024;                    220=1048576;
    10!=3628800;                20!=2.432902e+1818;

Análisis de Huella de Memoria de Algoritmos

Para el análisis de rendimiento de un algoritmo, la medición del tiempo de ejecución no solo es una métrica relevante, sino que también debemos considerar la cantidad de uso de memoria del programa. Esto se conoce como la Huella de memoria del algoritmo, conocida en breve como Complejidad espacial. 
Aquí también, necesitamos medir y comparar las complejidades espaciales teóricas de los algoritmos en el peor de los casos para el análisis de rendimiento. 
Básicamente depende de dos grandes aspectos que se describen a continuación: 

• En primer lugar, la implementación del programa es responsable del uso de la memoria. Por ejemplo, podemos suponer que la implementación recursiva siempre reserva más memoria que la implementación iterativa correspondiente de un problema en particular.
• Y el otro es n, el tamaño de entrada o la cantidad de almacenamiento requerida para cada elemento. Por ejemplo, un algoritmo simple con una gran cantidad de tamaño de entrada puede consumir más memoria que un algoritmo complejo con una cantidad menor de tamaño de entrada.

Ejemplos algorítmicos de análisis de huella de memoria: los algoritmos con ejemplos se clasifican de mejor a peor rendimiento (complejidad espacial) en función de los peores escenarios que se mencionan a continuación:  

▪ Ideal algorithm - O(1) - Linear Search, Binary Search,
    Bubble Sort, Selection Sort, Insertion Sort, Heap Sort, Shell Sort.
▪ Logarithmic algorithm - O(log n) - Merge Sort.
▪ Linear algorithm - O(n) - Quick Sort.
▪ Sub-linear algorithm - O(n+k) - Radix Sort.

Compensación espacio-tiempo y eficiencia

Por lo general, existe una compensación entre el uso óptimo de la memoria y el rendimiento del tiempo de ejecución. 
En general, para un algoritmo, la eficiencia de espacio y la eficiencia de tiempo llegan a dos extremos opuestos y cada punto entre ellos tiene una cierta eficiencia de tiempo y espacio. Entonces, mientras más eficiencia de tiempo tengas, menos eficiencia de espacio tendrás y viceversa. 
Por ejemplo, el algoritmo Mergesort es extremadamente rápido pero requiere mucho espacio para realizar las operaciones. Por otro lado, Bubble Sort es extremadamente lento pero requiere el mínimo espacio. 
Al final de este tema, podemos concluir que encontrar un algoritmo que funcione en menos tiempo de ejecución y que también tenga menos requisitos de espacio de memoria puede marcar una gran diferencia en el rendimiento de un algoritmo.

Ejemplo de notación Big-oh:

// C++ program to findtime complexity for single for loop
#include <bits/stdc++.h>
using namespace std;
// main Code
int main()
{
              //declare variable
    int a = 0, b = 0;
              //declare size 
    int N = 5, M = 5;
    // This loop runs for N time
    for (int i = 0; i < N; i++) {
        a = a + 5;
    }
    // This loop runs for M time
    for (int i = 0; i < M; i++) {
        b = b + 10;
    }
   //print value of a and b
    cout << a << ' ' << b;
    return 0;
}

25 50

Explicación: 
el primer ciclo ejecuta N tiempo mientras que el segundo ciclo ejecuta M tiempo. El cálculo toma O(1)veces .
Entonces, al sumarlos, la complejidad del tiempo será O ( N + M + 1) = O ( N + M).

Complejidad de tiempo : O (N + M)

Para más detalles, consulte:
Diseño y Análisis de Algoritmos .