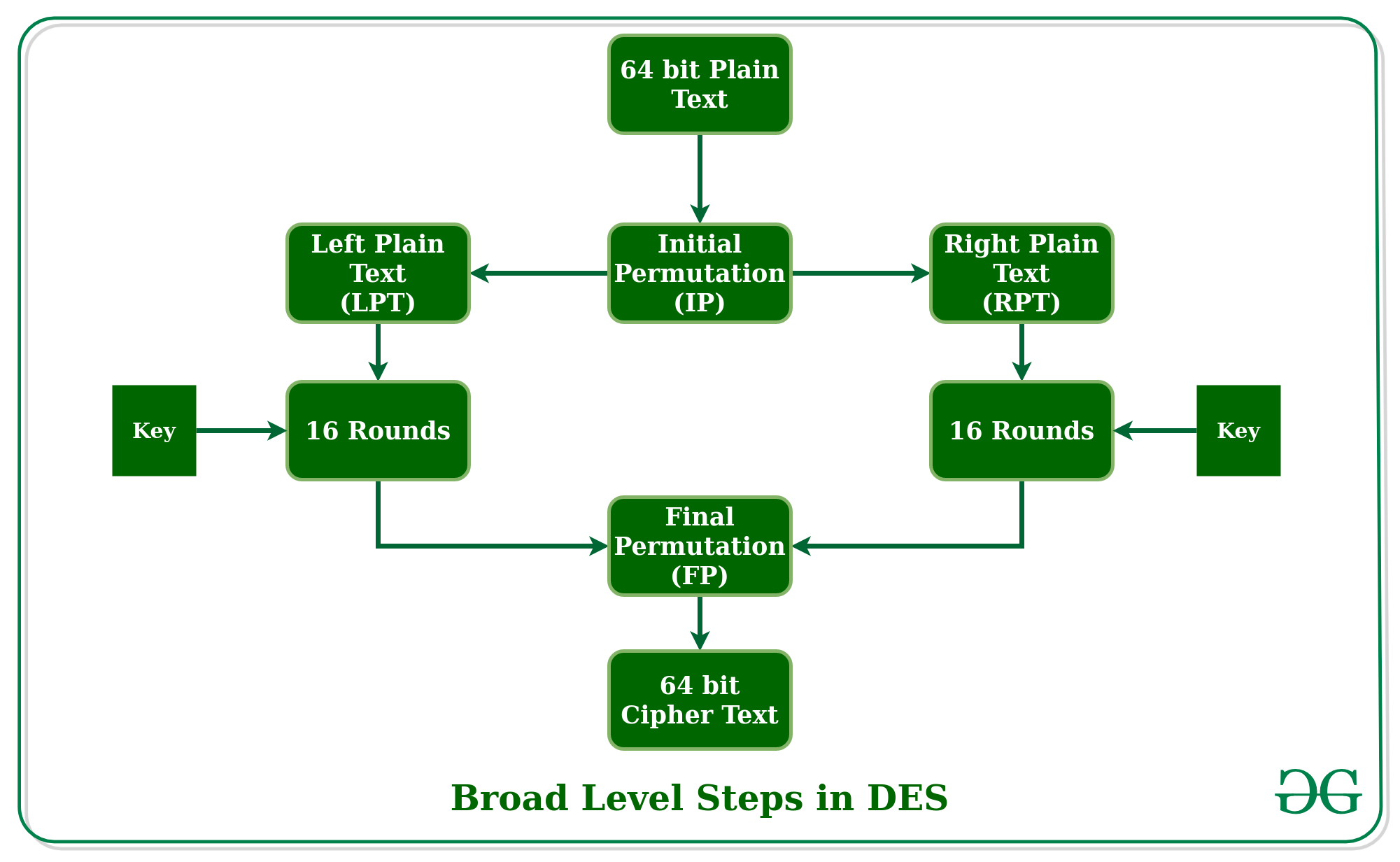
El estándar de cifrado de datos (DES) se ha encontrado vulnerable a ataques muy poderosos y, por lo tanto, la popularidad de DES se ha encontrado ligeramente en declive. DES es un cifrado de bloque y cifra los datos en bloques de 64 bits cada uno, lo que significa que 64 bits de texto sin formato van como entrada a DES, que produce 64 bits de texto cifrado. El mismo algoritmo y clave se utilizan para el cifrado y descifrado, con pequeñas diferencias. La longitud de la clave es de 56 bits. La idea básica se muestra en la figura.

Hemos mencionado que DES usa una clave de 56 bits. En realidad, la clave inicial consta de 64 bits. Sin embargo, incluso antes de que comience el proceso DES, cada octavo bit de la clave se descarta para producir una clave de 56 bits. Es decir, las posiciones de bits 8, 16, 24, 32, 40, 48, 56 y 64 se descartan.

Por lo tanto, el descarte de cada 8 bits de la clave produce una clave de 56 bits a partir de la clave original de 64 bits.
DES se basa en los dos atributos fundamentales de la criptografía: sustitución (también llamada confusión) y transposición (también llamada difusión). DES consta de 16 pasos, cada uno de los cuales se denomina ronda. Cada ronda realiza los pasos de sustitución y transposición. Analicemos ahora los pasos de nivel amplio en DES.
- En el primer paso, el bloque de texto sin formato de 64 bits se transfiere a una función de permutación (IP) inicial.
- La permutación inicial se realiza en texto sin formato.
- Luego, la permutación inicial (IP) produce dos mitades del bloque permutado; diciendo Texto sin formato a la izquierda (LPT) y Texto sin formato a la derecha (RPT).
- Ahora, cada LPT y RPT pasan por 16 rondas del proceso de encriptación.
- Al final, LPT y RPT se vuelven a unir y se realiza una permutación final (FP) en el bloque combinado
- El resultado de este proceso produce texto cifrado de 64 bits.
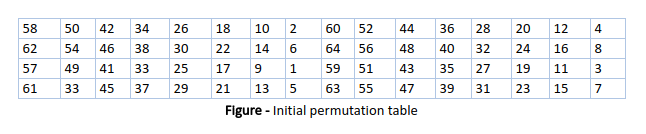
Permutación inicial (IP): como hemos señalado, la permutación inicial (IP) ocurre solo una vez y ocurre antes de la primera ronda. Sugiere cómo debe proceder la transposición en IP, como se muestra en la figura. Por ejemplo, dice que la IP reemplaza el primer bit del bloque de texto sin formato original con el bit 58 del texto sin formato original, el segundo bit con el bit 50 del bloque de texto sin formato original, y así sucesivamente.
Esto no es más que malabarismo de posiciones de bits del bloque de texto sin formato original. la misma regla se aplica a todas las demás posiciones de bits que se muestran en la figura.
Como hemos señalado, una vez finalizada la IP, el bloque de texto permutado de 64 bits resultante se divide en dos medios bloques. Cada medio bloque consta de 32 bits, y cada una de las 16 rondas, a su vez, consta de los pasos de nivel amplio que se describen en la figura.

Paso 1: Transformación de clave: Hemos notado que la clave inicial de 64 bits se transforma en una clave de 56 bits descartando cada 8 bits de la clave inicial. Por lo tanto, para cada uno hay disponible una clave de 56 bits. A partir de esta clave de 56 bits, se genera una subclave diferente de 48 bits durante cada ronda mediante un proceso llamado transformación de clave. Para ello, la clave de 56 bits se divide en dos mitades, cada una de 28 bits. Estas mitades se desplazan circularmente hacia la izquierda una o dos posiciones, según la ronda.
Por ejemplo, si los números de ronda 1, 2, 9 o 16, el cambio se realiza en una sola posición para las otras rondas, el cambio circular se realiza en dos posiciones. El número de bits de llave desplazados por ronda se muestra en la figura.

Después de un cambio apropiado, se seleccionan 48 de los 56 bits. para seleccionar 48 de los 56 bits, la tabla se muestra en la figura siguiente. Por ejemplo, después del cambio, el bit número 14 se mueve a la primera posición, el bit número 17 se mueve a la segunda posición y así sucesivamente. Si observamos la tabla detenidamente, nos daremos cuenta de que contiene solo posiciones de 48 bits. Se descarta el bit número 18 (no lo encontraremos en la tabla), como otros 7, para reducir una clave de 56 bits a una clave de 48 bits. Dado que el proceso de transformación de clave implica permutación, así como una selección de un subconjunto de 48 bits de la clave original de 56 bits, se denomina permutación de compresión.

Debido a esta técnica de permutación de compresión, se utiliza un subconjunto diferente de bits clave en cada ronda. Eso hace que DES no sea fácil de descifrar.
Paso 2: Permutación de expansión: recuerde que después de la permutación inicial, teníamos dos áreas de texto sin formato de 32 bits llamadas Texto sin formato izquierdo (LPT) y Texto sin formato derecho (RPT). Durante la permutación de expansión, el RPT se expande de 32 bits a 48 bits. Los bits también se permutan, por lo que se denomina permutación de expansión. Esto sucede cuando el RPT de 32 bits se divide en 8 bloques, y cada bloque consta de 4 bits. Luego, cada bloque de 4 bits del paso anterior se expande a un bloque de 6 bits correspondiente, es decir, por bloque de 4 bits, se agregan 2 bits más.

Este proceso da como resultado una expansión y una permutación del bit de entrada mientras se crea la salida. El proceso de transformación de clave comprime la clave de 56 bits a 48 bits. Luego, el proceso de permutación de expansión expande el RPT de 32 bits a 48 bits. Ahora, la clave de 48 bits es XOR con RPT de 48 bits y la salida resultante pasa al siguiente paso, que es la sustitución de S-Box.
C++
#include <bits/stdc++.h>
using namespace std;
string hex2bin(string s)
{
// hexadecimal to binary conversion
unordered_map<char, string> mp;
mp['0'] = "0000";
mp['1'] = "0001";
mp['2'] = "0010";
mp['3'] = "0011";
mp['4'] = "0100";
mp['5'] = "0101";
mp['6'] = "0110";
mp['7'] = "0111";
mp['8'] = "1000";
mp['9'] = "1001";
mp['A'] = "1010";
mp['B'] = "1011";
mp['C'] = "1100";
mp['D'] = "1101";
mp['E'] = "1110";
mp['F'] = "1111";
string bin = "";
for (int i = 0; i < s.size(); i++) {
bin += mp[s[i]];
}
return bin;
}
string bin2hex(string s)
{
// binary to hexadecimal conversion
unordered_map<string, string> mp;
mp["0000"] = "0";
mp["0001"] = "1";
mp["0010"] = "2";
mp["0011"] = "3";
mp["0100"] = "4";
mp["0101"] = "5";
mp["0110"] = "6";
mp["0111"] = "7";
mp["1000"] = "8";
mp["1001"] = "9";
mp["1010"] = "A";
mp["1011"] = "B";
mp["1100"] = "C";
mp["1101"] = "D";
mp["1110"] = "E";
mp["1111"] = "F";
string hex = "";
for (int i = 0; i < s.length(); i += 4) {
string ch = "";
ch += s[i];
ch += s[i + 1];
ch += s[i + 2];
ch += s[i + 3];
hex += mp[ch];
}
return hex;
}
string permute(string k, int* arr, int n)
{
string per = "";
for (int i = 0; i < n; i++) {
per += k[arr[i] - 1];
}
return per;
}
string shift_left(string k, int shifts)
{
string s = "";
for (int i = 0; i < shifts; i++) {
for (int j = 1; j < 28; j++) {
s += k[j];
}
s += k[0];
k = s;
s = "";
}
return k;
}
string xor_(string a, string b)
{
string ans = "";
for (int i = 0; i < a.size(); i++) {
if (a[i] == b[i]) {
ans += "0";
}
else {
ans += "1";
}
}
return ans;
}
string encrypt(string pt, vector<string> rkb, vector<string> rk)
{
// Hexadecimal to binary
pt = hex2bin(pt);
// Initial Permutation Table
int initial_perm[64] = { 58, 50, 42, 34, 26, 18, 10, 2,
60, 52, 44, 36, 28, 20, 12, 4,
62, 54, 46, 38, 30, 22, 14, 6,
64, 56, 48, 40, 32, 24, 16, 8,
57, 49, 41, 33, 25, 17, 9, 1,
59, 51, 43, 35, 27, 19, 11, 3,
61, 53, 45, 37, 29, 21, 13, 5,
63, 55, 47, 39, 31, 23, 15, 7 };
// Initial Permutation
pt = permute(pt, initial_perm, 64);
cout << "After initial permutation: " << bin2hex(pt) << endl;
// Splitting
string left = pt.substr(0, 32);
string right = pt.substr(32, 32);
cout << "After splitting: L0=" << bin2hex(left)
<< " R0=" << bin2hex(right) << endl;
// Expansion D-box Table
int exp_d[48] = { 32, 1, 2, 3, 4, 5, 4, 5,
6, 7, 8, 9, 8, 9, 10, 11,
12, 13, 12, 13, 14, 15, 16, 17,
16, 17, 18, 19, 20, 21, 20, 21,
22, 23, 24, 25, 24, 25, 26, 27,
28, 29, 28, 29, 30, 31, 32, 1 };
// S-box Table
int s[8][4][16] = { { 14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7,
0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8,
4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0,
15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13 },
{ 15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10,
3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5,
0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15,
13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9 },
{ 10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8,
13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1,
13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7,
1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12 },
{ 7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15,
13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9,
10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4,
3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14 },
{ 2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9,
14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6,
4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14,
11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3 },
{ 12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11,
10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8,
9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6,
4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13 },
{ 4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1,
13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6,
1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2,
6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12 },
{ 13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7,
1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2,
7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8,
2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11 } };
// Straight Permutation Table
int per[32] = { 16, 7, 20, 21,
29, 12, 28, 17,
1, 15, 23, 26,
5, 18, 31, 10,
2, 8, 24, 14,
32, 27, 3, 9,
19, 13, 30, 6,
22, 11, 4, 25 };
cout << endl;
for (int i = 0; i < 16; i++) {
// Expansion D-box
string right_expanded = permute(right, exp_d, 48);
// XOR RoundKey[i] and right_expanded
string x = xor_(rkb[i], right_expanded);
// S-boxes
string op = "";
for (int i = 0; i < 8; i++) {
int row = 2 * int(x[i * 6] - '0') + int(x[i * 6 + 5] - '0');
int col = 8 * int(x[i * 6 + 1] - '0') + 4 * int(x[i * 6 + 2] - '0') + 2 * int(x[i * 6 + 3] - '0') + int(x[i * 6 + 4] - '0');
int val = s[i][row][col];
op += char(val / 8 + '0');
val = val % 8;
op += char(val / 4 + '0');
val = val % 4;
op += char(val / 2 + '0');
val = val % 2;
op += char(val + '0');
}
// Straight D-box
op = permute(op, per, 32);
// XOR left and op
x = xor_(op, left);
left = x;
// Swapper
if (i != 15) {
swap(left, right);
}
cout << "Round " << i + 1 << " " << bin2hex(left) << " "
<< bin2hex(right) << " " << rk[i] << endl;
}
// Combination
string combine = left + right;
// Final Permutation Table
int final_perm[64] = { 40, 8, 48, 16, 56, 24, 64, 32,
39, 7, 47, 15, 55, 23, 63, 31,
38, 6, 46, 14, 54, 22, 62, 30,
37, 5, 45, 13, 53, 21, 61, 29,
36, 4, 44, 12, 52, 20, 60, 28,
35, 3, 43, 11, 51, 19, 59, 27,
34, 2, 42, 10, 50, 18, 58, 26,
33, 1, 41, 9, 49, 17, 57, 25 };
// Final Permutation
string cipher = bin2hex(permute(combine, final_perm, 64));
return cipher;
}
int main()
{
// pt is plain text
string pt, key;
/*cout<<"Enter plain text(in hexadecimal): ";
cin>>pt;
cout<<"Enter key(in hexadecimal): ";
cin>>key;*/
pt = "123456ABCD132536";
key = "AABB09182736CCDD";
// Key Generation
// Hex to binary
key = hex2bin(key);
// Parity bit drop table
int keyp[56] = { 57, 49, 41, 33, 25, 17, 9,
1, 58, 50, 42, 34, 26, 18,
10, 2, 59, 51, 43, 35, 27,
19, 11, 3, 60, 52, 44, 36,
63, 55, 47, 39, 31, 23, 15,
7, 62, 54, 46, 38, 30, 22,
14, 6, 61, 53, 45, 37, 29,
21, 13, 5, 28, 20, 12, 4 };
// getting 56 bit key from 64 bit using the parity bits
key = permute(key, keyp, 56); // key without parity
// Number of bit shifts
int shift_table[16] = { 1, 1, 2, 2,
2, 2, 2, 2,
1, 2, 2, 2,
2, 2, 2, 1 };
// Key- Compression Table
int key_comp[48] = { 14, 17, 11, 24, 1, 5,
3, 28, 15, 6, 21, 10,
23, 19, 12, 4, 26, 8,
16, 7, 27, 20, 13, 2,
41, 52, 31, 37, 47, 55,
30, 40, 51, 45, 33, 48,
44, 49, 39, 56, 34, 53,
46, 42, 50, 36, 29, 32 };
// Splitting
string left = key.substr(0, 28);
string right = key.substr(28, 28);
vector<string> rkb; // rkb for RoundKeys in binary
vector<string> rk; // rk for RoundKeys in hexadecimal
for (int i = 0; i < 16; i++) {
// Shifting
left = shift_left(left, shift_table[i]);
right = shift_left(right, shift_table[i]);
// Combining
string combine = left + right;
// Key Compression
string RoundKey = permute(combine, key_comp, 48);
rkb.push_back(RoundKey);
rk.push_back(bin2hex(RoundKey));
}
cout << "\nEncryption:\n\n";
string cipher = encrypt(pt, rkb, rk);
cout << "\nCipher Text: " << cipher << endl;
cout << "\nDecryption\n\n";
reverse(rkb.begin(), rkb.end());
reverse(rk.begin(), rk.end());
string text = encrypt(cipher, rkb, rk);
cout << "\nPlain Text: " << text << endl;
}
Java
import java.util.*;
class Main {
private static class DES {
// CONSTANTS
// Initial Permutation Table
int[] IP = { 58, 50, 42, 34, 26, 18,
10, 2, 60, 52, 44, 36, 28, 20,
12, 4, 62, 54, 46, 38,
30, 22, 14, 6, 64, 56,
48, 40, 32, 24, 16, 8,
57, 49, 41, 33, 25, 17,
9, 1, 59, 51, 43, 35, 27,
19, 11, 3, 61, 53, 45,
37, 29, 21, 13, 5, 63, 55,
47, 39, 31, 23, 15, 7 };
// Inverse Initial Permutation Table
int[] IP1 = { 40, 8, 48, 16, 56, 24, 64,
32, 39, 7, 47, 15, 55,
23, 63, 31, 38, 6, 46,
14, 54, 22, 62, 30, 37,
5, 45, 13, 53, 21, 61,
29, 36, 4, 44, 12, 52,
20, 60, 28, 35, 3, 43,
11, 51, 19, 59, 27, 34,
2, 42, 10, 50, 18, 58,
26, 33, 1, 41, 9, 49,
17, 57, 25 };
// first key-hePermutation Table
int[] PC1 = { 57, 49, 41, 33, 25,
17, 9, 1, 58, 50, 42, 34, 26,
18, 10, 2, 59, 51, 43, 35, 27,
19, 11, 3, 60, 52, 44, 36, 63,
55, 47, 39, 31, 23, 15, 7, 62,
54, 46, 38, 30, 22, 14, 6, 61,
53, 45, 37, 29, 21, 13, 5, 28,
20, 12, 4 };
// second key-Permutation Table
int[] PC2 = { 14, 17, 11, 24, 1, 5, 3,
28, 15, 6, 21, 10, 23, 19, 12,
4, 26, 8, 16, 7, 27, 20, 13, 2,
41, 52, 31, 37, 47, 55, 30, 40,
51, 45, 33, 48, 44, 49, 39, 56,
34, 53, 46, 42, 50, 36, 29, 32 };
// Expansion D-box Table
int[] EP = { 32, 1, 2, 3, 4, 5, 4,
5, 6, 7, 8, 9, 8, 9, 10,
11, 12, 13, 12, 13, 14, 15,
16, 17, 16, 17, 18, 19, 20,
21, 20, 21, 22, 23, 24, 25,
24, 25, 26, 27, 28, 29, 28,
29, 30, 31, 32, 1 };
// Straight Permutation Table
int[] P = { 16, 7, 20, 21, 29, 12, 28,
17, 1, 15, 23, 26, 5, 18,
31, 10, 2, 8, 24, 14, 32,
27, 3, 9, 19, 13, 30, 6,
22, 11, 4, 25 };
// S-box Table
int[][][] sbox = {
{ { 14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7 },
{ 0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8 },
{ 4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0 },
{ 15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13 } },
{ { 15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10 },
{ 3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5 },
{ 0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15 },
{ 13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9 } },
{ { 10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8 },
{ 13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1 },
{ 13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7 },
{ 1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12 } },
{ { 7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15 },
{ 13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9 },
{ 10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4 },
{ 3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14 } },
{ { 2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9 },
{ 14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6 },
{ 4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14 },
{ 11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3 } },
{ { 12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11 },
{ 10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8 },
{ 9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6 },
{ 4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13 } },
{ { 4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1 },
{ 13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6 },
{ 1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2 },
{ 6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12 } },
{ { 13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7 },
{ 1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2 },
{ 7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8 },
{ 2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11 } }
};
int[] shiftBits = { 1, 1, 2, 2, 2, 2, 2, 2,
1, 2, 2, 2, 2, 2, 2, 1 };
// hexadecimal to binary conversion
String hextoBin(String input)
{
int n = input.length() * 4;
input = Long.toBinaryString(
Long.parseUnsignedLong(input, 16));
while (input.length() < n)
input = "0" + input;
return input;
}
// binary to hexadecimal conversion
String binToHex(String input)
{
int n = (int)input.length() / 4;
input = Long.toHexString(
Long.parseUnsignedLong(input, 2));
while (input.length() < n)
input = "0" + input;
return input;
}
// per-mutate input hexadecimal
// according to specified sequence
String permutation(int[] sequence, String input)
{
String output = "";
input = hextoBin(input);
for (int i = 0; i < sequence.length; i++)
output += input.charAt(sequence[i] - 1);
output = binToHex(output);
return output;
}
// xor 2 hexadecimal strings
String xor(String a, String b)
{
// hexadecimal to decimal(base 10)
long t_a = Long.parseUnsignedLong(a, 16);
// hexadecimal to decimal(base 10)
long t_b = Long.parseUnsignedLong(b, 16);
// xor
t_a = t_a ^ t_b;
// decimal to hexadecimal
a = Long.toHexString(t_a);
// prepend 0's to maintain length
while (a.length() < b.length())
a = "0" + a;
return a;
}
// left Circular Shifting bits
String leftCircularShift(String input, int numBits)
{
int n = input.length() * 4;
int perm[] = new int[n];
for (int i = 0; i < n - 1; i++)
perm[i] = (i + 2);
perm[n - 1] = 1;
while (numBits-- > 0)
input = permutation(perm, input);
return input;
}
// preparing 16 keys for 16 rounds
String[] getKeys(String key)
{
String keys[] = new String[16];
// first key permutation
key = permutation(PC1, key);
for (int i = 0; i < 16; i++) {
key = leftCircularShift(
key.substring(0, 7), shiftBits[i])
+ leftCircularShift(key.substring(7, 14),
shiftBits[i]);
// second key permutation
keys[i] = permutation(PC2, key);
}
return keys;
}
// s-box lookup
String sBox(String input)
{
String output = "";
input = hextoBin(input);
for (int i = 0; i < 48; i += 6) {
String temp = input.substring(i, i + 6);
int num = i / 6;
int row = Integer.parseInt(
temp.charAt(0) + "" + temp.charAt(5), 2);
int col = Integer.parseInt(
temp.substring(1, 5), 2);
output += Integer.toHexString(
sbox[num][row][col]);
}
return output;
}
String round(String input, String key, int num)
{
// fk
String left = input.substring(0, 8);
String temp = input.substring(8, 16);
String right = temp;
// Expansion permutation
temp = permutation(EP, temp);
// xor temp and round key
temp = xor(temp, key);
// lookup in s-box table
temp = sBox(temp);
// Straight D-box
temp = permutation(P, temp);
// xor
left = xor(left, temp);
System.out.println("Round "
+ (num + 1) + " "
+ right.toUpperCase()
+ " " + left.toUpperCase() + " "
+ key.toUpperCase());
// swapper
return right + left;
}
String encrypt(String plainText, String key)
{
int i;
// get round keys
String keys[] = getKeys(key);
// initial permutation
plainText = permutation(IP, plainText);
System.out.println(
"After initial permutation: "
+ plainText.toUpperCase());
System.out.println(
"After splitting: L0="
+ plainText.substring(0, 8).toUpperCase()
+ " R0="
+ plainText.substring(8, 16).toUpperCase() + "\n");
// 16 rounds
for (i = 0; i < 16; i++) {
plainText = round(plainText, keys[i], i);
}
// 32-bit swap
plainText = plainText.substring(8, 16)
+ plainText.substring(0, 8);
// final permutation
plainText = permutation(IP1, plainText);
return plainText;
}
String decrypt(String plainText, String key)
{
int i;
// get round keys
String keys[] = getKeys(key);
// initial permutation
plainText = permutation(IP, plainText);
System.out.println(
"After initial permutation: "
+ plainText.toUpperCase());
System.out.println(
"After splitting: L0="
+ plainText.substring(0, 8).toUpperCase()
+ " R0=" + plainText.substring(8, 16).toUpperCase()
+ "\n");
// 16-rounds
for (i = 15; i > -1; i--) {
plainText = round(plainText, keys[i], 15 - i);
}
// 32-bit swap
plainText = plainText.substring(8, 16)
+ plainText.substring(0, 8);
plainText = permutation(IP1, plainText);
return plainText;
}
}
public static void main(String args[])
{
String text = "123456ABCD132536";
String key = "AABB09182736CCDD";
DES cipher = new DES();
System.out.println("Encryption:\n");
text = cipher.encrypt(text, key);
System.out.println(
"\nCipher Text: " + text.toUpperCase() + "\n");
System.out.println("Decryption\n");
text = cipher.decrypt(text, key);
System.out.println(
"\nPlain Text: "
+ text.toUpperCase());
}
}
// code contributed by Abhay Bhat
Python
# Hexadecimal to binary conversion
def hex2bin(s):
mp = {'0' : "0000",
'1' : "0001",
'2' : "0010",
'3' : "0011",
'4' : "0100",
'5' : "0101",
'6' : "0110",
'7' : "0111",
'8' : "1000",
'9' : "1001",
'A' : "1010",
'B' : "1011",
'C' : "1100",
'D' : "1101",
'E' : "1110",
'F' : "1111" }
bin = ""
for i in range(len(s)):
bin = bin + mp[s[i]]
return bin
# Binary to hexadecimal conversion
def bin2hex(s):
mp = {"0000" : '0',
"0001" : '1',
"0010" : '2',
"0011" : '3',
"0100" : '4',
"0101" : '5',
"0110" : '6',
"0111" : '7',
"1000" : '8',
"1001" : '9',
"1010" : 'A',
"1011" : 'B',
"1100" : 'C',
"1101" : 'D',
"1110" : 'E',
"1111" : 'F' }
hex = ""
for i in range(0,len(s),4):
ch = ""
ch = ch + s[i]
ch = ch + s[i + 1]
ch = ch + s[i + 2]
ch = ch + s[i + 3]
hex = hex + mp[ch]
return hex
# Binary to decimal conversion
def bin2dec(binary):
binary1 = binary
decimal, i, n = 0, 0, 0
while(binary != 0):
dec = binary % 10
decimal = decimal + dec * pow(2, i)
binary = binary//10
i += 1
return decimal
# Decimal to binary conversion
def dec2bin(num):
res = bin(num).replace("0b", "")
if(len(res)%4 != 0):
div = len(res) / 4
div = int(div)
counter =(4 * (div + 1)) - len(res)
for i in range(0, counter):
res = '0' + res
return res
# Permute function to rearrange the bits
def permute(k, arr, n):
permutation = ""
for i in range(0, n):
permutation = permutation + k[arr[i] - 1]
return permutation
# shifting the bits towards left by nth shifts
def shift_left(k, nth_shifts):
s = ""
for i in range(nth_shifts):
for j in range(1,len(k)):
s = s + k[j]
s = s + k[0]
k = s
s = ""
return k
# calculating xow of two strings of binary number a and b
def xor(a, b):
ans = ""
for i in range(len(a)):
if a[i] == b[i]:
ans = ans + "0"
else:
ans = ans + "1"
return ans
# Table of Position of 64 bits at initial level: Initial Permutation Table
initial_perm = [58, 50, 42, 34, 26, 18, 10, 2,
60, 52, 44, 36, 28, 20, 12, 4,
62, 54, 46, 38, 30, 22, 14, 6,
64, 56, 48, 40, 32, 24, 16, 8,
57, 49, 41, 33, 25, 17, 9, 1,
59, 51, 43, 35, 27, 19, 11, 3,
61, 53, 45, 37, 29, 21, 13, 5,
63, 55, 47, 39, 31, 23, 15, 7]
# Expansion D-box Table
exp_d = [32, 1 , 2 , 3 , 4 , 5 , 4 , 5,
6 , 7 , 8 , 9 , 8 , 9 , 10, 11,
12, 13, 12, 13, 14, 15, 16, 17,
16, 17, 18, 19, 20, 21, 20, 21,
22, 23, 24, 25, 24, 25, 26, 27,
28, 29, 28, 29, 30, 31, 32, 1 ]
# Straight Permutation Table
per = [ 16, 7, 20, 21,
29, 12, 28, 17,
1, 15, 23, 26,
5, 18, 31, 10,
2, 8, 24, 14,
32, 27, 3, 9,
19, 13, 30, 6,
22, 11, 4, 25 ]
# S-box Table
sbox = [[[14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7],
[ 0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8],
[ 4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0],
[15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13 ]],
[[15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10],
[3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5],
[0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15],
[13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9 ]],
[ [10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8],
[13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1],
[13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7],
[1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12 ]],
[ [7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15],
[13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9],
[10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4],
[3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14] ],
[ [2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9],
[14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6],
[4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14],
[11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3 ]],
[ [12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11],
[10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8],
[9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6],
[4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13] ],
[ [4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1],
[13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6],
[1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2],
[6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12] ],
[ [13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7],
[1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2],
[7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8],
[2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11] ] ]
# Final Permutation Table
final_perm = [ 40, 8, 48, 16, 56, 24, 64, 32,
39, 7, 47, 15, 55, 23, 63, 31,
38, 6, 46, 14, 54, 22, 62, 30,
37, 5, 45, 13, 53, 21, 61, 29,
36, 4, 44, 12, 52, 20, 60, 28,
35, 3, 43, 11, 51, 19, 59, 27,
34, 2, 42, 10, 50, 18, 58, 26,
33, 1, 41, 9, 49, 17, 57, 25 ]
def encrypt(pt, rkb, rk):
pt = hex2bin(pt)
# Initial Permutation
pt = permute(pt, initial_perm, 64)
print("After initial permutation", bin2hex(pt))
# Splitting
left = pt[0:32]
right = pt[32:64]
for i in range(0, 16):
# Expansion D-box: Expanding the 32 bits data into 48 bits
right_expanded = permute(right, exp_d, 48)
# XOR RoundKey[i] and right_expanded
xor_x = xor(right_expanded, rkb[i])
# S-boxex: substituting the value from s-box table by calculating row and column
sbox_str = ""
for j in range(0, 8):
row = bin2dec(int(xor_x[j * 6] + xor_x[j * 6 + 5]))
col = bin2dec(int(xor_x[j * 6 + 1] + xor_x[j * 6 + 2] + xor_x[j * 6 + 3] + xor_x[j * 6 + 4]))
val = sbox[j][row][col]
sbox_str = sbox_str + dec2bin(val)
# Straight D-box: After substituting rearranging the bits
sbox_str = permute(sbox_str, per, 32)
# XOR left and sbox_str
result = xor(left, sbox_str)
left = result
# Swapper
if(i != 15):
left, right = right, left
print("Round ", i + 1, " ", bin2hex(left), " ", bin2hex(right), " ", rk[i])
# Combination
combine = left + right
# Final permutation: final rearranging of bits to get cipher text
cipher_text = permute(combine, final_perm, 64)
return cipher_text
pt = "123456ABCD132536"
key = "AABB09182736CCDD"
# Key generation
# --hex to binary
key = hex2bin(key)
# --parity bit drop table
keyp = [57, 49, 41, 33, 25, 17, 9,
1, 58, 50, 42, 34, 26, 18,
10, 2, 59, 51, 43, 35, 27,
19, 11, 3, 60, 52, 44, 36,
63, 55, 47, 39, 31, 23, 15,
7, 62, 54, 46, 38, 30, 22,
14, 6, 61, 53, 45, 37, 29,
21, 13, 5, 28, 20, 12, 4 ]
# getting 56 bit key from 64 bit using the parity bits
key = permute(key, keyp, 56)
# Number of bit shifts
shift_table = [1, 1, 2, 2,
2, 2, 2, 2,
1, 2, 2, 2,
2, 2, 2, 1 ]
# Key- Compression Table : Compression of key from 56 bits to 48 bits
key_comp = [14, 17, 11, 24, 1, 5,
3, 28, 15, 6, 21, 10,
23, 19, 12, 4, 26, 8,
16, 7, 27, 20, 13, 2,
41, 52, 31, 37, 47, 55,
30, 40, 51, 45, 33, 48,
44, 49, 39, 56, 34, 53,
46, 42, 50, 36, 29, 32 ]
# Splitting
left = key[0:28] # rkb for RoundKeys in binary
right = key[28:56] # rk for RoundKeys in hexadecimal
rkb = []
rk = []
for i in range(0, 16):
# Shifting the bits by nth shifts by checking from shift table
left = shift_left(left, shift_table[i])
right = shift_left(right, shift_table[i])
# Combination of left and right string
combine_str = left + right
# Compression of key from 56 to 48 bits
round_key = permute(combine_str, key_comp, 48)
rkb.append(round_key)
rk.append(bin2hex(round_key))
print("Encryption")
cipher_text = bin2hex(encrypt(pt, rkb, rk))
print("Cipher Text : ",cipher_text)
print("Decryption")
rkb_rev = rkb[::-1]
rk_rev = rk[::-1]
text = bin2hex(encrypt(cipher_text, rkb_rev, rk_rev))
print("Plain Text : ",text)
# This code is contributed by Aditya Jain
Producción:
Encryption: After initial permutation: 14A7D67818CA18AD After splitting: L0=14A7D678 R0=18CA18AD Round 1 18CA18AD 5A78E394 194CD072DE8C Round 2 5A78E394 4A1210F6 4568581ABCCE Round 3 4A1210F6 B8089591 06EDA4ACF5B5 Round 4 B8089591 236779C2 DA2D032B6EE3 Round 5 236779C2 A15A4B87 69A629FEC913 Round 6 A15A4B87 2E8F9C65 C1948E87475E Round 7 2E8F9C65 A9FC20A3 708AD2DDB3C0 Round 8 A9FC20A3 308BEE97 34F822F0C66D Round 9 308BEE97 10AF9D37 84BB4473DCCC Round 10 10AF9D37 6CA6CB20 02765708B5BF Round 11 6CA6CB20 FF3C485F 6D5560AF7CA5 Round 12 FF3C485F 22A5963B C2C1E96A4BF3 Round 13 22A5963B 387CCDAA 99C31397C91F Round 14 387CCDAA BD2DD2AB 251B8BC717D0 Round 15 BD2DD2AB CF26B472 3330C5D9A36D Round 16 19BA9212 CF26B472 181C5D75C66D Cipher Text: C0B7A8D05F3A829C Decryption After initial permutation: 19BA9212CF26B472 After splitting: L0=19BA9212 R0=CF26B472 Round 1 CF26B472 BD2DD2AB 181C5D75C66D Round 2 BD2DD2AB 387CCDAA 3330C5D9A36D Round 3 387CCDAA 22A5963B 251B8BC717D0 Round 4 22A5963B FF3C485F 99C31397C91F Round 5 FF3C485F 6CA6CB20 C2C1E96A4BF3 Round 6 6CA6CB20 10AF9D37 6D5560AF7CA5 Round 7 10AF9D37 308BEE97 02765708B5BF Round 8 308BEE97 A9FC20A3 84BB4473DCCC Round 9 A9FC20A3 2E8F9C65 34F822F0C66D Round 10 2E8F9C65 A15A4B87 708AD2DDB3C0 Round 11 A15A4B87 236779C2 C1948E87475E Round 12 236779C2 B8089591 69A629FEC913 Round 13 B8089591 4A1210F6 DA2D032B6EE3 Round 14 4A1210F6 5A78E394 06EDA4ACF5B5 Round 15 5A78E394 18CA18AD 4568581ABCCE Round 16 14A7D678 18CA18AD 194CD072DE8C Plain Text: 123456ABCD132536
Consulte: Diferencia entre los cifrados AES y DES
Publicación traducida automáticamente
Artículo escrito por shubhamupadhyay y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA