Las redes neuronales son el núcleo del aprendizaje profundo, un campo que tiene aplicaciones prácticas en muchas áreas diferentes. Hoy en día, las redes neuronales se utilizan para la clasificación de imágenes, el reconocimiento de voz, la detección de objetos, etc. Ahora, intentemos comprender la unidad básica detrás de todas estas técnicas de vanguardia.
Una sola neurona transforma una entrada dada en alguna salida. Dependiendo de la entrada dada y los pesos asignados a cada entrada, decida si la neurona se disparó o no. Supongamos que la neurona tiene 3 conexiones de entrada y una de salida.
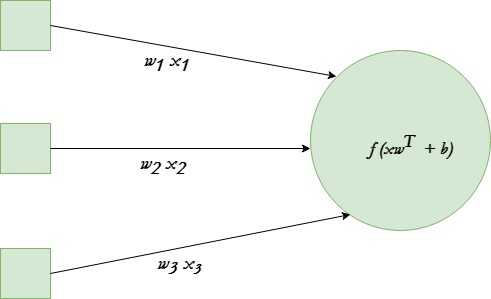
Usaremos la función de activación de tanh en un ejemplo dado.
El objetivo final es encontrar el conjunto óptimo de pesos para esta neurona que produzca resultados correctos. Haz esto entrenando la neurona con varios ejemplos de entrenamiento diferentes. En cada paso, calcule el error en la salida de la neurona y retropropague los gradientes. El paso de calcular la salida de una neurona se denomina propagación hacia adelante, mientras que el cálculo de los gradientes se denomina propagación hacia atrás .
A continuación se muestra la implementación:
Python3
# Python program to implement a
# single neuron neural network
# import all necessary libraries
from numpy import exp, array, random, dot, tanh
# Class to create a neural
# network with single neuron
class NeuralNetwork():
def __init__(self):
# Using seed to make sure it'll
# generate same weights in every run
random.seed(1)
# 3x1 Weight matrix
self.weight_matrix = 2 * random.random((3, 1)) - 1
# tanh as activation function
def tanh(self, x):
return tanh(x)
# derivative of tanh function.
# Needed to calculate the gradients.
def tanh_derivative(self, x):
return 1.0 - tanh(x) ** 2
# forward propagation
def forward_propagation(self, inputs):
return self.tanh(dot(inputs, self.weight_matrix))
# training the neural network.
def train(self, train_inputs, train_outputs,
num_train_iterations):
# Number of iterations we want to
# perform for this set of input.
for iteration in range(num_train_iterations):
output = self.forward_propagation(train_inputs)
# Calculate the error in the output.
error = train_outputs - output
# multiply the error by input and then
# by gradient of tanh function to calculate
# the adjustment needs to be made in weights
adjustment = dot(train_inputs.T, error *
self.tanh_derivative(output))
# Adjust the weight matrix
self.weight_matrix += adjustment
# Driver Code
if __name__ == "__main__":
neural_network = NeuralNetwork()
print ('Random weights at the start of training')
print (neural_network.weight_matrix)
train_inputs = array([[0, 0, 1], [1, 1, 1], [1, 0, 1], [0, 1, 1]])
train_outputs = array([[0, 1, 1, 0]]).T
neural_network.train(train_inputs, train_outputs, 10000)
print ('New weights after training')
print (neural_network.weight_matrix)
# Test the neural network with a new situation.
print ("Testing network on new examples ->")
print (neural_network.forward_propagation(array([1, 0, 0])))
Producción :
Random weights at the start of training [[-0.16595599] [ 0.44064899] [-0.99977125]] New weights after training [[5.39428067] [0.19482422] [0.34317086]] Testing network on new examples -> [0.99995873]
Publicación traducida automáticamente
Artículo escrito por Ravindra_P y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA