Problema de Cobertura Exacta y Algoritmo X | Set 2 (Implementación con DLX)

Posted on by Rudeus Greyrat

En el artículo Problema de Cobertura Exacta y Algoritmo X | En el Conjunto 1 discutimos el problema de Cobertura Exacta y el Algoritmo X para resolver el problema de Cobertura Exacta. En este artículo, discutiremos los detalles de implementación del Algoritmo X usando la Técnica de Enlaces Danzantes (DLX) propuesta por el Dr. Donald E. Knuth en su artículo » Enlaces Danzantes «.

Técnica de enlace de baile

La técnica de enlace de baile se basa en la idea de una lista enlazada doblemente circular . Como se discutió en el artículo anterior , transformamos el problema de la cobertura exacta en forma de array de 0 y 1. Aquí, cada «1» en la array está representado por un Node de lista enlazada y toda la array se transforma en una malla de 4 Nodes conectados. . Cada Node contiene los siguientes campos:

  • Puntero al Node que le queda
  • Puntero al Node derecho a él
  • Puntero al Node por encima de él
  • Puntero al Node debajo de él
  • Puntero para enumerar el Node de encabezado al que pertenece

Cada fila de la array es, por lo tanto, una lista enlazada circular vinculada entre sí con punteros izquierdo y derecho y cada columna de la array también será una lista enlazada circular vinculada a cada una de las anteriores con puntero arriba y abajo. Cada lista de columnas también incluye un Node especial llamado «Node de encabezado de lista». Este Node de encabezado es como un Node simple pero tiene pocos campos adicionales:

  • identificación de la columna
  • Recuento de Nodes en la columna actual

Podemos tener dos tipos diferentes de Nodes, pero en nuestra implementación, crearemos solo un tipo de Node con todos los campos para mayor comodidad con un campo adicional de «ID de fila» que indicará a qué fila pertenece este Node.
Entonces, para la array:
Matrix
la array vinculada de 4 vías se verá así:

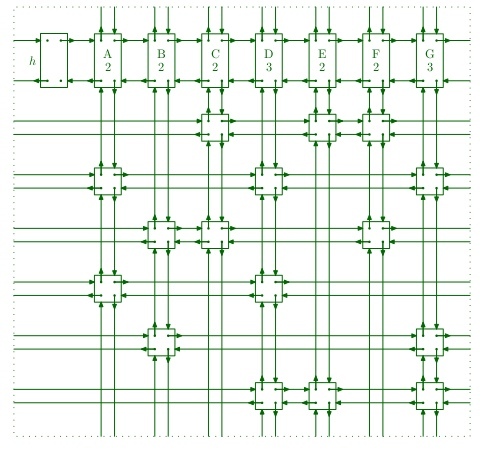
Four way linked matrix

Array ligada de cuatro vías

Entonces, el pseudocódigo para el algoritmo de búsqueda (Algoritmo X) será:

f( h.right == h ) { 
     printSolutions(); 
     return; 
} 
else { 
     ColumnNode column = getMinColumn(); 
     cover(column); 

     for( Node row = column.down ; rowNode != column ;
        rowNode = rowNode.down ) { 
            solutions.add( rowNode ); 

            for( Node rightNode = row.right ; rightNode != row ;
                 rightNode = rightNode.right ) 
                    cover( rightNode ); 

     Search( k+1); 
     solutions.remove( rowNode ); 
     column = rowNode.column; 

     for( Node leftNode = rowNode.left ; leftNode != row ;
              leftNode = leftNode.left )                                                                             
            uncover( leftNode ); 
     } 
     uncover( column ); 
}

Node de cobertura

Como se discutió en el algoritmo, tenemos que eliminar columnas y todas las filas a las que pertenecen los Nodes de esa columna. Este proceso se denomina aquí cobertura del Node.
Para eliminar una columna, simplemente podemos desvincular el encabezado de esa columna de los encabezados vecinos. De esta forma no se puede acceder a esta columna. Este proceso es similar a la eliminación del Node de la lista doblemente enlazada, supongamos que queremos eliminar el Node x entonces:

x.left.right = x.right
x.right.left = x.left

De manera similar, para eliminar una fila, debemos desvincular todos los Nodes de la fila de los Nodes de la fila superior e inferior.

x.up.down = x.down
x.down.up = x.up

Por lo tanto, el pseudocódigo para la cubierta (Node) se convierte en:

Node column = dataNode.column; 

column.right.left = column.left; 
column.left.right = column.right; 

for( Node row = column.down ; row != column ; row = row.down ) 
    for( Node rightNode = row.right ; rightNode != row ; 
         rightNode = rightNode.right ) { 
         rightNode.up.down = rightNode.down; 
         rightNode.down.up = rightNode.up; 
    } 
}

Entonces, por ejemplo, después de cubrir la columna A, la array se verá así:

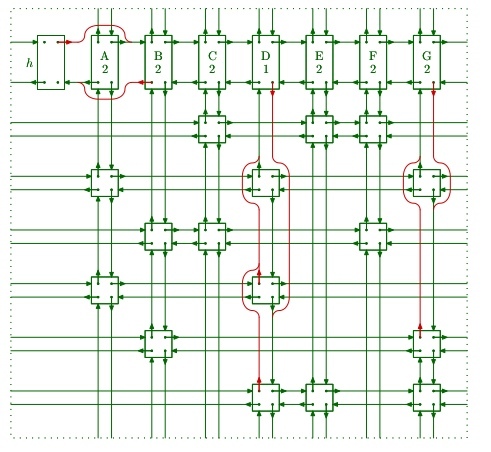
covering

cubierta

Aquí primero eliminamos la columna de otras columnas, luego nos movemos hacia abajo a cada Node de columna y eliminamos la fila atravesando a la derecha, por lo que se eliminan las filas 2 y 4.

Descubrimiento de Node

Supongamos que el algoritmo llegó a un callejón sin salida y no es posible una solución en ese caso, el algoritmo tiene que retroceder. Debido a que hemos eliminado columnas y filas cuando retrocedemos, hemos vuelto a vincular esas filas y columnas eliminadas. Esto es lo que llamamos destape. Tenga en cuenta que los Nodes eliminados aún tienen punteros a sus vecinos, por lo que podemos vincularlos nuevamente usando estos punteros.
Para descubrir la columna, realizaremos la operación de cobertura pero en orden inverso:

x.left.right = x
x.right.left = x

De manera similar, para descubrir cualquier Node de fila x –

x.up.down = x
x.down.up = x

Por lo tanto, el pseudocódigo para descubrir (Node) se convertirá en:

Node column = dataNode.column; 

for( Node row = column.up ; row != column ; row = row.up ) 
    for( Node leftNode = row.left ; leftNode != row ;
         leftNode = leftNode.right ) { 
         leftNode.up.down = leftNode; 
         leftNode.down.up = leftNode; 
     } 
column.right.left = column; 
column.left.right = column; 
}

A continuación se muestra la implementación de la técnica de enlace de baile:

// C++ program for solving exact cover problem
// using DLX (Dancing Links) technique
  
#include <bits/stdc++.h>
  
#define MAX_ROW 100
#define MAX_COL 100
  
using namespace std;
  
struct Node
{
public:
    struct Node *left;
    struct Node *right;
    struct Node *up;
    struct Node *down;
    struct Node *column;
    int rowID;
    int colID;
    int nodeCount;
};
  
// Header node, contains pointer to the
// list header node of first column
struct Node *header = new Node();
  
// Matrix to contain nodes of linked mesh
struct Node Matrix[MAX_ROW][MAX_COL];
  
// Problem Matrix
bool ProbMat[MAX_ROW][MAX_COL];
  
// vector containing solutions
vector <struct Node*> solutions;
  
// Number of rows and columns in problem matrix 
int nRow = 0,nCol = 0;
  
  
// Functions to get next index in any direction
// for given index (circular in nature) 
int getRight(int i){return (i+1) % nCol; }
int getLeft(int i){return (i-1 < 0) ? nCol-1 : i-1 ; }
int getUp(int i){return (i-1 < 0) ? nRow : i-1 ; }  
int getDown(int i){return (i+1) % (nRow+1); }
  
// Create 4 way linked matrix of nodes
// called Toroidal due to resemblance to
// toroid
Node *createToridolMatrix()
{
    // One extra row for list header nodes
    // for each column
    for(int i = 0; i <= nRow; i++)
    {
        for(int j = 0; j < nCol; j++)
        {
            // If it's 1 in the problem matrix then 
            // only create a node 
            if(ProbMat[i][j])
            {
                int a, b;
  
                // If it's 1, other than 1 in 0th row
                // then count it as node of column 
                // and increment node count in column header
                if(i) Matrix[0][j].nodeCount += 1;
  
                // Add pointer to column header for this 
                // column node
                Matrix[i][j].column = &Matrix[0][j];
  
                // set row and column id of this node
                Matrix[i][j].rowID = i;
                Matrix[i][j].colID = j;
  
                // Link the node with neighbors
  
                // Left pointer
                a = i; b = j;
                do{ b = getLeft(b); } while(!ProbMat[a][b] && b != j);
                Matrix[i][j].left = &Matrix[i][b];
  
                // Right pointer
                a = i; b = j;
                do { b = getRight(b); } while(!ProbMat[a][b] && b != j);
                Matrix[i][j].right = &Matrix[i][b];
  
                // Up pointer
                a = i; b = j;
                do { a = getUp(a); } while(!ProbMat[a][b] && a != i);
                Matrix[i][j].up = &Matrix[a][j];
  
                // Down pointer
                a = i; b = j;
                do { a = getDown(a); } while(!ProbMat[a][b] && a != i);
                Matrix[i][j].down = &Matrix[a][j];
            }
        }
    }
  
    // link header right pointer to column 
    // header of first column 
    header->right = &Matrix[0][0];
  
    // link header left pointer to column 
    // header of last column 
    header->left = &Matrix[0][nCol-1];
  
    Matrix[0][0].left = header;
    Matrix[0][nCol-1].right = header;
    return header;
}
  
// Cover the given node completely
void cover(struct Node *targetNode)
{
    struct Node *row, *rightNode;
  
    // get the pointer to the header of column
    // to which this node belong 
    struct Node *colNode = targetNode->column;
  
    // unlink column header from it's neighbors
    colNode->left->right = colNode->right;
    colNode->right->left = colNode->left;
  
    // Move down the column and remove each row
    // by traversing right
    for(row = colNode->down; row != colNode; row = row->down)
    {
        for(rightNode = row->right; rightNode != row;
            rightNode = rightNode->right)
        {
            rightNode->up->down = rightNode->down;
            rightNode->down->up = rightNode->up;
  
            // after unlinking row node, decrement the
            // node count in column header
            Matrix[0][rightNode->colID].nodeCount -= 1;
        }
    }
}
  
// Uncover the given node completely
void uncover(struct Node *targetNode)
{
    struct Node *rowNode, *leftNode;
  
    // get the pointer to the header of column
    // to which this node belong 
    struct Node *colNode = targetNode->column;
  
    // Move down the column and link back
    // each row by traversing left
    for(rowNode = colNode->up; rowNode != colNode; rowNode = rowNode->up)
    {
        for(leftNode = rowNode->left; leftNode != rowNode;
            leftNode = leftNode->left)
        {
            leftNode->up->down = leftNode;
            leftNode->down->up = leftNode;
  
            // after linking row node, increment the
            // node count in column header
            Matrix[0][leftNode->colID].nodeCount += 1;
        }
    }
  
    // link the column header from it's neighbors
    colNode->left->right = colNode;
    colNode->right->left = colNode;
}
  
// Traverse column headers right and 
// return the column having minimum 
// node count
Node *getMinColumn()
{
    struct Node *h = header;
    struct Node *min_col = h->right;
    h = h->right->right;
    do
    {
        if(h->nodeCount < min_col->nodeCount)
        {
            min_col = h;
        }
        h = h->right;
    }while(h != header);
  
    return min_col;
}
  
  
void printSolutions()
{
    cout<<"Printing Solutions: ";
    vector<struct Node*>::iterator i;
  
    for(i = solutions.begin(); i!=solutions.end(); i++)
        cout<<(*i)->rowID<<" ";
    cout<<"\n";
}
  
// Search for exact covers
void search(int k)
{
    struct Node *rowNode;
    struct Node *rightNode;
    struct Node *leftNode;
    struct Node *column;
  
    // if no column left, then we must
    // have found the solution
    if(header->right == header)
    {
        printSolutions();
        return;
    }
  
    // choose column deterministically
    column = getMinColumn();
  
    // cover chosen column
    cover(column);
  
    for(rowNode = column->down; rowNode != column; 
        rowNode = rowNode->down )
    {
        solutions.push_back(rowNode);
  
        for(rightNode = rowNode->right; rightNode != rowNode;
            rightNode = rightNode->right)
            cover(rightNode);
  
        // move to level k+1 (recursively)
        search(k+1);
  
        // if solution in not possible, backtrack (uncover)
        // and remove the selected row (set) from solution
        solutions.pop_back();
  
        column = rowNode->column;
        for(leftNode = rowNode->left; leftNode != rowNode;
            leftNode = leftNode->left)
            uncover(leftNode);
    }
  
    uncover(column);
}
  
// Driver code
int main()
{    
    /*
     Example problem
  
     X = {1,2,3,4,5,6,7}
     set-1 = {1,4,7}
     set-2 = {1,4}
     set-3 = {4,5,7}
     set-4 = {3,5,6}
     set-5 = {2,3,6,7}
     set-6 = {2,7}
     set-7 = {1,4}
  
     Solutions : {6 ,4, 2} and {6, 4, 7}
    */
  
    nRow = 7;
    nCol = 7;
      
    // initialize the problem matrix 
    // ( matrix of 0 and 1) with 0
    for(int i=0; i<=nRow; i++)
    {
        for(int j=0; j<nCol; j++)
        {
            // if it's row 0, it consist of column
            // headers. Initialize it with 1
            if(i == 0) ProbMat[i][j] = true;
            else ProbMat[i][j] = false;
        }
    }
  
    // Manually filling up 1's 
    ProbMat[1][0] = true; ProbMat[1][3] = true;
    ProbMat[1][6] = true; ProbMat[2][0] = true;
    ProbMat[2][3] = true; ProbMat[3][3] = true;
    ProbMat[3][4] = true; ProbMat[3][6] = true;
    ProbMat[4][2] = true; ProbMat[4][4] = true;
    ProbMat[4][5] = true; ProbMat[5][1] = true;
    ProbMat[5][2] = true; ProbMat[5][5] = true;
    ProbMat[5][6] = true; ProbMat[6][1] = true;
    ProbMat[6][6] = true; ProbMat[7][0] = true;
    ProbMat[7][3] = true;
  
    // create 4-way linked matrix
    createToridolMatrix();
      
    search(0);
    return 0;
}

Producción:

Printing Solutions: 6 4 2 
Printing Solutions: 6 4 7

Referencias

Este artículo es una contribución de Atul Kumar . Si le gusta GeeksforGeeks y le gustaría contribuir, también puede escribir un artículo usando contribuya.geeksforgeeks.org o envíe su artículo por correo a contribuya@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.

Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.

Publicación traducida automáticamente

Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *