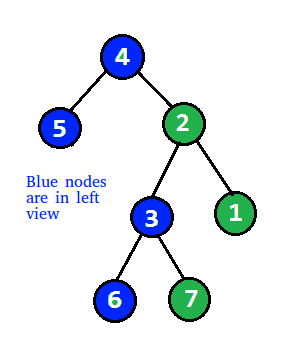
Dado un árbol binario, imprima la vista izquierda del mismo. La vista izquierda de un árbol binario es un conjunto de Nodes visibles cuando se visita el árbol desde el lado izquierdo.
C++
// C++ program to print left view of Binary Tree
#include <bits/stdc++.h>
using namespace std;
struct Node
{
int data;
struct Node *left, *right;
};
// A utility function to
// create a new Binary Tree Node
struct Node *newNode(int item)
{
struct Node *temp = (struct Node *)malloc(
sizeof(struct Node));
temp->data = item;
temp->left = temp->right = NULL;
return temp;
}
// Recursive function to print
// left view of a binary tree.
void leftViewUtil(struct Node *root,
int level, int *max_level)
{
// Base Case
if (root == NULL) return;
// If this is the first Node of its level
if (*max_level < level)
{
cout << root->data << " ";
*max_level = level;
}
// Recur for left subtree first,
// then right subtree
leftViewUtil(root->left, level + 1, max_level);
leftViewUtil(root->right, level + 1, max_level);
}
// A wrapper over leftViewUtil()
void leftView(struct Node *root)
{
int max_level = 0;
leftViewUtil(root, 1, &max_level);
}
// Driver Code
int main()
{
Node* root = newNode(10);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(7);
root->left->right = newNode(8);
root->right->right = newNode(15);
root->right->left = newNode(12);
root->right->right->left = newNode(14);
leftView(root);
return 0;
}
C
// C program to print left view of Binary Tree
#include <stdio.h>
#include <stdlib.h>
struct node {
int data;
struct node *left, *right;
};
// A utility function to create a new Binary Tree node
struct node* newNode(int item)
{
struct node* temp
= (struct node*)malloc(sizeof(struct node));
temp->data = item;
temp->left = temp->right = NULL;
return temp;
}
// Recursive function to print left view of a binary tree.
void leftViewUtil(struct node* root, int level,
int* max_level)
{
// Base Case
if (root == NULL)
return;
// If this is the first node of its level
if (*max_level < level) {
printf("%d\t", root->data);
*max_level = level;
}
// Recur for left and right subtrees
leftViewUtil(root->left, level + 1, max_level);
leftViewUtil(root->right, level + 1, max_level);
}
// A wrapper over leftViewUtil()
void leftView(struct node* root)
{
int max_level = 0;
leftViewUtil(root, 1, &max_level);
}
// Driver code
int main()
{
struct node* root = newNode(10);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(7);
root->left->right = newNode(8);
root->right->right = newNode(15);
root->right->left = newNode(12);
root->right->right->left = newNode(14);
leftView(root);
return 0;
}
Java
// Java program to print left view of binary tree
/* Class containing left and right child of current
node and key value*/
class Node {
int data;
Node left, right;
public Node(int item)
{
data = item;
left = right = null;
}
}
/* Class to print the left view */
class BinaryTree {
Node root;
static int max_level = 0;
// recursive function to print left view
void leftViewUtil(Node node, int level)
{
// Base Case
if (node == null)
return;
// If this is the first node of its level
if (max_level < level) {
System.out.print(" " + node.data);
max_level = level;
}
// Recur for left and right subtrees
leftViewUtil(node.left, level + 1);
leftViewUtil(node.right, level + 1);
}
// A wrapper over leftViewUtil()
void leftView()
{
max_level = 0;
leftViewUtil(root, 1);
}
/* testing for example nodes */
public static void main(String args[])
{
/* creating a binary tree and entering the nodes */
BinaryTree tree = new BinaryTree();
tree.root = new Node(10);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(7);
tree.root.left.right = new Node(8);
tree.root.right.right = new Node(15);
tree.root.right.left = new Node(12);
tree.root.right.right.left = new Node(14);
tree.leftView();
}
}
Python
# Python program to print left view of Binary Tree # A binary tree node class Node: # Constructor to create a new node def __init__(self, data): self.data = data self.left = None self.right = None # Recursive function print left view of a binary tree def leftViewUtil(root, level, max_level): # Base Case if root is None: return # If this is the first node of its level if (max_level[0] < level): print "% d\t" %(root.data), max_level[0] = level # Recur for left and right subtree leftViewUtil(root.left, level + 1, max_level) leftViewUtil(root.right, level + 1, max_level) # A wrapper over leftViewUtil() def leftView(root): max_level = [0] leftViewUtil(root, 1, max_level) # Driver program to test above function root = Node(10) root.left = Node(2) root.right = Node(3) root.left.left = Node(7) root.left.right = Node(8) root.right.right = Node(15) root.right.left = Node(12) root.right.right.left = Node(14) leftView(root) # This code is contributed by Nikhil Kumar Singh(nickzuck_007)
C#
using System;
// C# program to print left view of binary tree
/* Class containing left and right child of current
node and key value*/
public class Node {
public int data;
public Node left, right;
public Node(int item)
{
data = item;
left = right = null;
}
}
/* Class to print the left view */
public class BinaryTree {
public Node root;
public static int max_level = 0;
// recursive function to print left view
public virtual void leftViewUtil(Node node, int level)
{
// Base Case
if (node == null) {
return;
}
// If this is the first node of its level
if (max_level < level) {
Console.Write(" " + node.data);
max_level = level;
}
// Recur for left and right subtrees
leftViewUtil(node.left, level + 1);
leftViewUtil(node.right, level + 1);
}
// A wrapper over leftViewUtil()
public virtual void leftView()
{
leftViewUtil(root, 1);
}
/* testing for example nodes */
public static void Main(string[] args)
{
/* creating a binary tree and entering the nodes */
BinaryTree tree = new BinaryTree();
tree.root = new Node(10);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(7);
tree.root.left.right = new Node(8);
tree.root.right.right = new Node(15);
tree.root.right.left = new Node(12);
tree.root.right.right.left = new Node(14);
tree.leftView();
}
}
// This code is contributed by Shrikant13
Javascript
<script>
// Javascript program to print left view
// of binary tree
// Class containing left and right
// child of current node and key value
class Node
{
constructor(item)
{
this.data = item;
this.left = null;
this.right = null;
}
}
// Class to print the left view
var root ;
var max_level = 0;
// Recursive function to print left view
function leftViewUtil(node, level)
{
// Base Case
if (node == null)
{
return;
}
// If this is the first node of its level
if (max_level < level)
{
document.write(" " + node.data);
max_level = level;
}
// Recur for left and right subtrees
leftViewUtil(node.left, level + 1);
leftViewUtil(node.right, level + 1);
}
// A wrapper over leftViewUtil()
function leftView()
{
leftViewUtil(root, 1);
}
// Driver code
// Testing for example nodes
// Creating a binary tree and
// entering the nodes
root = Node(10)
root.left = new Node(2)
root.right = new Node(3)
root.left.left = new Node(7)
root.left.right = new Node(8)
root.right.right = new Node(15)
root.right.left = new Node(12)
root.right.right.left = new Node(14)
leftView();
// This code is contributed by rrrtnx
</script>
C++
// C++ program to print left view of
// Binary Tree
#include<bits/stdc++.h>
using namespace std;
// A Binary Tree Node
struct Node
{
int data;
struct Node *left, *right;
};
// Utility function to create a new tree node
Node* newNode(int data)
{
Node *temp = new Node;
temp->data = data;
temp->left = temp->right = NULL;
return temp;
}
// function to print left view of
// binary tree
void printLeftView(Node* root)
{
if (!root)
return;
queue<Node*> q;
q.push(root);
while (!q.empty())
{
// number of nodes at current level
int n = q.size();
// Traverse all nodes of current level
for(int i = 1; i <= n; i++)
{
Node* temp = q.front();
q.pop();
// Print the left most element
// at the level
if (i == 1)
cout<<temp->data<<" ";
// Add left node to queue
if (temp->left != NULL)
q.push(temp->left);
// Add right node to queue
if (temp->right != NULL)
q.push(temp->right);
}
}
}
// Driver code
int main()
{
// Let's construct the tree as
// shown in example
Node* root = newNode(10);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(7);
root->left->right = newNode(8);
root->right->right = newNode(15);
root->right->left = newNode(12);
root->right->right->left = newNode(14);
printLeftView(root);
}
// This code is contributed by
// Manne SreeCharan
Java
// Java program to print left view of Binary
// Tree
import java.util.*;
public class PrintRightView {
// Binary tree node
private static class Node {
int data;
Node left, right;
public Node(int data)
{
this.data = data;
this.left = null;
this.right = null;
}
}
// function to print left view of binary tree
private static void printLeftView(Node root)
{
if (root == null)
return;
Queue<Node> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()) {
// number of nodes at current level
int n = queue.size();
// Traverse all nodes of current level
for (int i = 1; i <= n; i++) {
Node temp = queue.poll();
// Print the left most element at
// the level
if (i == 1)
System.out.print(temp.data + " ");
// Add left node to queue
if (temp.left != null)
queue.add(temp.left);
// Add right node to queue
if (temp.right != null)
queue.add(temp.right);
}
}
}
// Driver code
public static void main(String[] args)
{
// construct binary tree as shown in
// above diagram
Node root = new Node(10);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(7);
root.left.right = new Node(8);
root.right.right = new Node(15);
root.right.left = new Node(12);
root.right.right.left = new Node(14);
printLeftView(root);
}
}
// This code is contributed by
// Manne SreeCharan
Python
# Python3 program to print left view of # Binary Tree # Binary Tree Node """ utility that allocates a newNode with the given key """ class newNode: # Construct to create a newNode def __init__(self, key): self.data = key self.left = None self.right = None self.hd = 0 # function to print left view of # binary tree def printLeftView(root): if (not root): return q = [] q.append(root) while (len(q)): # number of nodes at current level n = len(q) # Traverse all nodes of current level for i in range(1, n + 1): temp = q[0] q.pop(0) # Print the left most element # at the level if (i == 1): print(temp.data, end=" ") # Add left node to queue if (temp.left != None): q.append(temp.left) # Add right node to queue if (temp.right != None): q.append(temp.right) # Driver Code if __name__ == '__main__': root = newNode(10) root.left = newNode(2) root.right = newNode(3) root.left.left = newNode(7) root.left.right = newNode(8) root.right.right = newNode(15) root.right.left = newNode(12) root.right.right.left = newNode(14) printLeftView(root) # This code is contributed by # Manne SreeCharan
C#
// C# program to print left view
// of Binary Tree
using System;
using System.Collections.Generic;
public class PrintRightView {
// Binary tree node
private class Node {
public int data;
public Node left, right;
public Node(int data)
{
this.data = data;
this.left = null;
this.right = null;
}
}
// function to print left view of binary tree
private static void printRightView(Node root)
{
if (root == null)
return;
Queue<Node> queue = new Queue<Node>();
queue.Enqueue(root);
while (queue.Count != 0) {
// number of nodes at current level
int n = queue.Count;
// Traverse all nodes of current level
for (int i = 1; i <= n; i++) {
Node temp = queue.Dequeue();
// Print the left most element at
// the level
if (i == n)
Console.Write(temp.data + " ");
// Add left node to queue
if (temp.left != null)
queue.Enqueue(temp.left);
// Add right node to queue
if (temp.right != null)
queue.Enqueue(temp.right);
}
}
}
// Driver code
public static void Main(String[] args)
{
// construct binary tree as shown in
// above diagram
Node root = new Node(10);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(7);
root.left.right = new Node(8);
root.right.right = new Node(15);
root.right.left = new Node(12);
root.right.right.left = new Node(14);
printRightView(root);
}
}
// This code is contributed Manne SreeCharan
Javascript
<script>
// JavaScript program to print left view of
// Binary Tree
class newNode{
// Construct to create a newNode
constructor(key){
this.data = key
this.left = null
this.right = null
this.hd = 0
}
}
// function to print left view of
// binary tree
function printLeftView(root){
if (root == null)
return
let q = []
q.push(root)
while (q.length){
// number of nodes at current level
let n = q.length
// Traverse all nodes of current level
for(let i=1;i< n + 1;i++){
let temp = q.shift()
// Print the left most element
// at the level
if (i == 1)
document.write(temp.data," ")
// Add left node to queue
if (temp.left != null)
q.push(temp.left)
// Add right node to queue
if (temp.right != null)
q.push(temp.right)
}
}
}
// Driver Code
let root = new newNode(10)
root.left = new newNode(2)
root.right = new newNode(3)
root.left.left = new newNode(7)
root.left.right = new newNode(8)
root.right.right = new newNode(15)
root.right.left = new newNode(12)
root.right.right.left = new newNode(14)
printLeftView(root)
// This code is contributed by shinjanpatra
</script>
C++
#include <bits/stdc++.h>
using namespace std;
struct Node
{
int data;
struct Node *left, *right;
};
// A utility function to
// create a new Binary Tree Node
struct Node *newNode(int item)
{
struct Node *temp = (struct Node *)malloc(
sizeof(struct Node));
temp->data = item;
temp->left = temp->right = NULL;
return temp;
}
vector<int> leftView(Node *root)
{
// Your code here
vector<int>ans;
if(!root)
{
return ans;
}
queue<Node*>q;
q.push(root);
q.push(NULL);
bool ok=true;
while(!q.empty())
{
auto it=q.front();
q.pop();
if(it==NULL)
{
if(ok==false)
{
ok=true;
}
if(q.size()==0)
{
break;
}
else
{
q.push(NULL);
}
}
else
{
if(ok)
{
ans.push_back(it->data);
ok=false;
}
if(it->left)
{
q.push(it->left);
}
if(it->right)
{
q.push(it->right);
}
}
}
return ans;
}
int main()
{
Node* root = newNode(10);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(7);
root->left->right = newNode(8);
root->right->right = newNode(15);
root->right->left = newNode(12);
root->right->right->left = newNode(14);
vector<int> vec = leftView(root);
for(int x : vec)
cout<<x<<" ";
cout << endl;
return 0;
}
Java
// Java Program to print the left view
import java.util.*;
class GFG {
// Binary Tree Node
static class Node {
int data;
Node left, right;
public Node(int item)
{
data = item;
left = right = null;
}
};
// function to print the left view of binary tree
public static ArrayList<Integer> leftView(Node root)
{
// Your code here
ArrayList<Integer> ans = new ArrayList<>();
if (root == null) {
return ans;
}
Queue<Node> q = new LinkedList<>();
q.add(root);
q.add(null);
boolean ok = true;
while (!q.isEmpty()) {
Node it = q.poll();
if (it == null) {
if (ok == false) {
ok = true;
}
if (q.size() == 0)
break;
else {
q.add(null);
}
}
else {
if (ok) {
ans.add(it.data);
ok = false;
}
if (it.left != null) {
q.add(it.left);
}
if (it.right != null) {
q.add(it.right);
}
}
}
return ans;
}
// driver code
public static void main(String[] args)
{
Node root = new Node(10);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(7);
root.left.right = new Node(8);
root.right.right = new Node(15);
root.right.left = new Node(12);
root.right.right.left = new Node(14);
ArrayList<Integer> vec = leftView(root);
for (int x : vec) {
System.out.print(x + " ");
}
System.out.println();
}
}
// This code is contributed by Tapesh(tapeshdua420)
Python3
# Python Program to print left view # Tree Node Class class Node: def __init__(self, data): self.data = data self.left = None self.right = None # function to get the left view of binary tree def leftView(root): ans = [] if not root: return ans q = [] q.append(root) q.append(None) ok = True while len(q) != 0: it = q[0] del q[0] if it == None: if ok == False: ok = True if len(q) == 0: break else: q.append(None) else: if ok: ans.append(it.data) ok = False if it.left != None: q.append(it.left) if it.right != None: q.append(it.right) return ans # Driver Code if __name__ == '__main__': root = Node(10) root.left = Node(2) root.right = Node(3) root.left.left = Node(7) root.left.right = Node(8) root.right.right = Node(15) root.right.left = Node(12) root.right.right.left = Node(14) vec = leftView(root) # print the left view for x in vec: print(x, end=" ") print() # This code is contributed by Tapesh(tapeshdua420)
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA