Un gráfico es una presentación de un conjunto de entidades donde algunos pares de entidades están vinculados por una conexión. Las entidades interconectadas se representan mediante puntos denominados vértices, y las conexiones entre los vértices se denominan aristas. Formalmente, un gráfico es un par de conjuntos (V, E), donde V es una colección de vértices y E es una colección de aristas que unen un par de vértices.
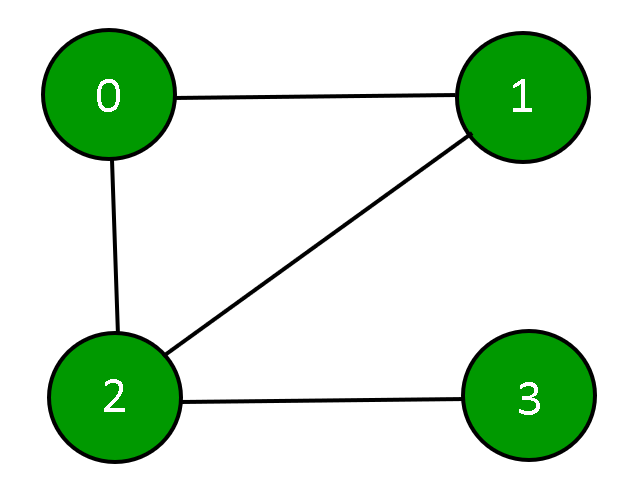
Un gráfico se puede representar usando una Array de Adyacencia.
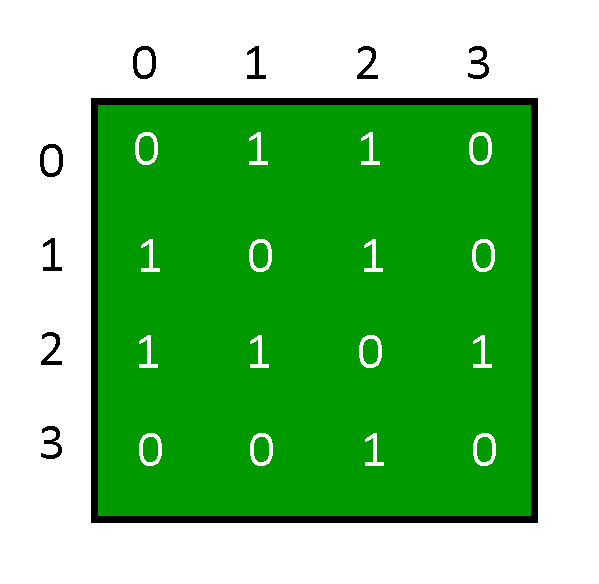
Inicialización del gráfico: la array de adyacencia se representará usando una array 2D, se usará un constructor para asignar el tamaño de la array y cada elemento de esa array se inicializará en 0. Demostrando que el grado de cada vértice en el gráfico es cero.
C++
class Graph {
private:
// number of vertices
int n;
// adjacency matrix
int g[10][10];
public:
// constructor
Graph(int x)
{
n = x;
// initializing each element of the adjacency matrix to zero
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
g[i][j] = 0;
}
}
}
};
Java
class Graph {
// number of vertices
private int n;
// adjacency matrix
private int[][] g = new int[10][10];
// constructor
Graph(int x)
{
this.n = x;
int i, j;
// initializing each element of the adjacency matrix to zero
for (i = 0; i < n; ++i) {
for (j = 0; j < n; ++j) {
g[i][j] = 0;
}
}
}
}
Python3
class Graph: # number of vertices __n = 0 # adjacency matrix __g =[[0 for x in range(10)] for y in range(10)] # constructor def __init__(self, x): self.__n = x # initializing each element of the adjacency matrix to zero for i in range(0, self.__n): for j in range(0, self.__n): self.__g[i][j]= 0
C#
class Graph{
// Number of vertices
private int n;
// Adjacency matrix
private int[,] g = new int[10, 10];
// Constructor
Graph(int x)
{
this.n = x;
int i, j;
// Initializing each element of
// the adjacency matrix to zero
for(i = 0; i < n; ++i)
{
for(j = 0; j < n; ++j)
{
g[i, j] = 0;
}
}
}
}
// This code is contributed by ukasp
Aquí la array de adyacencia es g[n][n] en la que el grado de cada vértice es cero.
Visualización del gráfico: el gráfico se representa utilizando la array de adyacencia g[n][n] que tiene el número de vértices n. Se muestra la array 2D (array de adyacencia) en la que si hay un borde entre dos vértices ‘x’ e ‘y’, entonces g[x][y] es 1; de lo contrario, 0.
C++
void displayAdjacencyMatrix()
{
cout << "\n\n Adjacency Matrix:";
// displaying the 2D array
for (int i = 0; i < n; ++i) {
cout << "\n";
for (int j = 0; j < n; ++j) {
cout << " " << g[i][j];
}
}
}
Java
public void displayAdjacencyMatrix()
{
System.out.print("\n\n Adjacency Matrix:");
// displaying the 2D array
for (int i = 0; i < n; ++i) {
System.out.println();
for (int j = 0; j < n; ++j) {
System.out.print(" " + g[i][j]);
}
}
}
Python3
def displayAdjacencyMatrix(self):
print("\n\n Adjacency Matrix:", end ="")
# displaying the 2D array
for i in range(0, self.__n):
print()
for j in range(0, self.__n):
print("", self.__g[i][j], end ="")
El método anterior es una función miembro pública de la clase Graph que muestra el gráfico usando una array de adyacencia.
Agregar bordes entre vértices en el gráfico: para agregar bordes entre dos vértices existentes, como el vértice ‘x’ y el vértice ‘y’, los elementos g[x][y] y g[y][x] de la array de adyacencia serán asignado a 1, que representa que hay un borde entre el vértice ‘x’ y el vértice ‘y’.
C++
void addEdge(int x, int y)
{
// checks if the vertex exists in the graph
if ((x >= n) || (y > n)) {
cout << "Vertex does not exists!";
}
// checks if the vertex is connecting to itself
if (x == y) {
cout << "Same Vertex!";
}
else {
// connecting the vertices
g[y][x] = 1;
g[x][y] = 1;
}
}
Java
public void addEdge(int x, int y)
{
// checks if the vertex exists in the graph
if ((x >= n) || (y > n)) {
System.out.println("Vertex does not exists!");
}
// checks if the vertex is connecting to itself
if (x == y) {
System.out.println("Same Vertex!");
}
else {
// connecting the vertices
g[y][x] = 1;
g[x][y] = 1;
}
}
Python3
def addEdge(self, x, y):
# checks if the vertex exists in the graph
if(x>= self.__n) or (y >= self.__n):
print("Vertex does not exists !")
# checks if the vertex is connecting to itself
if(x == y):
print("Same Vertex !")
else:
# connecting the vertices
self.__g[y][x]= 1
self.__g[x][y]= 1
Aquí, el método anterior es una función miembro pública de la clase Graph que conecta dos vértices existentes en el gráfico.
Agregar un vértice en el gráfico: para agregar un vértice en el gráfico, necesitamos aumentar tanto la fila como la columna de la array de adyacencia existente y luego inicializar los nuevos elementos relacionados con ese vértice a 0. (es decir, el nuevo vértice agregado no es conectado a cualquier otro vértice)
C++
void addVertex()
{
// increasing the number of vertices
n++;
int i;
// initializing the new elements to 0
for (i = 0; i < n; ++i) {
g[i][n - 1] = 0;
g[n - 1][i] = 0;
}
}
Java
public void addVertex()
{
// increasing the number of vertices
n++;
int i;
// initializing the new elements to 0
for (i = 0; i < n; ++i) {
g[i][n - 1] = 0;
g[n - 1][i] = 0;
}
}
Python3
def addVertex(self): # increasing the number of vertices self.__n = self.__n + 1; # initializing the new elements to 0 for i in range(0, self.__n): self.__g[i][self.__n-1]= 0 self.__g[self.__n-1][i]= 0
El método anterior es una función miembro pública de la clase Graph que incrementa el número de vértices en 1 y el grado del nuevo vértice es 0.
Eliminación de un vértice en el gráfico: para eliminar un vértice del gráfico, debemos verificar si ese vértice existe en el gráfico o no, y si ese vértice existe, debemos desplazar las filas hacia la izquierda y las columnas hacia arriba de la adyacencia. array para que los valores de fila y columna del vértice dado se reemplacen por los valores del siguiente vértice y luego disminuya el número de vértices en 1. De esta manera, ese vértice en particular se eliminará de la array de adyacencia.
C++
void removeVertex(int x)
{
// checking if the vertex is present
if (x > n) {
cout << "\nVertex not present!";
return;
}
else {
int i;
// removing the vertex
while (x < n) {
// shifting the rows to left side
for (i = 0; i < n; ++i) {
g[i][x] = g[i][x + 1];
}
// shifting the columns upwards
for (i = 0; i < n; ++i) {
g[x][i] = g[x + 1][i];
}
x++;
}
// decreasing the number of vertices
n--;
}
}
Java
public void removeVertex(int x)
{
// checking if the vertex is present
if (x > n) {
System.out.println("Vertex not present!");
return;
}
else {
int i;
// removing the vertex
while (x < n) {
// shifting the rows to left side
for (i = 0; i < n; ++i) {
g[i][x] = g[i][x + 1];
}
// shifting the columns upwards
for (i = 0; i < n; ++i) {
g[x][i] = g[x + 1][i];
}
x++;
}
// decreasing the number of vertices
n--;
}
}
Python3
def removeVertex(self, x):
# checking if the vertex is present
if(x>self.__n):
print("Vertex not present !")
else:
# removing the vertex
while(x<self.__n):
# shifting the rows to left side
for i in range(0, self.__n):
self.__g[i][x]= self.__g[i][x + 1]
# shifting the columns upwards
for i in range(0, self.__n):
self.__g[x][i]= self.__g[x + 1][i]
x = x + 1
# decreasing the number of vertices
self.__n = self.__n - 1
El método anterior es una función miembro pública de la clase Graph que elimina un vértice existente del gráfico desplazando las filas hacia la izquierda y desplazando las columnas hacia arriba para reemplazar los valores de fila y columna de ese vértice con el siguiente vértice y luego disminuye el número de vértices por 1 en el gráfico.
El siguiente es un programa completo que utiliza todos los métodos anteriores en un gráfico.
C++
// C++ program to add and remove Vertex in Adjacency Matrix
#include <iostream>
using namespace std;
class Graph {
private:
// number of vertices
int n;
// adjacency matrix
int g[10][10];
public:
// constructor
Graph(int x)
{
n = x;
// initializing each element of the adjacency matrix to zero
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
g[i][j] = 0;
}
}
}
void displayAdjacencyMatrix()
{
cout << "\n\n Adjacency Matrix:";
// displaying the 2D array
for (int i = 0; i < n; ++i) {
cout << "\n";
for (int j = 0; j < n; ++j) {
cout << " " << g[i][j];
}
}
}
void addEdge(int x, int y)
{
// checks if the vertex exists in the graph
if ((x >= n) || (y > n)) {
cout << "Vertex does not exists!";
}
// checks if the vertex is connecting to itself
if (x == y) {
cout << "Same Vertex!";
}
else {
// connecting the vertices
g[y][x] = 1;
g[x][y] = 1;
}
}
void addVertex()
{
// increasing the number of vertices
n++;
int i;
// initializing the new elements to 0
for (i = 0; i < n; ++i) {
g[i][n - 1] = 0;
g[n - 1][i] = 0;
}
}
void removeVertex(int x)
{
// checking if the vertex is present
if (x > n) {
cout << "\nVertex not present!";
return;
}
else {
int i;
// removing the vertex
while (x < n) {
// shifting the rows to left side
for (i = 0; i < n; ++i) {
g[i][x] = g[i][x + 1];
}
// shifting the columns upwards
for (i = 0; i < n; ++i) {
g[x][i] = g[x + 1][i];
}
x++;
}
// decreasing the number of vertices
n--;
}
}
};
int main()
{
// creating objects of class Graph
Graph obj(4);
// calling methods
obj.addEdge(0, 1);
obj.addEdge(0, 2);
obj.addEdge(1, 2);
obj.addEdge(2, 3);
// the adjacency matrix created
obj.displayAdjacencyMatrix();
// adding a vertex to the graph
obj.addVertex();
// connecting that vertex to other existing vertices
obj.addEdge(4, 1);
obj.addEdge(4, 3);
// the adjacency matrix with a new vertex
obj.displayAdjacencyMatrix();
// removing an existing vertex in the graph
obj.removeVertex(1);
// the adjacency matrix after removing a vertex
obj.displayAdjacencyMatrix();
return 0;
}
Java
// Java program to add and remove Vertex in Adjacency Matrix
class Graph
{
// number of vertices
private int n;
// adjacency matrix
private int[][] g = new int[10][10];
// constructor
Graph(int x)
{
this.n = x;
int i, j;
// initializing each element of
// the adjacency matrix to zero
for (i = 0; i < n; ++i)
{
for (j = 0; j < n; ++j)
{
g[i][j] = 0;
}
}
}
public void displayAdjacencyMatrix()
{
System.out.print("\n\n Adjacency Matrix:");
// displaying the 2D array
for (int i = 0; i < n; ++i)
{
System.out.println();
for (int j = 0; j < n; ++j)
{
System.out.print(" " + g[i][j]);
}
}
}
public void addEdge(int x, int y)
{
// checks if the vertex exists in the graph
if ((x >= n) || (y > n))
{
System.out.println("Vertex does not exists!");
}
// checks if the vertex is connecting to itself
if (x == y)
{
System.out.println("Same Vertex!");
}
else
{
// connecting the vertices
g[y][x] = 1;
g[x][y] = 1;
}
}
public void addVertex()
{
// increasing the number of vertices
n++;
int i;
// initializing the new elements to 0
for (i = 0; i < n; ++i)
{
g[i][n - 1] = 0;
g[n - 1][i] = 0;
}
}
public void removeVertex(int x)
{
// checking if the vertex is present
if (x > n)
{
System.out.println("Vertex not present!");
return;
}
else
{
int i;
// removing the vertex
while (x < n)
{
// shifting the rows to left side
for (i = 0; i < n; ++i)
{
g[i][x] = g[i][x + 1];
}
// shifting the columns upwards
for (i = 0; i < n; ++i)
{
g[x][i] = g[x + 1][i];
}
x++;
}
// decreasing the number of vertices
n--;
}
}
}
class Main
{
public static void main(String[] args)
{
// creating objects of class Graph
Graph obj = new Graph(4);
// calling methods
obj.addEdge(0, 1);
obj.addEdge(0, 2);
obj.addEdge(1, 2);
obj.addEdge(2, 3);
// the adjacency matrix created
obj.displayAdjacencyMatrix();
// adding a vertex to the graph
obj.addVertex();
// connecting that vertex to other existing vertices
obj.addEdge(4, 1);
obj.addEdge(4, 3);
// the adjacency matrix with a new vertex
obj.displayAdjacencyMatrix();
// removing an existing vertex in the graph
obj.removeVertex(1);
// the adjacency matrix after removing a vertex
obj.displayAdjacencyMatrix();
}
}
Python3
# Python program to add and remove Vertex in Adjacency Matrix
class Graph:
# number of vertices
__n = 0
# adjacency matrix
__g =[[0 for x in range(10)] for y in range(10)]
# constructor
def __init__(self, x):
self.__n = x
# initializing each element of the adjacency matrix to zero
for i in range(0, self.__n):
for j in range(0, self.__n):
self.__g[i][j]= 0
def displayAdjacencyMatrix(self):
print("\n\n Adjacency Matrix:", end ="")
# displaying the 2D array
for i in range(0, self.__n):
print()
for j in range(0, self.__n):
print("", self.__g[i][j], end ="")
def addEdge(self, x, y):
# checks if the vertex exists in the graph
if(x>= self.__n) or (y >= self.__n):
print("Vertex does not exists !")
# checks if the vertex is connecting to itself
if(x == y):
print("Same Vertex !")
else:
# connecting the vertices
self.__g[y][x]= 1
self.__g[x][y]= 1
def addVertex(self):
# increasing the number of vertices
self.__n = self.__n + 1;
# initializing the new elements to 0
for i in range(0, self.__n):
self.__g[i][self.__n-1]= 0
self.__g[self.__n-1][i]= 0
def removeVertex(self, x):
# checking if the vertex is present
if(x>self.__n):
print("Vertex not present !")
else:
# removing the vertex
while(x<self.__n):
# shifting the rows to left side
for i in range(0, self.__n):
self.__g[i][x]= self.__g[i][x + 1]
# shifting the columns upwards
for i in range(0, self.__n):
self.__g[x][i]= self.__g[x + 1][i]
x = x + 1
# decreasing the number of vertices
self.__n = self.__n - 1
# creating objects of class Graph
obj = Graph(4);
# calling methods
obj.addEdge(0, 1);
obj.addEdge(0, 2);
obj.addEdge(1, 2);
obj.addEdge(2, 3);
# the adjacency matrix created
obj.displayAdjacencyMatrix();
# adding a vertex to the graph
obj.addVertex();
# connecting that vertex to other existing vertices
obj.addEdge(4, 1);
obj.addEdge(4, 3);
# the adjacency matrix with a new vertex
obj.displayAdjacencyMatrix();
# removing an existing vertex in the graph
obj.removeVertex(1);
# the adjacency matrix after removing a vertex
obj.displayAdjacencyMatrix();
C#
// C# program to add and remove Vertex in Adjacency Matrix
using System;
public class Graph
{
// number of vertices
private int n;
// adjacency matrix
private int[,] g = new int[10, 10];
// constructor
public Graph(int x)
{
this.n = x;
int i, j;
// initializing each element of the adjacency matrix to zero
for (i = 0; i < n; ++i)
{
for (j = 0; j < n; ++j)
{
g[i, j] = 0;
}
}
}
public void displayAdjacencyMatrix()
{
Console.Write("\n\n Adjacency Matrix:");
// displaying the 2D array
for (int i = 0; i < n; ++i)
{
Console.WriteLine();
for (int j = 0; j < n; ++j)
{
Console.Write(" " + g[i, j]);
}
}
}
public void addEdge(int x, int y)
{
// checks if the vertex exists in the graph
if ((x >= n) || (y > n))
{
Console.WriteLine("Vertex does not exists!");
}
// checks if the vertex is connecting to itself
if (x == y)
{
Console.WriteLine("Same Vertex!");
}
else
{
// connecting the vertices
g[y, x] = 1;
g[x, y] = 1;
}
}
public void addVertex()
{
// increasing the number of vertices
n++;
int i;
// initializing the new elements to 0
for (i = 0; i < n; ++i)
{
g[i, n - 1] = 0;
g[n - 1, i] = 0;
}
}
public void removeVertex(int x)
{
// checking if the vertex is present
if (x > n)
{
Console.WriteLine("Vertex not present!");
return;
}
else
{
int i;
// removing the vertex
while (x < n)
{
// shifting the rows to left side
for (i = 0; i < n; ++i)
{
g[i, x] = g[i, x + 1];
}
// shifting the columns upwards
for (i = 0; i < n; ++i)
{
g[x, i] = g[x + 1, i];
}
x++;
}
// decreasing the number of vertices
n--;
}
}
}
public class GFG
{
// Driver code
public static void Main(String[] args)
{
// creating objects of class Graph
Graph obj = new Graph(4);
// calling methods
obj.addEdge(0, 1);
obj.addEdge(0, 2);
obj.addEdge(1, 2);
obj.addEdge(2, 3);
// the adjacency matrix created
obj.displayAdjacencyMatrix();
// adding a vertex to the graph
obj.addVertex();
// connecting that vertex to other existing vertices
obj.addEdge(4, 1);
obj.addEdge(4, 3);
// the adjacency matrix with a new vertex
obj.displayAdjacencyMatrix();
// removing an existing vertex in the graph
obj.removeVertex(1);
// the adjacency matrix after removing a vertex
obj.displayAdjacencyMatrix();
}
}
// This code is contributed by PrinciRaj1992
Javascript
<script>
// Javascript program to add and remove Vertex in Adjacency Matrix
class Graph
{
// constructor
constructor(x)
{
// number of vertices
this.n=x;
// adjacency matrix
this.g = new Array(10);
for(let i=0;i<10;i++)
{
this.g[i]=new Array(10);
for(let j=0;j<10;j++)
{
this.g[i][j]=0;
}
}
}
displayAdjacencyMatrix()
{
document.write("<br><br> Adjacency Matrix:");
// displaying the 2D array
for (let i = 0; i < this.n; ++i)
{
document.write("<br>");
for (let j = 0; j < this.n; ++j)
{
document.write(" " + this.g[i][j]);
}
}
}
addEdge(x,y)
{
// checks if the vertex exists in the graph
if ((x >= this.n) || (y > this.n))
{
document.write("Vertex does not exists!<br>");
}
// checks if the vertex is connecting to itself
if (x == y)
{
document.write("Same Vertex!<br>");
}
else
{
// connecting the vertices
this.g[y][x] = 1;
this.g[x][y] = 1;
}
}
addVertex()
{
// increasing the number of vertices
this.n++;
let i;
// initializing the new elements to 0
for (i = 0; i < this.n; ++i)
{
this.g[i][this.n - 1] = 0;
this.g[this.n - 1][i] = 0;
}
}
removeVertex(x)
{
// checking if the vertex is present
if (x > this.n)
{
document.write("Vertex not present!<br>");
return;
}
else
{
let i;
// removing the vertex
while (x < this.n)
{
// shifting the rows to left side
for (i = 0; i < this.n; ++i)
{
this.g[i][x] = this.g[i][x + 1];
}
// shifting the columns upwards
for (i = 0; i < this.n; ++i)
{
this.g[x][i] = this.g[x + 1][i];
}
x++;
}
// decreasing the number of vertices
this.n--;
}
}
}
// creating objects of class Graph
let obj = new Graph(4);
// calling methods
obj.addEdge(0, 1);
obj.addEdge(0, 2);
obj.addEdge(1, 2);
obj.addEdge(2, 3);
// the adjacency matrix created
obj.displayAdjacencyMatrix();
// adding a vertex to the graph
obj.addVertex();
// connecting that vertex to other existing vertices
obj.addEdge(4, 1);
obj.addEdge(4, 3);
// the adjacency matrix with a new vertex
obj.displayAdjacencyMatrix();
// removing an existing vertex in the graph
obj.removeVertex(1);
// the adjacency matrix after removing a vertex
obj.displayAdjacencyMatrix();
// This code is contributed by rag2127
</script>
Producción:
Adjacency Matrix: 0 1 1 0 1 0 1 0 1 1 0 1 0 0 1 0 Adjacency Matrix: 0 1 1 0 0 1 0 1 0 1 1 1 0 1 0 0 0 1 0 1 0 1 0 1 0 Adjacency Matrix: 0 1 0 0 1 0 1 0 0 1 0 1 0 0 1 0
Las arrays de adyacencia desperdician mucho espacio de memoria. Tales arrays resultan ser muy escasas. Esta representación requiere espacio para n*n elementos, la complejidad temporal del método addVertex() es O(n) y la complejidad temporal del método removeVertex() es O(n*n) para un gráfico de n vértices.
De la salida del programa, la array de adyacencia es:
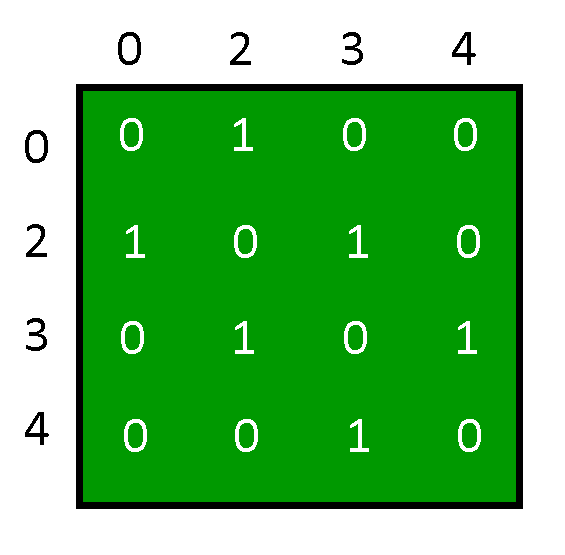
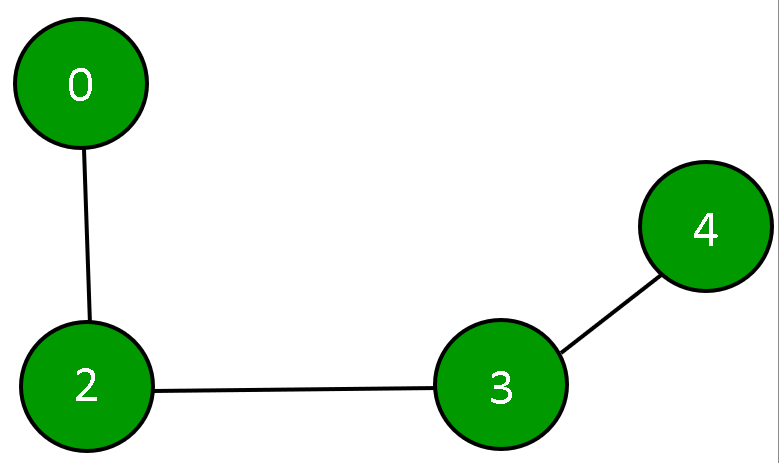
Y el gráfico representado por la array de adyacencia anterior es:
Publicación traducida automáticamente
Artículo escrito por riturajsaha y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA