MATLAB: filtro de paso bajo de Butterworth en el procesamiento de imágenes

En el campo del procesamiento de imágenes, el filtro de paso bajo Butterworth (BLPF) se utiliza para suavizar imágenes en el dominio de la frecuencia. Elimina el ruido de alta frecuencia de una imagen digital y conserva los componentes de baja frecuencia. La función de transferencia de BLPF de orden se define como-

Donde,

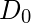• es una constante positiva. BLPF pasa todas las frecuencias menores que el 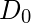valor sin atenuación y corta todas las frecuencias mayores que él.
• Este 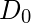es el punto de transición entre H(u, v) = 1 y H(u, v) = 0, por lo que se denomina frecuencia de corte . Pero en lugar de hacer un corte agudo (como el filtro de paso bajo ideal (ILPF) ), introduce una transición suave de 1 a 0 para reducir los artefactos de timbre.
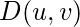• es la distancia euclidiana desde cualquier punto (u, v) al origen del plano de frecuencia, es decir,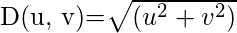

Enfoque:
Paso 1: Entrada – Leer una imagen
Paso 2: Guardar el tamaño de la imagen de entrada en píxeles
Paso 3: Obtener la transformada de Fourier de la imagen de entrada
Paso 4: Asignar el orden y la frecuencia de corte
Paso 5: Diseñar el filtro: Butterworth Filtro de paso bajo
Paso 6: Convolución entre la imagen de entrada transformada de Fourier y la máscara de filtrado
Paso 7: Tomar la transformada inversa de Fourier de la imagen contorneada
Paso 8: Mostrar la imagen resultante como salida

Implementación en MATLAB:

% MATLAB Code | Butterworth Low Pass Filter
      
% Reading input image : input_image
input_image = imread('[name of input image file].[file format]');
  
% Saving the size of the input_image in pixels-
% M : no of rows (height of the image)
% N : no of columns (width of the image)
[M, N] = size(input_image);
  
% Getting Fourier Transform of the input_image
% using MATLAB library function fft2 (2D fast fourier transform)
FT_img = fft2(double(input_image));
  
% Assign the order value
n = 2; % one can change this value accordingly
  
% Assign Cut-off Frequency
D0 = 20; % one can change this value accordingly
  
% Designing filter
u = 0:(M-1);
v = 0:(N-1);
idx = find(u > M/2);
u(idx) = u(idx) - M;
idy = find(v > N/2);
v(idy) = v(idy) - N;
  
% MATLAB library function meshgrid(v, u) returns 
% 2D grid which contains the coordinates of vectors 
% v and u. Matrix V with each row is a copy of v 
% and matrix U with each column is a copy of u 
[V, U] = meshgrid(v, u);
  
% Calculating Euclidean Distance
D = sqrt(U.^2 + V.^2);
  
% determining the filtering mask
H = 1./(1 + (D./D0).^(2*n));
  
% Convolution between the Fourier Transformed 
% image and the mask
G = H.*FT_img;
  
% Getting the resultant image by Inverse Fourier Transform 
% of the convoluted image using MATLAB library function  
% ifft2 (2D inverse fast fourier transform)   
output_image = real(ifft2(double(G))); 
    
% Displaying Input Image and Output Image 
subplot(2, 1, 1), imshow(input_image), 
subplot(2, 1, 2), imshow(output_image, [ ]);

Imagen de entrada –

Producción:

Nota: Un filtro Butterworth de orden 1 no tiene artefacto de timbre. Generalmente, el timbre es imperceptible en filtros de orden 2. Pero puede convertirse en un factor significativo en filtros de orden superior. Para una frecuencia de corte específica, el timbre aumenta con un aumento en el orden del filtro.