Programa para calcular el area del circulo interior que pasa por el centro del circulo exterior y toca su circunferencia

Dado un círculo C1 y es un radio r1 . Y uno otro círculo C2 que pasa por el centro del círculo C1 y toca la circunferencia del círculo C1 . La tarea es encontrar el área del círculo C2 . 
Ejemplos: 
 

Input: r1 = 4
Output:Area of circle c2 = 12.56

Input: r1 = 7
Output:Area of circle c2 = 38.465

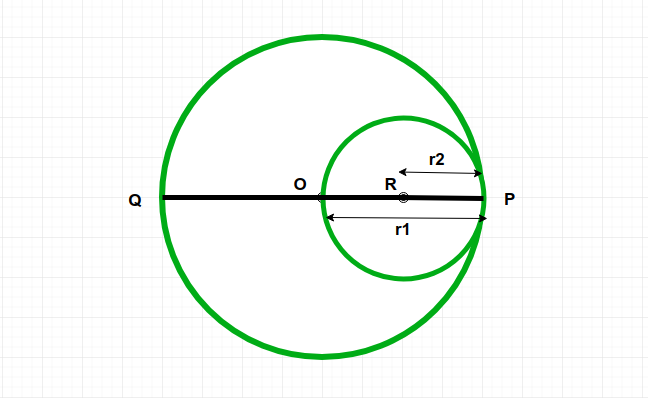
Aproximación: 
El radio r2 del círculo C2 es  . 
Entonces sabemos que el área del círculo es  .
A continuación se muestra la implementación del enfoque anterior:
 

// C++ implementation of the above approach
#include<bits/stdc++.h>
#include <iostream>
using namespace std;
 
// Function calculate the area of the inner circle
double innerCirclearea(double radius)
{
 
    // the radius cannot be negative
    if (radius < 0)
    {
        return -1;
    }
 
    // area of the circle
    double r = radius / 2;
    double Area = (3.14 * pow(r, 2));
 
    return Area;
}
 
// Driver Code
int main()
{
     
    double radius = 4;
    cout << ("Area of circle c2 = ",
                innerCirclearea(radius));
    return 0;
}
 
// This code is contributed by jit_t.

// Java implementation of the above approach
 
class GFG {
 
    // Function calculate the area of the inner circle
    static double innerCirclearea(double radius)
    {
 
        // the radius cannot be negative
        if (radius < 0) {
            return -1;
        }
 
        // area of the circle
        double r = radius / 2;
        double Area = (3.14 * Math.pow(r, 2));
 
        return Area;
    }
 
    // Driver Code
    public static void main(String arr[])
    {
        double radius = 4;
        System.out.println("Area of circle c2 = "
                           + innerCirclearea(radius));
    }
}

# Python3 implementation of the above approach
 
# Function calculate the area of the inner circle
def innerCirclearea(radius) :
 
    # the radius cannot be negative
    if (radius < 0) :
        return -1;
         
    # area of the circle
    r = radius / 2;
    Area = (3.14 * pow(r, 2));
 
    return Area;
     
# Driver Code
if __name__ == "__main__" :
     
    radius = 4;
    print("Area of circle c2 =",
           innerCirclearea(radius));
 
# This code is contributed by AnkitRai01

// C# Implementation of the above approach
using System;
     
class GFG
{
 
    // Function calculate the area
    // of the inner circle
    static double innerCirclearea(double radius)
    {
 
        // the radius cannot be negative
        if (radius < 0)
        {
            return -1;
        }
 
        // area of the circle
        double r = radius / 2;
        double Area = (3.14 * Math.Pow(r, 2));
 
        return Area;
    }
 
    // Driver Code
    public static void Main(String []arr)
    {
        double radius = 4;
        Console.WriteLine("Area of circle c2 = " +
                          innerCirclearea(radius));
    }
}
 
// This code is contributed by PrinciRaj1992

<script>
 
// JavaScript implementation of the above approach
 
// Function calculate the area of the inner circle
function innerCirclearea(radius)
{
 
    // the radius cannot be negative
    if (radius < 0)
    {
        return -1;
    }
 
    // area of the circle
    let r = radius / 2;
    let Area = (3.14 * Math.pow(r, 2));
 
    return Area;
}
 
// Driver Code
 
     
    let radius = 4;
    document.write("Area of circle c2 = " +
                innerCirclearea(radius));
 
// This code is contributed by Surbhi Tyagi.
 
</script>

Area of circle c2 = 12.56

Complejidad de tiempo: O (log r), donde r es el radio del círculo.

Espacio auxiliar: O (1), ya que no estamos usando ningún espacio adicional.