Rompecabezas: encuentra todos los valores de n > 1 para los que se puede dividir un rectángulo en n triángulos rectángulos.
Respuesta:
Podemos dividir cualquier rectángulo en n triángulos rectángulos, para cualquier n > 1 .
Hay dos métodos para dividir:
- Método 1:
- Caso 1: n = 2 , podemos obtener dos triángulos rectángulos cortando el rectángulo a lo largo de la diagonal como se muestra en la figura.
Por ejemplo: En el rectángulo ABDC, dibujamos una diagonal BC y obtenemos dos triángulos rectángulos, BDC y ABC.
- Caso 2: n > 2 , primero cortamos el rectángulo a lo largo de la diagonal y continuamos con n-2 cortes de cualquiera de los triángulos rectángulos disponibles en dos triángulos rectángulos , cortándolos a lo largo de la altura sobre su hipotenusa .
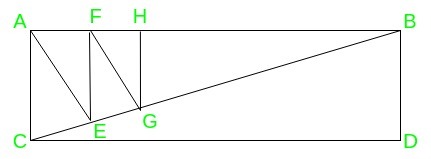
Por ejemplo: Consideremos el caso de n = 6, en el rectángulo ABDC, primero dibujamos la diagonal BC, y luego (n-2) es decir, se hacen 4 cortes en el triángulo ABC junto con la altura sobre la hipotenusa, para obtener seis correctos -triángulos angulares. Estos son BDC, ACE, AEF, FEG, FGH, HGB.
- Caso 1: n = 2 , podemos obtener dos triángulos rectángulos cortando el rectángulo a lo largo de la diagonal como se muestra en la figura.
- Método 2: También podemos resolver el acertijo considerándolo caso por caso.
- Caso 1: n es par : divide el rectángulo en n/2 rectángulos pequeños y luego puedes dividir cada uno de los rectángulos más pequeños obtenidos, a lo largo de su diagonal.
Por ejemplo: Para n=6, en el rectángulo AGHB, primero formamos 3 rectángulos más pequeños como ABCD, CEFD, EGHF. Luego, dividimos cada rectángulo por su hipotenusa BC, DE, FG respectivamente, para obtener 6 triángulos rectángulos
- Caso 2: n es impar: en este caso, primero, divida el rectángulo en n-1 triángulos pequeños utilizando el método mencionado anteriormente y luego puede cortar cualquiera de los triángulos junto con la altura en su hipotenusa.
Por ejemplo: Para n=7, primero formamos 6 triángulos como se mencionó en el punto anterior, y luego cortamos el triángulo ABC junto con la altura en su hipotenusa, para obtener el 7º triángulo AIB.
- Caso 1: n es par : divide el rectángulo en n/2 rectángulos pequeños y luego puedes dividir cada uno de los rectángulos más pequeños obtenidos, a lo largo de su diagonal.
Publicación traducida automáticamente
Artículo escrito por CharchitKapoor y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA