Método de Runge-Kutta de segundo orden para resolver ecuaciones diferenciales

Dadas las siguientes entradas:

Una ecuación diferencial ordinaria que define el valor de dy/dx en la forma x e y .
$\LARGE \frac{dy}{dx} = f(x, y)$
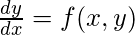
Valor inicial de y, es decir, y(0) .
$\LARGE y(0)= y_o$

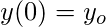
La tarea es encontrar el valor de la función desconocida y en un punto dado x, es decir, y(x) .
Ejemplo:

Entrada: x ₀ = 0, y ₀ = 1, x = 2, h = 0,2
Salida: y(x) = 0,645590
Entrada: x ₀ = 2, y ₀ = 1, x = 4, h = 0,4;
Salida: y(x) = 4.122991

Enfoque:
El método de Runge-Kutta encuentra un valor aproximado de y para una x dada. Solo las ecuaciones diferenciales ordinarias de primer orden se pueden resolver utilizando el método de segundo orden de Runge Kutta.
A continuación se muestra la fórmula utilizada para calcular el siguiente valor y _n+1 a partir del valor anterior y _n .
Por lo tanto:

y_n+1 = value of y at (x = n + 1)
y_n = value of y at (x = n)
where
  0 ≤ n ≤ (x - x₀)/h
  h is step height
  x_n+1 = x₀ + h

La fórmula esencial para calcular el valor de y(n+1):
$\LARGE K_{1} = h*f(x_{n}, y_{n})$
$\LARGE K_{2} = h*f((x_{n} + \frac{h}{2}), (y_{n} + \frac{K_{1}*h}{2}))$
$\LARGE y_{n+1} = y_{n} + K_{2} + (h^{3})$
La fórmula básicamente calcula el siguiente valor y _n+1 utilizando y _n actual más el promedio ponderado de dos incrementos:

K ₁ es el incremento basado en la pendiente al comienzo del intervalo, usando y.
K ₂ es el incremento basado en la pendiente en el punto medio del intervalo, usando (y + h*K _1/2 ) .

El método es de segundo orden, lo que significa que el error de truncamiento local es del orden de O(h ³ ), mientras que el error total acumulado es del orden de O(h ⁴ ).
A continuación se muestra la implementación del enfoque anterior:

C++

// C++ program to implement Runge
// Kutta method
#include <bits/stdc++.h>
using namespace std;
 
// A sample differential equation
// "dy/dx = (x - y)/2"
float dydx(float x, float y)
{
    return (x + y - 2);
}
 
// Finds value of y for a given x
// using step size h
// and initial value y0 at x0.
float rungeKutta(float x0, float y0,
                 float x, float h)
{
    // Count number of iterations
    // using step size or
    // step height h
    int n = (int)((x - x0) / h);
 
    float k1, k2;
 
    // Iterate for number of iterations
    float y = y0;
    for (int i = 1; i <= n; i++) {
        // Apply Runge Kutta Formulas
        // to find next value of y
        k1 = h * dydx(x0, y);
        k2 = h * dydx(x0 + 0.5 * h,
                      y + 0.5 * k1);
 
        // Update next value of y
        y = y + (1.0 / 6.0) * (k1 + 2 * k2);
 
        // Update next value of x
        x0 = x0 + h;
    }
 
    return y;
}
 
// Driver Code
int main()
{
    float x0 = 0, y = 1,
          x = 2, h = 0.2;
 
    cout << fixed << setprecision(6) << "y(x) = " << rungeKutta(x0, y, x, h);
    return 0;
}
 
// This code is contributed by shivani

C

// C program to implement Runge
// Kutta method
 
#include <stdio.h>
 
// A sample differential equation
// "dy/dx = (x - y)/2"
float dydx(float x, float y)
{
    return (x + y - 2);
}
 
// Finds value of y for a given x
// using step size h
// and initial value y0 at x0.
float rungeKutta(float x0, float y0,
                 float x, float h)
{
    // Count number of iterations
    // using step size or
    // step height h
    int n = (int)((x - x0) / h);
 
    float k1, k2;
 
    // Iterate for number of iterations
    float y = y0;
    for (int i = 1; i <= n; i++) {
        // Apply Runge Kutta Formulas
        // to find next value of y
        k1 = h * dydx(x0, y);
        k2 = h * dydx(x0 + 0.5 * h,
                      y + 0.5 * k1);
 
        // Update next value of y
        y = y + (1.0 / 6.0) * (k1 + 2 * k2);
 
        // Update next value of x
        x0 = x0 + h;
    }
 
    return y;
}
 
// Driver Code
int main()
{
    float x0 = 0, y = 1,
          x = 2, h = 0.2;
 
    printf("y(x) = %f",
           rungeKutta(x0, y, x, h));
    return 0;
}

Java

// Java program to implement Runge
// Kutta method
class GFG {
     
    // A sample differential equation
    // "dy/dx = (x - y)/2"
    static double dydx(double x, double y)
    {
        return (x + y - 2);
    }
     
    // Finds value of y for a given x
    // using step size h
    // and initial value y0 at x0.
    static double rungeKutta(double x0, double y0,
                     double x, double h)
    {
        // Count number of iterations
        // using step size or
        // step height h
        int n = (int)((x - x0) / h);
     
        double k1, k2;
     
        // Iterate for number of iterations
        double y = y0;
        for (int i = 1; i <= n; i++) {
            // Apply Runge Kutta Formulas
            // to find next value of y
            k1 = h * dydx(x0, y);
            k2 = h * dydx(x0 + 0.5 * h,
                          y + 0.5 * k1);
     
            // Update next value of y
            y = y + (1.0 / 6.0) * (k1 + 2 * k2);
     
            // Update next value of x
            x0 = x0 + h;
        }
     
        return y;
    }
     
    // Driver Code
    public static void main (String[] args)
    {
        double x0 = 0, y = 1,
              x = 2, h = 0.2;
     
        System.out.println(rungeKutta(x0, y, x, h));
    }
}
 
// This code is contributed by Yash_R

Python3

# Python3 program to implement Runge
# Kutta method
 
# A sample differential equation
# "dy/dx = (x - y)/2"
def dydx(x, y) :
 
    return (x + y - 2);
 
# Finds value of y for a given x
# using step size h
# and initial value y0 at x0.
def rungeKutta(x0, y0, x, h) :
 
    # Count number of iterations
    # using step size or
    # step height h
    n = round((x - x0) / h);
     
        # Iterate for number of iterations
    y = y0;
     
    for i in range(1, n + 1) :
         
                # Apply Runge Kutta Formulas
        # to find next value of y
        k1 = h * dydx(x0, y);
        k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1);
 
        # Update next value of y
        y = y + (1.0 / 6.0) * (k1 + 2 * k2);
 
        # Update next value of x
        x0 = x0 + h;
 
    return y;
 
# Driver Code
if __name__ == "__main__" :
 
    x0 = 0; y = 1;
    x = 2; h = 0.2;
 
    print("y(x) =",rungeKutta(x0, y, x, h));
 
# This code is contributed by Yash_R

C#

// C# program to implement Runge
// Kutta method
using System;
 
class GFG {
     
    // A sample differential equation
    // "dy/dx = (x - y)/2"
    static double dydx(double x, double y)
    {
        return (x + y - 2);
    }
     
    // Finds value of y for a given x
    // using step size h
    // and initial value y0 at x0.
    static double rungeKutta(double x0, double y0,
                     double x, double h)
    {
        // Count number of iterations
        // using step size or
        // step height h
        int n = (int)((x - x0) / h);
     
        double k1, k2;
     
        // Iterate for number of iterations
        double y = y0;
        for (int i = 1; i <= n; i++) {
            // Apply Runge Kutta Formulas
            // to find next value of y
            k1 = h * dydx(x0, y);
            k2 = h * dydx(x0 + 0.5 * h,
                          y + 0.5 * k1);
     
            // Update next value of y
            y = y + (1.0 / 6.0) * (k1 + 2 * k2);
     
            // Update next value of x
            x0 = x0 + h;
        }
     
        return y;
    }
     
    // Driver Code
    public static void Main (string[] args)
    {
        double x0 = 0, y = 1,
              x = 2, h = 0.2;
     
        Console.WriteLine(rungeKutta(x0, y, x, h));
    }
}
 
// This code is contributed by Yash_R

Javascript

<script>
 
// JavaScript program to implement Runge
// Kutta method
 
    // A sample differential equation
    // "dy/dx = (x - y)/2"
    function dydx(x, y)
    {
        return (x + y - 2);
    }
     
    // Finds value of y for a given x
    // using step size h
    // and initial value y0 at x0.
    function rungeKutta(x0, y0, x, h)
    {
        // Count number of iterations
        // using step size or
        // step height h
        let n = ((x - x0) / h);
     
        let k1, k2;
     
        // Iterate for number of iterations
        let y = y0;
        for (let i = 1; i <= n; i++) {
            // Apply Runge Kutta Formulas
            // to find next value of y
            k1 = h * dydx(x0, y);
            k2 = h * dydx(x0 + 0.5 * h,
                          y + 0.5 * k1);
     
            // Update next value of y
            y = y + (1.0 / 6.0) * (k1 + 2 * k2);
     
            // Update next value of x
            x0 = x0 + h;
        }
     
        return y;
    }
 
// Driver Code
     
    let x0 = 0, y = 1,
              x = 2, h = 0.2;
     
    document.write(rungeKutta(x0, y, x, h).toFixed(6));
   
                   
</script>

Producción:

y(x) = 0.645590

Complejidad de tiempo: O(n)

Espacio Auxiliar: O(1)

Referencia: https://en.wikipedia.org/wiki/Runge%E2%80%93Kutta_methods

Publicación traducida automáticamente

Artículo escrito por kondalalith1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

C++

C

Java

Python3

C#

Javascript

Deja una respuesta Cancelar la respuesta