¿Qué es el Mapeo de Cardinalidades? Diagramas ER

Prerrequisito: Introducción al modelo ER

Introducción:
Siempre que un atributo de un tipo de entidad se refiere a otro tipo de entidad, existe alguna relación entre ellos. 

Ejemplo –

• El atributo Gerente del departamento se refiere a un empleado que administra el departamento.
• En el modelo ER, estas referencias se representan como relaciones.

Relación:
la relación en el modelo ER se representa mediante un cuadro en forma de diamante.

Ejemplo –

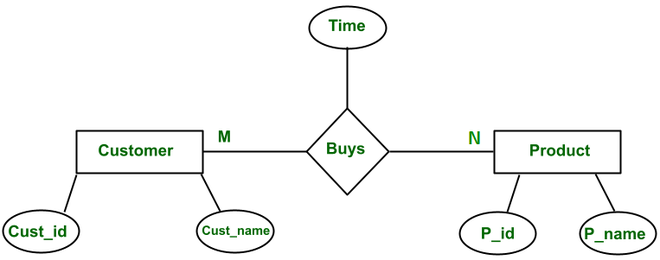
‘Compras’ es una relación entre la entidad del cliente y los productos. Esta relación se puede leer como ‘Un cliente compra un producto/productos.

Por lo tanto, una relación es una forma de conectar múltiples entidades.

• Cuando un cliente compra un producto, hay una marca de tiempo asociada a él, por lo que el atributo «Tiempo» será un atributo de «Compras».
• Todos los conceptos de la base de datos se pueden entender fácilmente a partir de los conceptos de conjuntos y relaciones.
• De acuerdo con la perspectiva de la teoría de conjuntos, se representará como

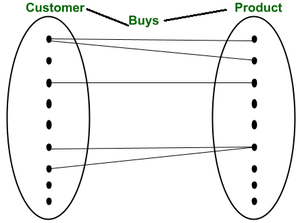
Al interpretar esto, podemos entender que muchos clientes pueden comprar el mismo tipo de producto y muchos productos pueden ser comprados por muchos clientes. Y hay algunos productos que no compra ningún cliente y hay algunos clientes que no compran ningún producto.

Según la perspectiva Relación/tabla o modelo relacional:
Se puede representar como  

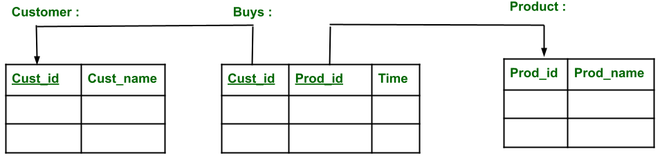
Como la relación es de muchos a muchos (M:N) entre el cliente y el producto, necesitamos tablas/relaciones separadas para ‘compras’. 
En la relación de compras, Cust_id y Prod_id son la clave externa de cliente y producto. 

Mapeo de cardinalidad/relación de cardinalidad:
La cardinalidad de mapeo es el número máximo de instancias de relación en las que una entidad puede participar.

Ejemplo –

Matemáticamente, aquí (e1, e2,e3…) son instancias de un conjunto de entidades Empleado y (d1,d2, d3….) son instancias de tipo de entidad departamento y (r1, r2, r3…) son instancias de relación de tipo de relación .

Cada instancia ri (donde _i = 1,2,3,….) en R, es una asociación de entidades, y la asociación incluye exactamente una entidad de cada tipo de entidad participante. Cada una de estas instancias de relación, ri, representa _que las entidades que participan en ri están relacionadas de alguna manera por cualquier restricción/condición proporcionada por el usuario a un diseñador.

• En el tipo de relación binaria trabaja_para Departamento: El empleado es de cardinalidad (N:1), esto significa que cada departamento puede estar relacionado con cualquier número de empleados, pero un empleado puede estar relacionado con (trabaja para) solo un departamento.
• Las posibles relaciones de cardinalidad de los tipos de relaciones binarias son (1:1, 1:N, N:1, N:M).

Restricción de participación o existencia:
Representa el número mínimo de instancias de relación en las que cada entidad puede participar y también se denomina restricción de cardinalidad mínima. Hay dos tipos de restricciones de participación, que son totales y parciales .

Ejemplo –

• En el ejemplo anterior, si la política de la empresa es que todos los empleados deben trabajar para un departamento. Luego, todos los empleados en el conjunto de entidades de empleados deben estar relacionados con el departamento mediante una relación trabaja_para. Por lo tanto, la participación del tipo de entidad empleado es total en el tipo de relación. La participación total también se llama dependencia de existencia.
• Y si hay una restricción de que un nuevo departamento no necesita tener empleados, entonces alguna entidad en el conjunto de entidades de empleados no está relacionada con la entidad del departamento por la relación trabaja_para. Por tanto, la participación de la entidad asalariada en esta relación (trabaja_para) es parcial.
• En el diagrama ER, la participación total se representa mediante una línea doble que conecta el tipo de entidad participante con la relación, y se utiliza una sola línea para la participación parcial.

La relación de cardinalidad y la restricción de participación juntas se denominan restricción estructural del tipo de relación.
Todas las relaciones de cardinalidad posibles para las relaciones binarias se explican a continuación con un ejemplo.

1. Relación uno a uno (1:1): 

Se representa usando una flecha(⇢,⇠)(Puede haber muchas notaciones posibles para el diagrama ER).
Ejemplo –

En este diagrama ER, ambas entidades, el cliente y el permiso de conducir, tienen una flecha que significa que la entidad Cliente participa en la relación «tiene un» de forma uno a uno. Podría leerse como ‘Cada cliente tiene exactamente una licencia de conducir y cada licencia de conducir está asociada con exactamente un cliente.

La perspectiva de la teoría de conjuntos del diagrama ER es

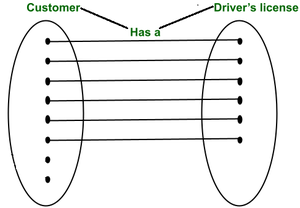
Puede haber clientes que no tengan tarjeta de crédito, pero cada tarjeta de crédito está asociada con exactamente un cliente. Por lo tanto, la entidad cliente tiene participación total en una relación.

2. Relación de uno a muchos (1:M):

Ejemplo –

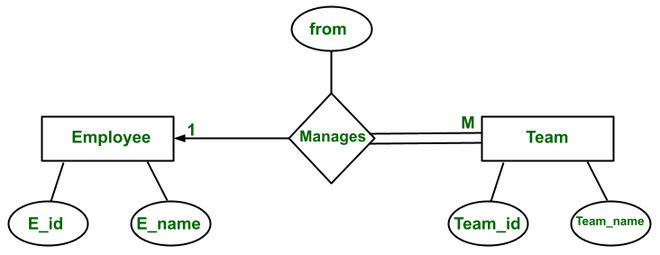
Esta relación es de uno a muchos porque “Hay algunos empleados que manejan más de un equipo mientras que solo hay un gerente para manejar un equipo”.
La perspectiva de la teoría de conjuntos del diagrama ER es:

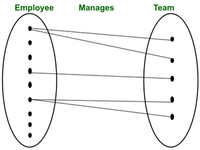
3. Relación de muchos a uno (M:1):

Ejemplo –

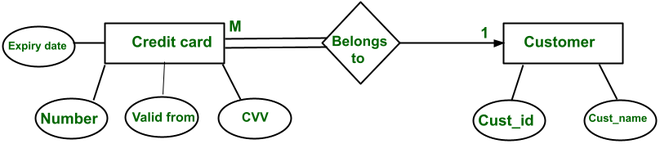
Está relacionado con una relación de uno a muchos, pero la diferencia se debe a la perspectiva.
Cualquier número de tarjetas de crédito puede pertenecer a un cliente y puede haber algunos clientes que no tengan ninguna tarjeta de crédito, pero cada tarjeta de crédito en un sistema tiene que estar asociada con un empleado (es decir, la participación total). Mientras que una sola tarjeta de crédito no puede pertenecer a varios clientes.
La perspectiva de la teoría de conjuntos del diagrama ER es:

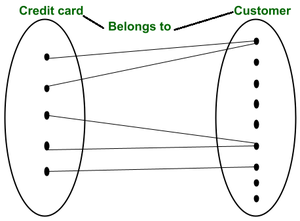
4. Relación de muchos a muchos (M:N):

Ejemplo:
un cliente puede comprar cualquier cantidad de productos y muchos clientes pueden comprar un producto. 

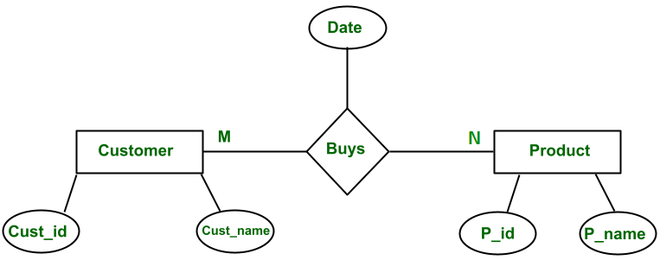
La perspectiva de la teoría de conjuntos del diagrama ER es:

Cualquiera de las cuatro cardinalidades de una relación binaria puede tener ambos lados parciales, ambos totales y una participación parcial y una total, según las restricciones especificadas por los requisitos del usuario.