Para hacer una curva de campana en R usaremos la ayuda de la distribución normal que conducirá a una curva de campana que será simétrica con respecto a la media. La mitad de los datos caerán a la izquierda de la media y la mitad a la derecha.
En la teoría de la probabilidad, una distribución normal es un tipo de distribución de probabilidad continua para una variable aleatoria de valor real.
Fórmula matemática:
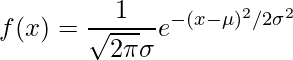
Dónde,
is mean
is standard deviation.
Para la distribución normal, usamos la función dnorm() para obtener el valor de la función de densidad de probabilidad para la distribución normal dados los parámetros para x, μ y σ.
Sintaxis: dnorm(x, mean, sd) (sd=desviación estándar)
Parámetros:-
- X es un vector de números.
- La media es el valor medio de los datos de la muestra. Su valor por defecto es cero.
- Sd es la desviación estándar. Su valor por defecto es 1.
Devoluciones:-La distribución de probabilidad en cada punto para una media y desviación estándar dadas.
Acercarse
- Crear una secuencia de números
- Obtenga la distribución de probabilidad en cada punto para una media y una desviación estándar dadas
- Trazar datos con atributos apropiados
Ejemplo 1:
R
# sequence of numbers between -10 and 10 incrementing by 0.1. x <- seq(-12, 12, by = .1) # getting probability distribution for each point y <- dnorm(x, mean = 5, sd = 1) # Plot graph plot(x,y)
Producción:
Ejemplo 2:
R
# sequence of numbers between -10 and 10 incrementing by 0.1. x <- seq(-5, 5, by = .5) # getting probability distribution y <- dnorm(x, mean = 1, sd = 1.5) # plot data plot(x,y, col="red")
Producción:
