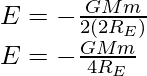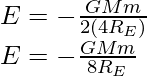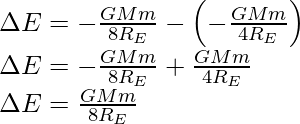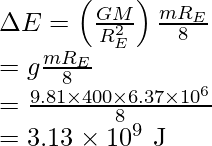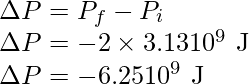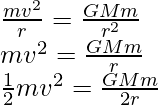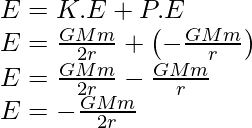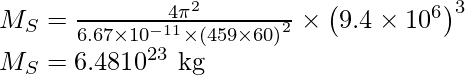Los seres humanos aprenden temprano en la vida que todos los elementos materiales tienen una tendencia natural a gravitar hacia la tierra. Todo lo que se lanza cae al suelo, viajar cuesta arriba es mucho más agotador que caminar cuesta abajo, las lluvias de las nubes caen al suelo, y hay varios ejemplos adicionales.
Los satélites de la Tierra son objetos celestes que orbitan alrededor de la Tierra. Su movimiento es similar al de las órbitas de los planetas alrededor del Sol, por lo que las reglas del movimiento planetario establecidas por Kepler son igualmente válidas y aplicables a ellos. Las órbitas de los satélites terrestres alrededor de la Tierra son circulares o elípticas. La luna es el único satélite natural de la Tierra. Muchos países, incluida la India, han podido lanzar satélites terrestres artificiales para su uso en áreas como las telecomunicaciones, la geofísica y la meteorología gracias a los avances tecnológicos.
¿Qué es la gravitación?
La gravitación, o simplemente gravedad, es la fuerza que atrae a dos cuerpos juntos. Todos los objetos del cosmos se atraen entre sí con cierto nivel de fuerza, pero debido a las grandes distancias entre los objetos, la fuerza es demasiado débil para notarse en la mayoría de las circunstancias. Además, aunque el alcance de la gravedad es infinito, el efecto se debilita a medida que los objetos se alejan más.
Energía potencial gravitatoria: La energía almacenada en el cuerpo en una determinada postura se conoce como energía potencial. Si la ubicación de una partícula cambia como resultado de las fuerzas que actúan sobre ella, el cambio en su energía potencial es igual a la cantidad de trabajo que la fuerza realiza sobre el cuerpo. La energía potencial gravitacional es la energía potencial de un cuerpo que surge de la fuerza de la gravedad. La expresión de la energía potencial entre el satélite y la tierra se puede dar como,
PE = -GMm/r
Energía de enlace de los satélites o energía de los satélites en órbita
Binding Energy es la cantidad mínima de energía que debe entregarse al satélite para liberarse de la atracción gravitacional del planeta o de la influencia gravitatoria del planeta.
El término “energía de enlace” se refiere a la energía que une el satélite a la Tierra. La atracción gravitacional entre el satélite y el planeta será superada por esta energía vinculante.
Considere un satélite que gira en una trayectoria circular alrededor de la tierra. La fuerza de atracción gravitatoria entre la Tierra y el satélite proporciona la fuerza centrípeta necesaria para mantener al satélite girando en una órbita circular estable. Hay dos tipos de energías mecánicas en el satélite mientras orbita el planeta. Debido a su movimiento orbital, existe la energía cinética y debido a su posición en el campo gravitacional de la tierra existe la energía potencial.
Derivación de la energía de enlace de los satélites

Un satélite sobre la superficie de la tierra.
Sea, la masa de la tierra es M, la masa del satélite es m, el radio de la tierra es R, la altura del satélite desde la superficie terrestre es h, el radio de la órbita circular del satélite es r o (R+h), y la velocidad crítica del satélite es v.
Una fuerza centrípeta igual a la fuerza gravitacional porque proporciona la fuerza centrípeta necesaria que se requiere para el movimiento circular, es decir
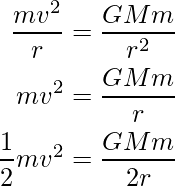
donde G es la constante gravitacional universal.
Entonces, la energía cinética se puede escribir como,
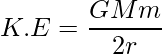
Ahora, la energía potencial entre el satélite y la tierra se puede dar como,
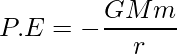
Aquí el signo negativo representa la fuerza que actúa entre el satélite y la tierra es atractiva. . Sin embargo, la magnitud de la KE es la mitad de la PE, por lo que la E total será la suma de la energía cinética y la energía potencial.
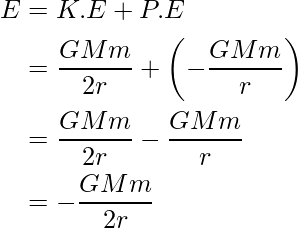
La expresión anterior es la energía de enlace del satélite que gira alrededor de la tierra en una órbita circular estable.
Expresión de la Energía de Enlace del Satélite estacionario en la superficie terrestre.
Sea, la masa del satélite estacionario es m, por lo tanto la energía cinética es igual a cero.
Ahora, la energía potencial se puede expresar como,
![]()
La E total será la suma de la energía cinética y la energía potencial,
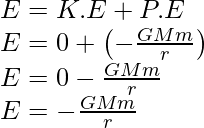
Aquí el signo negativo representa la fuerza que actúa entre el satélite y la tierra es atractiva.
Satélites de la Tierra
Los satélites terrestres son cuerpos celestes que orbitan alrededor de la tierra. El movimiento de los cuerpos celestes es muy parecido al movimiento de los planetas que orbitan alrededor del Sol y, por lo tanto, las leyes del movimiento planetario de Kepler también se aplican a ellos. En general, las órbitas de los satélites terrestres son circulares o elípticas. La luna es el único satélite natural de la tierra con una órbita casi circular y un período de tiempo de alrededor de 27,3 días, que es casi equivalente al período de rotación de la luna alrededor de su propio eje.
Sea un satélite en una órbita circular a una distancia (R E + h) del centro de la tierra, donde R E es el radio de la tierra. Si m es la masa del satélite, entonces la velocidad del satélite viene dada por
![]()
En cada órbita, el satélite recorre una distancia 2π(R E + h) con velocidad V. Su período de tiempo T viene dado por
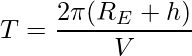
Sustituye el valor de V en la expresión anterior,
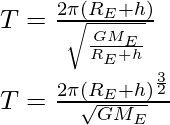
Ingravidez
La fuerza con la que la tierra atrae un objeto se llama peso. Cuando nos paramos sobre una superficie, somos conscientes de nuestro propio peso porque la superficie ejerce una fuerza opuesta para mantenernos en reposo. Cuando usamos una balanza de resorte suspendida de una posición fija, como el techo, para determinar el peso de un objeto, se aplica el mismo principio. A menos que esté sujeto a una fuerza que se oponga a la gravedad, el objeto caerá. El resorte aplica exactamente esta fuerza sobre el objeto. Esto se debe a que la atracción gravitacional del objeto tira del resorte un poco hacia abajo, y el resorte ejerce una fuerza verticalmente hacia arriba sobre el objeto.
Imagine que el extremo superior de la balanza ya no está unido al techo superior de la habitación. El objeto, así como ambos extremos del resorte, se mueven con la misma aceleración g. El resorte no está extendido y no ejerce ninguna fuerza hacia arriba sobre el objeto, que cae en g debido a la gravedad. Debido a que el resorte no está extendido en absoluto, la lectura de la balanza de resorte es cero. Debido a que no hay fuerza hacia arriba sobre el objeto, si fuera un ser humano, él o ella no sentiría su peso. Como resultado, cuando un objeto está en caída libre, no tiene peso, y este fenómeno se conoce como ingravidez.

Cada porción y parcela de un satélite que orbita alrededor de la tierra tiene una aceleración hacia el centro de la tierra igual al valor de la aceleración de la tierra debido a la gravedad en ese lugar. Como resultado, todo dentro del satélite está en caída libre. Es como si un humano cayera desde una gran altura hacia el suelo. Como resultado, los humanos dentro de un satélite no tienen sentido de la gravedad. Debido a que la gravedad define la dirección vertical para los humanos, no tienen direcciones horizontales ni verticales; todas las direcciones son las mismas para ellos. Así lo demuestran las imágenes de astronautas flotando en el espacio en un satélite.
Ejemplos de preguntas
Problema 1: Un satélite de 400 kg se encuentra en una órbita circular de radio 2R E alrededor de la Tierra. ¿Cuánta energía se requiere para transferirlo a una órbita circular de radio 4R E ? ¿Cuáles son los cambios en las energías cinética y potencial?
Solución:
Dado,
La masa del satélite es de 400 kg.
El radio inicial de la órbita es 2R E .
El radio final de la órbita es 4R E .
La expresión para la energía de enlace es,
,
Entonces, la energía de enlace del satélite en un radio de órbita 2R E es
entonces, la energía de enlace del satélite en un radio de órbita 4R E es
El cambio en la energía de enlace de energía total es
Sustituya la energía inicial y final en la expresión anterior,
Reorganizar la expresión y sustituir todos los valores,
La energía cinética se reduce y es igual a menos de ∆E,
Y el cambio en la energía potencial es el doble del cambio en la energía de enlace,
Problema 2: Definir la energía de enlace del satélite y derivar su expresión.
Solución:
Binding Energy es la cantidad mínima de energía que debe entregarse al satélite para liberarse de la atracción gravitacional del planeta o de la influencia gravitacional del planeta. El término “energía de enlace” se refiere a la energía que une el satélite a la Tierra. Esta energía superará la fuerza de atracción gravitacional entre el satélite y la Tierra.
Sea, la masa de la tierra es M, la masa del satélite es m, el radio de la tierra es R, la altura del satélite desde la superficie terrestre es h, el radio de la órbita circular del satélite es r o (R+h), y la velocidad crítica del satélite es v.
La fuerza gravitacional proporciona la fuerza centrípeta necesaria para el movimiento circular. Entonces, una fuerza centrípeta igual a la fuerza gravitacional, es decir
donde G es la constante gravitacional universal.
Entonces, la energía cinética se puede escribir como,
Ahora, la energía potencial entre el satélite y la tierra se puede dar como,
Aquí el signo negativo representa la fuerza que actúa entre el satélite y la tierra es atractiva. . Sin embargo, la magnitud de la KE es la mitad de la PE, por lo que la E total será la suma de la energía cinética y la energía potencial.
La expresión anterior es la energía de enlace del satélite que gira alrededor de la tierra en una órbita circular estable.
Problema 3: ¿Qué es la ley de gravitación universal de Newton?
Solución:
Cada partícula del universo atrae a todas las demás partículas con una fuerza proporcional al producto de sus masas e inversamente proporcional al cuadrado de su distancia.
De acuerdo con la ley, una fuerza que actúa a lo largo de la línea que conecta los dos puntos atrae a cualquier otra masa puntual, . La fuerza es proporcional al producto de las dos masas, y es inversamente proporcional al cuadrado de su distancia.
donde F es la fuerza gravitacional que actúa entre dos objetos, M y m son las masas de los objetos, r es la distancia entre los centros de sus masas y G es la constante gravitatoria.
Problema 4: Enunciar las leyes de movimiento planetario de Kepler.
Solución:
Las leyes de movimiento planetario de Kepler establecen que:
- El Sol está en uno de los puntos focales de las órbitas elípticas, que siguen todos los planetas.
- El radio vector dibujado desde el Sol hasta un planeta cubre la misma área en la misma cantidad de tiempo. Debido a esto, la fuerza gravitacional del planeta es central, por lo que se conserva el momento angular.
- El cuadrado del período orbital de un planeta es proporcional al cubo del semieje mayor de la órbita elíptica del planeta. El periodo T y el radio R de la órbita circular de un planeta alrededor del Sol están relacionados por
donde Ms es la masa del Sol. La mayoría de los planetas tienen órbitas casi circulares alrededor del Sol. Para órbitas elípticas, la ecuación anterior es válida si R se reemplaza por el semieje mayor, a.
Problema 5: El planeta Marte tiene dos lunas, Fobos y Delmos. Fobos tiene un período de 7 horas, 39 minutos y un radio orbital de 9,4 × 10 3 km. Calcular la masa de Marte.
Solución:
Dado,
El tiempo es igual a 7 horas, 39 minutos, es decir, 459 min y esto es igual a (459×60) seg.
Un radio orbital es 9,4 × 10 3 km, es decir, 9,4 × 10 6 m.
Según las leyes de Kepler
Reorganizar la expresión anterior,
Sustituya los valores en la expresión anterior,
Publicación traducida automáticamente
Artículo escrito por anoopraj758 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA