Eliminación de la ambigüedad (Conversión de una gramática ambigua en una gramática inequívoca)

Requisitos previos: Gramáticas libres de contexto , Gramática ambigua , Diferencia entre gramática ambigua y no ambigua, Precedencia y asociatividad de operadores , Gramática recursiva
En este artículo vamos a ver la eliminación de la ambigüedad de la gramática usando ejemplos adecuados.

Gramática ambigua vs inequívoca:
las gramáticas que tienen más de un árbol de derivación o árbol de análisis son gramáticas ambiguas. Esta gramática no es analizada por ningún analizador .

Ejemplo :
1. Considere la producción que se muestra a continuación:

S->aSbS | bSaS | ∈

Digamos que queremos generar la string «abab» a partir de la gramática anterior. Podemos observar que la string dada se puede derivar usando dos árboles de análisis. Entonces, la gramática anterior es ambigua.

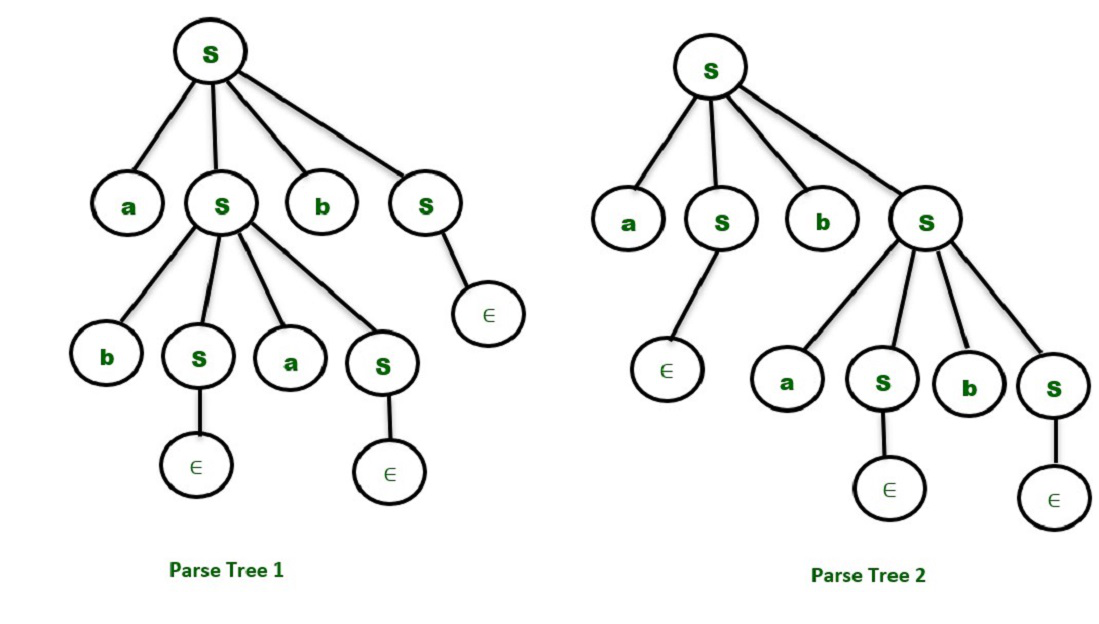
Las gramáticas que tienen un solo árbol de derivación o árbol de análisis sintáctico se denominan gramáticas unívocas.

 2. Considere las producciones que se muestran a continuación:

S -> AB
A -> Aa | a
B -> b

Para la string «aab» solo tenemos un árbol de análisis para la gramática anterior, como se muestra a continuación.

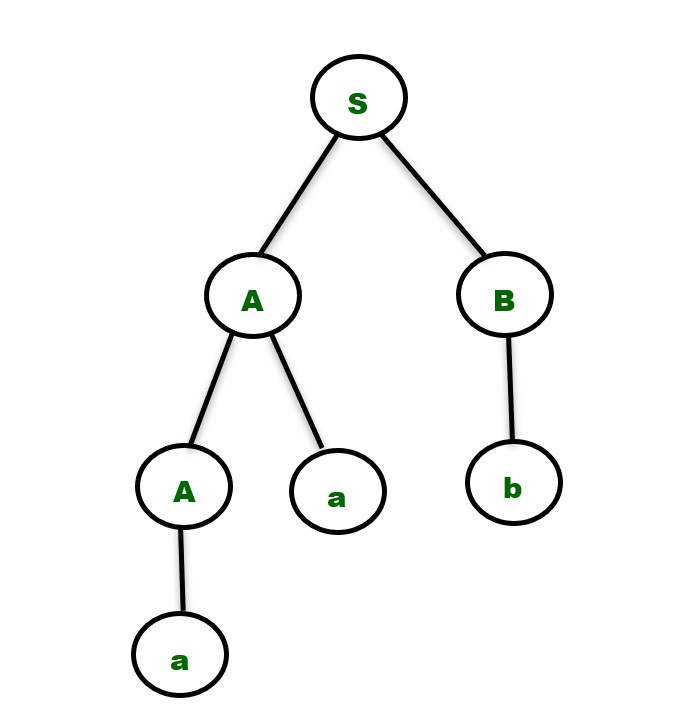
Es importante tener en cuenta que no existen algoritmos directos para encontrar si la gramática es ambigua o no. Necesitamos construir el árbol de análisis para una string de entrada dada que pertenece al lenguaje producido por la gramática y luego decidir si la gramática es ambigua o inequívoca en función de la cantidad de árboles de análisis obtenidos como se discutió anteriormente.

Nota: la string debe elegirse con cuidado porque puede haber algunas strings disponibles en el idioma producido por la gramática inequívoca que tiene solo un árbol de análisis.

Eliminación de la ambigüedad:
podemos eliminar la ambigüedad únicamente sobre la base de las siguientes dos propiedades:

1. Precedencia: 
si se utilizan diferentes operadores, consideraremos la precedencia de los operadores. Las tres características importantes son:

1. El nivel al que está presente la producción denota la prioridad del operador utilizado.
2. La producción a niveles más altos tendrá operadores con menor prioridad . En el árbol de análisis, los Nodes que se encuentran en los niveles superiores o cerca del Node raíz contendrán los operadores de menor prioridad.
3. La producción en los niveles inferiores tendrá operadores con mayor prioridad . En el árbol de análisis, los Nodes que se encuentran en niveles más bajos o cerca de los Nodes hoja contendrán los operadores de mayor prioridad.

2. Asociatividad:
si los mismos operadores de precedencia están en producción, entonces tendremos que considerar la asociatividad.

• Si la asociatividad es de izquierda a derecha, entonces tenemos que provocar una recursión a la izquierda en la producción. El árbol de análisis también se dejará recursivo y crecerá en el lado izquierdo. 
  +, -, *, / son operadores asociativos a la izquierda.
• Si la asociatividad es de derecha a izquierda, entonces tenemos que provocar la recursión a la derecha en las producciones. El árbol de análisis también será recursivo a la derecha y crecerá en el lado derecho. 
  ^ es un operador asociativo derecho.

Ejemplo 1 – Considere la gramática ambigua

E -> EE | id
El lenguaje en la gramática contendrá { id, id-id, id-id-id, ….}

Digamos que queremos derivar la string id-id-id. Consideremos un solo valor de id=3 para obtener más información. El resultado debería ser:

3-3-3 =-3 
Dado que los mismos operadores de prioridad, debemos considerar la asociatividad que es de izquierda a derecha.

Árbol de análisis: el árbol de análisis que crece en el lado izquierdo de la raíz será el árbol de análisis correcto para que la gramática no sea ambigua.

Entonces, para que la gramática anterior no sea ambigua, simplemente haga que la gramática sea recursiva a la izquierda reemplazando la E no terminal más a la izquierda en el lado derecho de la producción con otra variable aleatoria, digamos P. La gramática se convierte en:

E -> E – P | P
P -> identificación

La gramática anterior ahora no es ambigua y contendrá solo un árbol de análisis para la expresión anterior, como se muestra a continuación:

De manera similar, la gramática inequívoca para la expresión: 2^3^2 será:

mi -> pag^ mi | P // Derecho Recursivo ya que ^ es asociativo derecho.
P -> identificación

Ejemplo 2: considere la gramática que se muestra a continuación, que tiene dos operadores diferentes:

E -> E + E | mi * mi | identificación

Claramente, la gramática anterior es ambigua ya que podemos dibujar dos árboles de análisis para la string «id+id*id» como se muestra a continuación. Considere la expresión:

3 + 2 * 5 // “*” tiene más prioridad que “+”
La respuesta correcta es: (3+(2*5))=13

El “+” que tiene la menor prioridad tiene que estar en el nivel superior y tiene que esperar el resultado producido por el operador “*” que está en el nivel inferior. Entonces, el primer árbol de análisis es el correcto y da el mismo resultado esperado.

La gramática unívoca contendrá las producciones que tengan el operador de mayor prioridad («*» en el ejemplo) en el nivel inferior y viceversa. La asociatividad de ambos operadores es de izquierda a derecha . Entonces, la gramática unívoca tiene que ser recursiva. La gramática será:

E -> E + P            // + está en un nivel superior y asociativo a la izquierda
E -> P 
P -> P * Q           // * está en un nivel inferior y asociativo a la izquierda
P -> Q  
Q -> id

  (o)

E -> E + P | P
P -> P * Q | Q
Q -> identificación

E se usa para realizar operaciones de suma y P se usa para realizar operaciones de multiplicación. Son independientes y mantendrán el orden de precedencia en el árbol de análisis.
El árbol de análisis para la string «id+id*id+id» será:

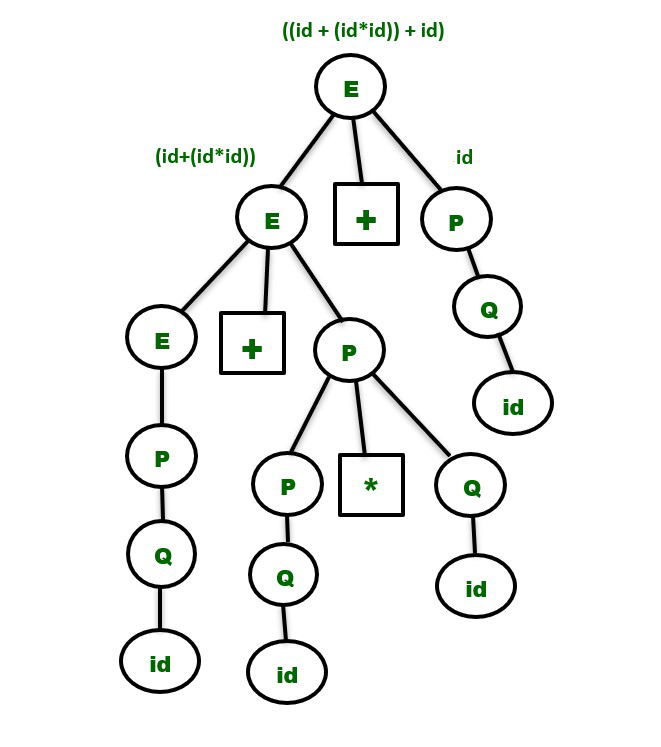
Nota: es muy importante tener en cuenta que al convertir una gramática ambigua en una gramática inequívoca, no debemos cambiar el idioma original proporcionado por la gramática ambigua. Por lo tanto, los no terminales en la gramática ambigua tienen que ser reemplazados con otras variables de tal manera que obtengamos el mismo lenguaje que se derivó antes y también mantengamos la precedencia y la regla de asociatividad simultáneamente.

Esta es la razón por la que escribimos la producción E -> P y P -> Q y Q -> id después de reemplazarlos en el ejemplo anterior, porque el idioma también contiene las strings { id, id+id } .
De manera similar, la gramática inequívoca para una expresión que tiene los operadores -,*,^ es:

E -> E – P | P                    // El operador menos está en un nivel más alto debido a la menor prioridad y asociativo a la izquierda.
P -> P * Q | Q                 // El operador de multiplicación tiene más prioridad que – y menos que ^ y asociativo a la izquierda.
Q -> R ^ Q | R              // El operador exponente está en un nivel más bajo debido a la prioridad más alta y la asociatividad correcta.
R -> identificación

Además, hay algunas gramáticas ambiguas que no se pueden convertir en gramáticas unívocas.