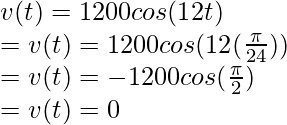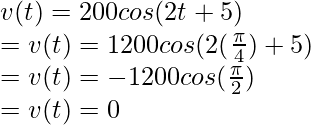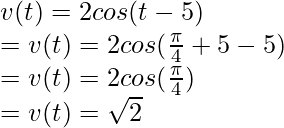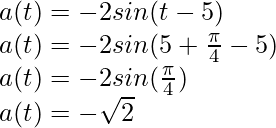Velocidad y aceleración en movimiento armónico simple

El movimiento armónico simple es un movimiento periódico que se repite después de un cierto período de tiempo. Se puede ver en casi todas partes en la vida real, por ejemplo, un cuerpo conectado a un resorte está haciendo un movimiento armónico simple. Es esencial conocer la ecuación para la posición, velocidad y aceleración del objeto. Estas ecuaciones nos ayudan a deducir información sobre el objeto del SHM y predecir su comportamiento. Veamos cómo extraer esta información de un SHM en detalle.

Movimiento periódico y oscilatorio

Considere un ejemplo de un insecto que intenta trepar por la pared, este insecto sube a una altura y luego vuelve a caer. Tenga en cuenta que el movimiento de este insecto se repite después de un tiempo. Este tipo de movimiento se llama movimiento periódico. Un movimiento periódico se repite después de un cierto intervalo de tiempo. En la figura, se muestran algunos gráficos que representan un movimiento periódico. El gráfico tiene un patrón que se repite, lo que significa que la posición y del objeto aumenta y luego disminuye periódicamente.

Los movimientos periódicos y oscilatorios pueden parecer lo mismo, pero tienen una pequeña diferencia. Todo movimiento oscilatorio es un movimiento periódico, pero no al revés. Los movimientos periódicos simplemente se repiten después de un cierto intervalo de tiempo, pero los movimientos oscilatorios se mueven de un lado a otro alrededor de una posición media. El movimiento armónico simple es el tipo más simple de movimiento oscilatorio.

Movimiento armónico simple

El movimiento armónico simple es un tipo de movimiento periódico en el que el objeto se mueve de un lado a otro alrededor de su posición media. Este movimiento surge cuando la fuerza que actúa sobre el cuerpo es directamente proporcional al desplazamiento del cuerpo desde su posición media. El período de tiempo, en este caso, permanece constante. El período de tiempo se denota por «T» y la distancia de la posición media desde la posición extrema se llama amplitud, se denota por A. Un péndulo oscilante es un ejemplo de movimiento armónico simple.

La ecuación general para el desplazamiento (x) del objeto en cualquier momento particular está dada por,

$x = A sin(\omega t + \phi)$

Aquí, $\omega = \frac{2 \pi}{T}$ y $\phi$ denota el cambio de fase.

De manera similar, la ecuación para la velocidad del objeto en SHM se puede encontrar derivando esta ecuación.

$v = A\omega cos(\omega t + \phi)$

Entonces, la ecuación para la aceleración se convierte en,

$a = -A\omega^2 sin(\omega t + \phi)$

Observe en la figura anterior que los tres valores de desplazamiento, velocidad y aceleración en SHM tienen el mismo período de tiempo que SHM, pero tienen una fase de 90° entre cada uno de ellos.

Problemas de muestra

Pregunta 1: La ecuación para el SHM se da a continuación.

x(t) = 5 cos(2t)

Calcular la aceleración y la velocidad máximas.

Responder:

La ecuación general de SHM está dada por,

$x = A sin(\omega t + \phi)$

En este caso, A = 5, $\omega = 2$

La velocidad máxima será,

$v = A\omega$

⇒ v = (5)(2)

⇒ v = 10 m/s

La aceleración máxima será,

$a = -A\omega^2$

⇒ un = – (5)(2) ²

⇒ a = -20 m/ ^s2

Pregunta 2: La ecuación para el SHM se da a continuación.

x(t) = 10sen(5t)

Calcular la aceleración y la velocidad máximas.

Responder:

La ecuación general de SHM está dada por,

$x = A sin(\omega t + \phi)$

En este caso, A = 10, $\omega = 5$

La velocidad máxima será,

$v = A\omega$

⇒ v = (10)(5)

⇒ v = 50 m/s

La aceleración máxima será,

$a = -A\omega^2$

⇒ un = – (10)(5) ²

⇒ a = -250 m/ ^s2

Pregunta 3: La ecuación para el SHM se da a continuación.

x(t) = 100sen(12t)

Calcular el tiempo y la velocidad en t = $\frac{\pi}{24}$

Responder:

La ecuación general de SHM está dada por,

$x = A sin(\omega t + \phi)$

En este caso, A = 100, $\omega = 12$

Sabemos,

$\omega = \frac{2\pi}{T}$

Reemplazando los valores en la ecuación,

$12 = \frac{2\pi}{T}$

⇒ $T = \frac{\pi}{6}$

La ecuación para la velocidad se encontrará derivando la ecuación dada,

x(t) = 100sen(12t)

⇒ $\frac{d}{dt}(x(t)) = \frac{d}{dt}(100sin(12t) )$

⇒ $v(t) = 1200cos(12t)$

en t = $\frac{\pi}{24}$

$v(t) = 1200cos(12t) \\ = v(t) = 1200cos(12(\frac{\pi}{24})) \\ = v(t) = -1200cos(\frac{\pi}{2}) \\ = v(t) = 0$

Pregunta 4: La ecuación para el SHM se da a continuación.

x(t) = 100sen(2t + 5)

Calcular el tiempo y la velocidad en t = $\frac{\pi}{2}$

Responder:

La ecuación general de SHM está dada por,

$x = A sin(\omega t + \phi)$

En este caso, A = 100, $\omega = 2$

Sabemos,

$\omega = \frac{2\pi}{T}$

Reemplazando los valores en la ecuación,

$2 = \frac{2\pi}{T}$

⇒ $T = \pi$

La ecuación para la velocidad se encontrará derivando la ecuación dada,

x(t) = 100sen(2t + 5)

⇒ $\frac{d}{dt}(x(t)) = \frac{d}{dt}(100sin(2t + 5) )$

⇒ $v(t) = 200cos(2t + 5)$

en t = $\frac{\pi}{2}$

$v(t) = 200cos(2t + 5) \\ = v(t) = 1200cos(2(\frac{\pi}{4}) + 5) \\ = v(t) = -1200cos(\frac{\pi}{2}) \\ = v(t) = 0$

Pregunta 5: La ecuación para el SHM se da a continuación.

x(t) = 2sen(t – 5)

Calcular el período de tiempo, la aceleración y la velocidad en t = $5 + \frac{\pi}{4}$

Responder:

La ecuación general de SHM está dada por,

$x = A sin(\omega t + \phi)$

En este caso, A = 2, $\omega = 1$

Sabemos,

$\omega = \frac{2\pi}{T}$

Reemplazando los valores en la ecuación,

$1 = \frac{2\pi}{T}$

⇒ $T = 2\pi$

Las ecuaciones para la velocidad y las aceleraciones se encontrarán derivando la ecuación dada,

x(t) = 2sen(t – 5)

⇒ $\frac{d}{dt}(x(t)) = \frac{d}{dt}(2sin(t - 5) )$

⇒ $v(t) = 2cos(t - 5)$

en t = $\frac{\pi}{4} + 5$

$v(t) = 2cos(t - 5) \\ = v(t) = 2cos(\frac{\pi}{4} + 5 - 5) \\ = v(t) = 2cos(\frac{\pi}{4}) \\ = v(t) = \sqrt{2}$

$v(t) = 2cos(t - 5)$

⇒ $\frac{d}{dt}(v(t)) = \frac{d}{dt}(2cos(t - 5) )$

⇒ a(t) = -2sen(t – 5)

en t = $\frac{\pi}{4} + 5$

$a(t) = -2sin(t - 5) \\ a(t) = -2sin(5 + \frac{\pi}{4} - 5) \\ a(t) = -2sin(\frac{\pi}{4}) \\ a(t) = -\sqrt{2}$