Refracción de la luz a través de losa de vidrio

Losa de vidrio es una sustancia o lámina hecha de un material de vidrio que tiene 3 dimensiones que son largo ancho y alto, tiene forma de cuboide. No desvía ni dispersa los rayos de luz que lo atraviesan. Esto significa que el rayo incidente y el emergente que sale de la losa de vidrio son paralelos. La losa de vidrio solo y solo produce un cambio o desplazamiento lateral o (hacia los lados) en la dirección de la luz.

Como podemos observar y ver a continuación, la refracción o curvatura de los rayos de luz a través de una losa de vidrio tiene lugar en las dos superficies paralelas, iguales y opuestas. Como podemos ver y observar el rayo incidente que incide sobre una de las superficies paralelas de la losa primero sufre refracción en la superficie PS y el rayo refractado se desvía hacia la normal, y nuevamente incide en la otra superficie que es igual a la el primero y ese es QR. A través de una losa de vidrio, la luz antes de volver al aire sufre refracción dos veces. En la segunda vez, el rayo refractado se desvía de la normal. Si la luz incide en ángulo recto, atravesará la losa de vidrio sin ninguna desviación. El rayo emergente como podemos ver ha emergido paralelo al anterior a un rayo de luz incidente.

Ahora podemos rastrear fácilmente el rayo de luz después de pasar a través de la losa de vidrio de la siguiente manera:

Términos relacionados

Rayo incidente : el rayo de luz que cae oblicuamente sobre una de las superficies de la losa de vidrio se conoce o se denomina rayo incidente. Podemos usar muchas fuentes de luz para generar rayos incidentes para observar la refracción que ocurre a través de una losa de vidrio.

Rayo refractado : el rayo de luz que emerge después de la refracción a través de una de las superficies en las que ha incidido el rayo incidente. El rayo refractado se mueve hacia lo normal en caso de que la luz entre desde un medio más raro a uno más denso, o se aleja más del rayo normal en caso de que la luz viaje de un medio más denso a uno más raro.

Rayo normal: se dibujan dos rayos normales en las dos superficies paralelas opuestas de la losa desde donde medimos los ángulos de incidencia, refracción y emergencia, respectivamente.

Rayo emergente : el rayo de luz que emerge de otra cara opuesta de la losa de vidrio se denomina rayo emergente. Se ha visto u observado que el rayo emergente emerge algo paralelo al camino de donde podría haber emergido el rayo incidente si no hubiera experimentado ningún cambio.

Desplazamiento lateral

Hay una distancia entre el incidente y el rayo emergente que emergió. Esta distancia se conoce como desplazamiento lateral o desplazamiento. Lo consideramos un cambio del camino original de donde se suponía que el rayo de luz incidente emergería si no hubiera experimentado o sufrido refracción alguna. Cuanto más gruesa es la losa de vidrio, más desplazamiento o desplazamiento se observa desde la posición incidente original.

Depende del espesor de la losa de vidrio dada y del ángulo de incidencia y refracción respectivamente. La fórmula del desplazamiento lateral se da a continuación:

$l = t \frac{sin(i-r)} {cosr}$

Donde i = ángulo de incidencia

r = ángulo de refracción

t = espesor de la losa de vidrio dada

l = desplazamiento lateral o desplazamiento

Leyes de la refracción

Con base en la refracción a través de diferentes superficies, se observaron algunas propiedades comunes en todos. Se dan dos leyes de refracción como se dan y se establecen a continuación, a la vista de la refracción, la luz sigue y lo que vemos es la imagen refractada formada del objeto.

El rayo refractado desde la superficie, incidente o lo que llamamos rayo que cae oblicuamente, y el rayo normal en el punto de incidencia tenderán todos a estar juntos en el mismo plano.
Tenemos la relación del seno del ángulo de incidencia y refracción es una constante o tiene un valor definido. Lo cual se enuncia como la ley de Snell .
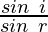$\frac{sin \ i} {sin \ r}$ = constante
Donde tenemos i = ángulo de incidencia, r = ángulo de refracción, el valor constante que depende de los índices de refracción de los dos medios tomados. Es su proporción y es adimensional.

Problemas de muestra

Pregunta 1: ¿Cuál es el valor constante si el ángulo de refracción es de 15° y el ángulo de incidencia es de 35°?

Solución:

Como la conocemos,

$\frac{sin(i)}{sin(r)}$ = constante

Dado sen i = sen35° y sen r = sen15°

Poniendo los valores respectivos de los ángulos dados de la tabla de registro obtenemos

$\therefore \frac{sin\ 35^{\degree}} {sin\ 15^{\degree}}$ = 2,19

Por lo tanto, la constante para los valores anteriores es 2,19.

Pregunta 2: ¿Cuál es el valor del seno del ángulo de incidencia si el ángulo de refracción es de 35°? Se supone que la constante es 1,57.

Solución:

Como la conocemos,

$\frac{sin\ i}{sin\ r}$ = constante

La constante dada tiene valor = 1.57 y sen r =35° = 0.57

Poniendo los valores respectivos de los ángulos de la tabla de registro obtenemos

$\therefore \frac{sin\ i} {sin\ 35^{\degree}}= 1.57$

sen i = 1,57 × 0,57

{sen i} = 0,894

Por tanto, sen del ángulo de incidencia o sen i = 0,894.

Pregunta 3: ¿Cuál es el valor constante si el ángulo de incidencia es de 45° y el ángulo de refracción es de 60°?

Solución:

Como la conocemos,

$\frac{sin\ i}{sin\ r}$ = constante

Dado sen i = sen 45° y sen r = sen 60°

Poniendo los valores respectivos de los ángulos dados de la tabla de registro obtenemos

$\therefore \frac{sin\ 45^{\degree}} {sin\ 60^{\degree}} = 0.82$

Por lo tanto, se encuentra que el valor de la constante es 0.82.

Pregunta 4: ¿Qué le sucederá al rayo emergente que provendrá de la superficie de la losa de vidrio si el ángulo de incidencia es perpendicular oa lo largo del rayo normal?

Responder:

El emergente estará a lo largo de la propia normal, ya que el rayo incidente no sufrirá ninguna refracción cuando incida a lo largo del rayo normal en la superficie de la losa de vidrio.

Pregunta 5: ¿El rayo de luz que viaja desde la superficie de la losa de vidrio sufre alguna dispersión o desviación?

Responder:

No, el rayo de luz que viaja a través de la losa de vidrio no se enfrenta a ninguna dispersión ni a ninguna desviación, ya que las superficies de la losa de vidrio son iguales y opuestas entre sí, por lo que no se produce ningún fenómeno de desviación o dispersión.

Pregunta 6: Aplicando la fórmula del desplazamiento lateral, encuentre el desplazamiento lateral a través de una losa de vidrio que tiene un espesor de 5 cm y el ángulo de incidencia es de 45° y la refracción es de 30 ° .

Solución:

De la fórmula dada de desplazamiento lateral tenemos,

$l = t \frac{sin\ (i-r)} {cos\ r}$

Dado t = 5 cm, ∠i = 45° y ∠r = 30°

Por lo tanto, poniendo los valores en la ecuación anterior tenemos,

$\therefore l = 5 cm\frac{sin (45° - 30°)} {cos30°}$

$\therefore l = 5 cm \frac{sin (15°)} {cos30°}$

Poniendo los valores de ángulo respectivos de la tabla de registro obtenemos,

$\therefore l = 5 cm \frac{ 0.25 } {0.86 }$

$\therefore l = 5 cm \times 0.29$

largo = 1,45 cm

Por tanto, el desplazamiento o desplazamiento lateral es de 1,45 cm.

Pregunta 7: Aplicando la fórmula del desplazamiento lateral, encuentre el desplazamiento lateral a través de una losa de vidrio que tiene un espesor de 10 cm y el ángulo de incidencia es de 60 ° y la refracción es de 45 °.

Solución:

De la fórmula dada de desplazamiento lateral tenemos,

$l = t \frac{sin(i-r)} {cosr}$

Dado t = 10 cm, ∠i = 60° y ∠r = 45°

Por lo tanto, poniendo los valores en la ecuación anterior tenemos,

$\therefore l = 10 cm \frac{sin (60° - 45°)} {cos45°}$

$\therefore l = 10cm \frac{sin 15°} {cos 45°}$

Poniendo los valores de ángulo respectivos de la tabla de registro obtenemos,

$\therefore l = 10cm \frac{ 0.25 } { 0.70}$

$\therefore l = 10 cm \times 0.35$

largo = 3,5 cm

Por tanto, el corrimiento o desplazamiento lateral es de 3,5 cm.

Pregunta 8: Aplicando la fórmula de desplazamiento lateral, encuentre el espesor de una losa de vidrio dada que tiene un desplazamiento o desplazamiento lateral de 5 cm y el ángulo de incidencia es de 45° y la refracción es de 30 ° .

Solución:

De la fórmula del desplazamiento lateral tenemos,

$l = t \frac{sin(i-r)} {cosr}$

Dado l = 5 cm ∠i = 45° y ∠r = 30°

Por lo tanto, poniendo los valores en la ecuación anterior tenemos,

$\therefore 5 cm = t \frac{sin (45{{\degree}} - 30{{\degree}})} {cos30{{\degree}}}$

$\therefore 5 cm = t \frac{sin 15{{\degree}}} {cos30{{\degree}}}$

Poniendo los valores de ángulo respectivos de la tabla de registro obtenemos,

$\therefore 5 cm = t \frac{ 0.25 } {0.86 }$

$\therefore 5 cm = t \times 0.29$

$\therefore t = \frac{5cm}{0.29}$

Por lo tanto, el espesor de la losa dada es de 17,24 cm.