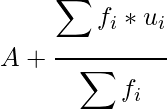Pregunta 1: El número de llamadas telefónicas recibidas en una central por intervalo durante 250 intervalos sucesivos de un minuto se dan en la siguiente tabla de frecuencias:
|
Número de llamadas |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
Número de intervalos |
15 |
24 |
29 |
46 |
54 |
43 |
39 |
Calcule el número medio de llamadas por intervalo.
Solución:
Deje que la media supuesta (A) sea = 3 (generalmente elegimos el elemento medio como la media supuesta, pero no es obligatorio),
por lo tanto, la tabla es,
Número de llamadas Número de intervalos
0
15
-3
-45
1
24
-2
-48
2
29
-1
-29
3
46
0
0
4
54
1
54
5
43
2
86
6
39
3
117
por lo tanto, media de las llamadas =
=
=
Por lo tanto, el número medio de llamadas por intervalo es 3,54
Pregunta 2: Se lanzaron cinco monedas simultáneamente 1000 veces, y en cada lanzamiento se observó el número de caras. El número de lanzamientos durante los cuales se obtuvieron 0, 1, 2, 3, 4 y 5 caras se muestra en la siguiente tabla. Encuentre el número medio de caras por lanzamiento.
|
Número de cabezas por lanzamiento |
0 |
1 |
2 |
3 |
4 |
5 |
|
Número de lanzamientos |
38 |
144 |
342 |
287 |
164 |
25 |
Solución:
Sea la media supuesta (A) = 2
por lo tanto, la tabla es,
Número de cabezas por lanzamiento
Número de lanzamientos
0
38
-2
-76
1
144
-1
-144
2
342
0
0
3
287
1
287
4
164
2
328
5
25
3
75
Número medio de cabezas por lanzamiento =
=
= 2,47
Por lo tanto, el número medio de caras por lanzamiento es 2,47
Pregunta 3: La siguiente tabla da el número de ramas y el número de plantas en el jardín de una escuela.
|
Numero de sucursales |
2 |
3 |
4 |
5 |
6 |
|
Número de plantas |
49 |
43 |
57 |
38 |
13 |
Calcular el número medio de ramas por planta.
Solución:
Sea la media supuesta (A) = 4
por lo tanto, la tabla es,
Numero de sucursales
Número de plantas
2
49
-2
-98
3
43
-1
-43
4
57
0
0
5
38
1
38
6
13
2
26
Promedio Número de sucursales por planta =
=
= 3.615
Por tanto, el número medio de ramas por planta es de 3.615
Pregunta 4: La siguiente tabla da el número de niños de 150 familias en un pueblo
|
Numero de niños |
0 |
1 |
2 |
3 |
4 |
5 |
|
Número de familias |
10 |
21 |
55 |
42 |
15 |
7 |
Encuentre el número promedio de hijos por familia.
Solución:
Sea la media supuesta (A) = 2
Por lo tanto, la tabla es,
Numero de niños
Número de familias
0
10
-2
-20
1
21
-1
-21
2
55
0
0
3
42
1
42
4
15
2
30
5
7
3
21
Promedio de hijos por familia =
=
= 2,35 (aproximadamente)
Por tanto, la media de hijos por familia es de 2,35 (aproximadamente)
Pregunta 5: Las notas obtenidas sobre 50, por 102 alumnos en una prueba de Física se dan en la siguiente tabla de frecuencias:
|
Marcas |
15 |
20 |
22 |
24 |
25 |
30 |
33 |
38 |
45 |
|
Frecuencia |
5 |
8 |
11 |
20 |
23 |
18 |
13 |
3 |
1 |
Encuentre el número promedio de puntos.
Solución:
Sea la media supuesta (A) = 25
por lo tanto, la tabla es,
Marcas
Frecuencia
15
5
-10
-50
20
8
-5
-40
22
11
-3
-33
24
20
-1
-20
25
23
0
0
30
18
5
90
33
13
8
104
38
3
13
39
45
1
20
20
Número medio de puntos =
=
= 26.08 (aproximadamente)
Por tanto, la media de puntos es de 26,08 (aproximadamente)
Pregunta 6: El número de estudiantes ausentes en una clase se registró todos los días durante 120 días y la información se da a continuación
|
Número de estudiantes ausentes |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Número de días |
1 |
4 |
10 |
50 |
34 |
15 |
4 |
2 |
Encuentre el número medio de estudiantes ausentes por día.
Solución:
Sea media supuesta media (A) = 3
Número de estudiantes ausentes
Número de días
0
1
-3
-3
1
4
-2
-8
2
10
-1
-10
3
50
0
0
4
34
1
34
5
15
2
30
6
4
3
12
7
2
4
8
Número medio de estudiantes ausentes por día =
=
= 3.525
Por lo tanto, la media de alumnos ausentes por día es de 3.525
Pregunta 7: En la primera prueba de lectura de un libro de 300 páginas se obtuvo la siguiente distribución de errores tipográficos:
|
Número de errores de imprenta por página |
0 |
1 |
2 |
3 |
4 |
5 |
|
Número de página |
154 |
95 |
36 |
9 |
5 |
1 |
Encuentre el número promedio de errores de imprenta por página.
Solución:
Sea la media supuesta (A) = 2
Número de errores de imprenta por página
Número de página
0
154
-2
-308
1
95
-1
-95
2
36
0
0
3
9
1
9
4
5
2
10
5
1
3
3
Promedio de errores de imprenta por día =
=
= 0,73
Por lo tanto, el promedio de errores de imprenta por día es de 0,73
Pregunta 8: Encuentre la media de la siguiente distribución de frecuencia de calificaciones en una prueba de estadística:
|
Número de accidentes |
0 |
1 |
2 |
3 |
4 |
|
Numero de trabajadores |
70 |
52 |
34 |
3 |
1 |
Encuentre el número promedio de errores de imprenta por página.
Solución:
Sea la media supuesta (A) = 2
Número de accidentes
Numero de trabajadores
0
70
-2
-140
1
52
-1
-52
2
34
0
0
3
3
1
3
4
1
2
2
Nº medio de accidentes por jornada trabajadores =
=
= 0,83
Por tanto, nº medio de accidentes por jornada trabajadores 0,83
Pregunta 9: Encuentre la media de la siguiente distribución de frecuencia de calificaciones en una prueba de estadística:
|
Marcas |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
|
Numero de estudiantes |
15 |
50 |
80 |
76 |
72 |
45 |
39 |
9 |
8 |
6 |
Solución:
Sea la media supuesta (A) = 25
Marcas
Numero de estudiantes
5
15
-20
-300
10
50
-15
-750
15
80
-10
-800
20
76
-5
-380
25
72
0
0
30
45
5
225
35
39
10
390
40
9
15
135
45
8
20
160
50
6
25
150
Media =
=
= 22.075
Por lo tanto, la media es 22.075
Publicación traducida automáticamente
Artículo escrito por jazymatricx y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA