Programa para comprobar la semejanza de dos triángulos dados

Dados cuatro arreglos de 3 números cada uno que representan lados y ángulos de dos triángulos. La tarea es verificar si dos triángulos son similares o no. Si es similar, imprime el teorema por el cual lo es.
Ejemplos:

Input : side1 = [2, 3, 3] angle1 = [80, 60, 40]
        side2 = [4, 6, 6]  angle2 = [40, 60, 80]
Output: Triangles are similar by SSS AAA SAS 

Input : side1 = [2, 3, 4] angle1 = [85, 45, 50]
        side2 = [4, 6, 6]  angle2 = [40, 60, 80]
Output: Triangles are not similar

Los triángulos semejantes son dos o más triángulos que tienen todos los ángulos correspondientes iguales y todos los lados correspondientes proporcionados. No importa en qué dirección estén mirando los triángulos. Su tamaño no importa siempre que cada lado sea proporcionado. La semejanza de los triángulos se puede demostrar mediante los siguientes teoremas:

Criterio de similitud Lado-Lado-Lado (SSS):
Si todos los lados de un triángulo son proporcionales a los lados correspondientes de otro triángulo, se dice que los triángulos son similares por la propiedad de Lado-Lado-Lado (SSS).
En un triángulo ABC y PQR si, los triángulos AB/PQ = BC/QR = CA/RP son semejantes.

Criterio de similitud Lado-Ángulo-Lado (SAS):
si dos lados de los dos triángulos son proporcionales y el ángulo entre ellos es el mismo en ambos triángulos, se dice que los triángulos son similares por la propiedad de Lado-Ángulo-Lado (SAS) .
En un triángulo ABC y PQR si, AB/PQ = BC/QR y $\measuredangle ABC$ = $\measuredangle PQR$ los triángulos son semejantes.

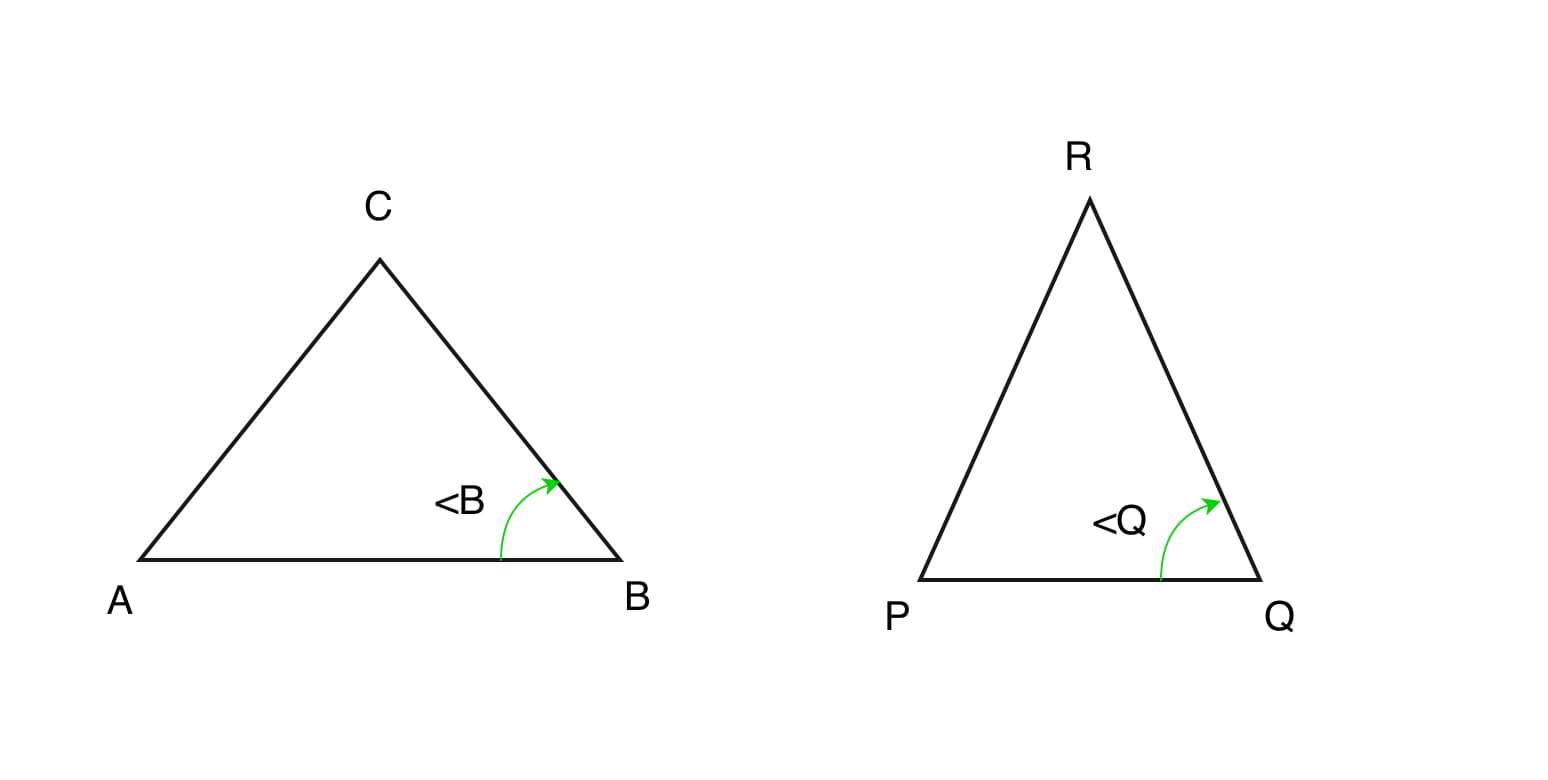
Criterio de similitud ángulo-ángulo-ángulo (AAA):
si todos los ángulos de un triángulo son iguales a los ángulos correspondientes de otro triángulo, se dice que los triángulos son similares por la propiedad de ángulo-ángulo-ángulo (AAA).
En un triángulo ABC y PQR si $\measuredangle ABC$ = $\measuredangle PQR$ , $\measuredangle BCA$ = $\measuredangle QRP$ y $\measuredangle CAB$ = $\measuredangle RPQ$ entonces los triángulos son semejantes.

A continuación se muestra la implementación del enfoque anterior:

C++

// C++ program to check
// similarity between
// two triangles.
#include<bits/stdc++.h>
using namespace std;
 
//Function for AAA similarity
int simi_aaa(int a1[], int a2[])
{
    sort(a1, a1 + 3);
    sort(a2, a2 + 3);
     
    // Check for AAA
    if (a1[0] == a2[0] &&
        a1[1] == a2[1] &&
        a1[2] == a2[2])
    return 1;
    else
    return 0;
     
}
 
// Function for
// SAS similarity
int simi_sas(int s1[], int s2[],
             int a1[], int a2[])
{
    sort(a1, a1 + 3);
    sort(a2, a2 + 3);
    sort(s1, s1 + 3);
    sort(s2, s2 + 3);
     
    // Check for SAS
     
    // angle b / w two smallest
    // sides is largest.
    if( s1[0] / s2[0] == s1[1] /
                         s2[1])
    {
        // since we take angle
        // b / w the sides.
        if (a1[2] == a2[2])        
            return 1;
    }
    if (s1[1] / s2[1] == s1[2] /
                         s2[2])
    {
        if (a1[0] == a2[0])
            return 1;
        }
    if (s1[2] / s2[2] == s1[0] /   
                         s2[0])
    {
        if(a1[1] == a2[1])
            return 1;
        }
    return 0;
}
 
// Function for SSS similarity
int simi_sss(int s1[], int s2[])
{
    sort(s1, s1 + 3);
    sort(s2, s2 + 3);
     
    // Check for SSS
    if(s1[0] / s2[0] == s1[1] / s2[1] &&
       s1[1] / s2[1] == s1[2] / s2[2] &&
       s1[2] / s2[2] == s1[0] / s2[0])
        return 1;
     
    return 0;
}
 
// Driver Code
int main()
{
    int s1[] = {2, 3, 3};
    int s2[] = {4, 6, 6};
         
    int a1[] = {80, 60, 40};
    int a2[] = {40, 60, 80};
 
    // function call for
    // AAA similarity
    int aaa = simi_aaa(a1, a2);
 
    // function call for
    // SSS similarity
    int sss = simi_sss(s1, s2) ;
 
    // function call for
    // SAS similarity
    int sas = simi_sas(s1, s2,
                       a1, a2) ;
 
    // Check if triangles
    // are similar or not
    if(aaa == 1 ||
       sss == 1 || sas == 1)
    {
        cout << "Triangles are "
             << "similar by ";
        if(aaa == 1) cout << "AAA ";
        if(sss == 1) cout << "SSS ";
        if(sas == 1) cout << "SAS.";
    }
     
    else
        cout << "Triangles are "
             << "not similar";
    return 0;
}
 
// This code is contributed
// by Arnab Kundu

Java

// Java program to check
// similarity between
// two triangles.
import java.util.*;
class GFG1
{
     
// Function for
// AAA similarity
static int simi_aaa(int a1[],
                    int a2[])
{
    Arrays.sort(a1);
    Arrays.sort(a2);
     
    // Check for AAA
    if (a1[0] == a2[0] &&
        a1[1] == a2[1] &&
        a1[2] == a2[2])
    return 1;
    else
    return 0;
     
}
 
// Function for
// SAS similarity
static int simi_sas(int s1[], int s2[],
                    int a1[], int a2[])
{
    Arrays.sort(a1);
    Arrays.sort(a2);
    Arrays.sort(s1);
    Arrays.sort(s2);
     
    // Check for SAS
     
    // angle b / w two smallest
    // sides is largest.
    if(s1[0] / s2[0] == s1[1] / s2[1])
    {
        // since we take angle
        // b / w the sides.
        if (a1[2] == a2[2])        
            return 1;
    }
    if (s1[1] / s2[1] == s1[2] / s2[2])
    {
        if (a1[0] == a2[0])
            return 1;
    }
    if (s1[2] / s2[2] == s1[0] / s2[0])
    {
        if(a1[1] == a2[1])
            return 1;
    }
    return 0;
}
 
// Function for
// SSS similarity
static int simi_sss(int s1[],
                    int s2[])
{
    Arrays.sort(s1);
    Arrays.sort(s2);
     
    // Check for SSS
    if(s1[0] / s2[0] == s1[1] / s2[1] &&
       s1[1] / s2[1] == s1[2] / s2[2] &&
       s1[2] / s2[2] == s1[0] / s2[0])
        return 1;
     
    return 0;
}
 
// Driver Code
public static void main(String args[])
{
    int s1[] = {2, 3, 3};
    int s2[] = {4, 6, 6};
         
    int a1[] = {80, 60, 40};
    int a2[] = {40, 60, 80};
 
    // function call for
    // AAA similarity
    int aaa = simi_aaa(a1, a2);
 
    // function call for
    // SSS similarity
    int sss = simi_sss(s1, s2) ;
 
    // function call for
    // SAS similarity
    int sas = simi_sas(s1, s2,
                       a1, a2) ;
 
    // Check if triangles
    // are similar or not
    if(aaa == 1 ||
       sss == 1 || sas == 1)
    {
        System.out.print("Triangles are " +
                         "similar by ");
        if(aaa == 1) System.out.print("AAA ");
        if(sss == 1) System.out.print("SSS ");
        if(sas == 1) System.out.print("SAS.");
    }
    else
        System.out.println("Triangles are " +
                           "not similar");
}
}
 
// This code is contributed
// by Arnab Kundu

Python

# Python program to check
# similarity between two triangles.
 
# Function for AAA similarity
def simi_aaa(a1, a2):            
    a1 = [float(i) for i in a1]
    a2 = [float(i) for i in a2]
    a1.sort()
    a2.sort()
     
    # Check for AAA
    if a1[0] == a2[0] and a1[1] == a2[1] and a1[2] == a2[2]:
        return 1
    return 0
 
# Function for SAS similarity
def simi_sas(s1, s2, a1, a2):
     
    s1 = [float(i) for i in s1]
    s2 = [float(i) for i in s2]
    a1 = [float(i) for i in a1]
    a2 = [float(i) for i in a2]
     
    s1.sort()
    s2.sort()
    a1.sort()
    a2.sort()
     
    # Check for SAS
     
    # angle b / w two smallest sides is largest.
    if s1[0] / s2[0] == s1[1] / s2[1]:
         
        # since we take angle b / w the sides.
        if a1[2] == a2[2]:        
            return 1
             
    if s1[1] / s2[1] == s1[2] / s2[2]:
        if a1[0] == a2[0]:
            return 1
             
    if s1[2] / s2[2] == s1[0] / s2[0]:
        if a1[1] == a2[1]:
            return 1
     
    return 0
 
# Function for SSS similarity
def simi_sss(s1, s2):
     
    s1 = [float(i) for i in s1]
    s2 = [float(i) for i in s2]
    s1.sort()
    s2.sort()
     
    # Check for SSS
    if(s1[0] / s2[0] == s1[1] / s2[1]
        and s1[1] / s2[1] == s1[2] / s2[2]
        and s1[2] / s2[2] == s1[0] / s2[0]):
        return 1
     
    return 0
     
 
# Driver Code
s1 = [2, 3, 3]
s2 = [4, 6, 6]
         
a1 = [80, 60, 40]
a2 = [40, 60, 80]
 
# function call for AAA similarity
aaa = simi_aaa(a1, a2)
 
# function call for SSS similarity
sss = simi_sss(s1, s2)
 
# function call for SAS similarity
sas = simi_sas(s1, s2, a1, a2)
 
# Check if triangles are similar or not
if aaa or sss or sas:
    print "Triangles are similar by",
    if aaa: print "AAA",
    if sss: print "SSS",
    if sas: print "SAS"
else: print "Triangles are not similar"

C#

// C# program to check
// similarity between
// two triangles.
 
using System;
 
class GFG1
{
     
// Function for
// AAA similarity
static int simi_aaa(int [] a1,
                    int [] a2)
{
    Array.Sort(a1);
    Array.Sort(a2);
     
    // Check for AAA
    if (a1[0] == a2[0] &&
        a1[1] == a2[1] &&
        a1[2] == a2[2])
    return 1;
    else
    return 0;
     
}
 
// Function for
// SAS similarity
static int simi_sas(int [] s1, int [] s2,
                    int [] a1, int [] a2)
{
    Array.Sort(a1);
    Array.Sort(a2);
    Array.Sort(s1);
    Array.Sort(s2);
     
    // Check for SAS
     
    // angle b / w two smallest
    // sides is largest.
    if(s1[0] / s2[0] == s1[1] / s2[1])
    {
        // since we take angle
        // b / w the sides.
        if (a1[2] == a2[2])        
            return 1;
    }
    if (s1[1] / s2[1] == s1[2] / s2[2])
    {
        if (a1[0] == a2[0])
            return 1;
    }
    if (s1[2] / s2[2] == s1[0] / s2[0])
    {
        if(a1[1] == a2[1])
            return 1;
    }
    return 0;
}
 
// Function for
// SSS similarity
static int simi_sss(int [] s1,
                    int [] s2)
{
    Array.Sort(s1);
    Array.Sort(s2);
     
    // Check for SSS
    if(s1[0] / s2[0] == s1[1] / s2[1] &&
    s1[1] / s2[1] == s1[2] / s2[2] &&
    s1[2] / s2[2] == s1[0] / s2[0])
        return 1;
     
    return 0;
}
 
// Driver Code
public static void Main()
{
    int [] s1 = {2, 3, 3};
    int [] s2 = {4, 6, 6};
         
    int [] a1 = {80, 60, 40};
    int [] a2 = {40, 60, 80};
 
    // function call for
    // AAA similarity
    int aaa = simi_aaa(a1, a2);
 
    // function call for
    // SSS similarity
    int sss = simi_sss(s1, s2) ;
 
    // function call for
    // SAS similarity
    int sas = simi_sas(s1, s2,
                    a1, a2) ;
 
    // Check if triangles
    // are similar or not
    if(aaa == 1 ||
    sss == 1 || sas == 1)
    {
        Console.Write("Triangles are " +
                        "similar by ");
        if(aaa == 1) Console.Write("AAA ");
        if(sss == 1) Console.Write("SSS ");
        if(sas == 1) Console.Write("SAS.");
    }
    else
        Console.WriteLine("Triangles are " +
                        "not similar");
}
}
 
// This code is contributed
// by Ryuga

PHP

<?php
// PHP program to check similarity between
// two triangles.
 
// Function for AAA similarity
function simi_aaa($a1, $a2)
{
    sort($a1);
    sort($a2);
     
    // Check for AAA
    if ($a1[0] == $a2[0] && $a1[1] == $a2[1] &&
                            $a1[2] == $a2[2])
        return 1;
    else
        return 0;
     
}
 
// Function for SAS similarity
function simi_sas($s1, $s2, $a1, $a2)
{
    sort($a1);
    sort($a2);
    sort($s1);
    sort($s2);
     
    // Check for SAS
     
    // angle b / w two smallest
    // sides is largest.
    if( $s1[0] / $s2[0] == $s1[1] / $s2[1])
    {
        // since we take angle b / w the sides.
        if ($a1[2] == $a2[2])    
            return 1;
    }
    if ($s1[1] / $s2[1] == $s1[2] / $s2[2])
    {
        if ($a1[0] == $a2[0])
            return 1;
    }
    if ($s1[2] / $s2[2] == $s1[0] / $s2[0])
    {
        if($a1[1] == $a2[1])
            return 1;
    }
    return 0;
}
 
// Function for SSS similarity
function simi_sss($s1, $s2)
{
    sort($s1);
    sort($s2);
     
    // Check for SSS
    if($s1[0] / $s2[0] == $s1[1] / $s2[1] &&
       $s1[1] / $s2[1] == $s1[2] / $s2[2] &&
       $s1[2] / $s2[2] == $s1[0] / $s2[0])
        return 1;
     
    return 0;
}
 
// Driver Code
$s1 = array(2, 3, 3);
$s2 = array(4, 6, 6);
     
$a1 = array(80, 60, 40);
$a2 = array(40, 60, 80);
 
// function call for
// AAA similarity
$aaa = simi_aaa($a1, $a2);
 
// function call for
// SSS similarity
$sss = simi_sss($s1, $s2) ;
 
// function call for
// SAS similarity
$sas = simi_sas($s1, $s2,
                $a1, $a2) ;
 
// Check if triangles
// are similar or not
if($aaa == 1 || $sss == 1 || $sas == 1)
{
    echo "Triangles are similar by ";
    if($aaa == 1) echo "AAA ";
    if($sss == 1) echo "SSS ";
    if($sas == 1) echo "SAS.";
}
 
else
    echo "Triangles are not similar";
 
// This code is contributed
// by ajit.
?>

Javascript

<script>
    // Javascript program to check
    // similarity between
    // two triangles.
     
    // Function for
    // AAA similarity
    function simi_aaa(a1, a2)
    {
        a1.sort(function(a, b){return a - b});
        a2.sort(function(a, b){return a - b});
 
        // Check for AAA
        if (a1[0] == a2[0] &&
            a1[1] == a2[1] &&
            a1[2] == a2[2])
            return 1;
        else
            return 0;
 
    }
 
    // Function for
    // SAS similarity
    function simi_sas(s1, s2, a1, a2)
    {
        a1.sort(function(a, b){return a - b});
        a2.sort(function(a, b){return a - b});
        s1.sort(function(a, b){return a - b});
        s2.sort(function(a, b){return a - b});
 
        // Check for SAS
 
        // angle b / w two smallest
        // sides is largest.
        if(s1[0] / s2[0] == s1[1] / s2[1])
        {
            // since we take angle
            // b / w the sides.
            if (a1[2] == a2[2])        
                return 1;
        }
        if (s1[1] / s2[1] == s1[2] / s2[2])
        {
            if (a1[0] == a2[0])
                return 1;
        }
        if (s1[2] / s2[2] == s1[0] / s2[0])
        {
            if(a1[1] == a2[1])
                return 1;
        }
        return 0;
    }
 
    // Function for
    // SSS similarity
    function simi_sss(s1, s2)
    {
        s1.sort(function(a, b){return a - b});
        s2.sort(function(a, b){return a - b});
 
        // Check for SSS
        if(s1[0] / s2[0] == s1[1] / s2[1] &&
        s1[1] / s2[1] == s1[2] / s2[2] &&
        s1[2] / s2[2] == s1[0] / s2[0])
            return 1;
 
        return 0;
    }
     
    let s1 = [2, 3, 3];
    let s2 = [4, 6, 6];
           
    let a1 = [80, 60, 40];
    let a2 = [40, 60, 80];
   
    // function call for
    // AAA similarity
    let aaa = simi_aaa(a1, a2);
   
    // function call for
    // SSS similarity
    let sss = simi_sss(s1, s2) ;
   
    // function call for
    // SAS similarity
    let sas = simi_sas(s1, s2, a1, a2) ;
   
    // Check if triangles
    // are similar or not
    if(aaa == 1 || sss == 1 || sas == 1)
    {
        document.write("Triangles are " + "similar by ");
        if(aaa == 1) document.write("AAA ");
        if(sss == 1) document.write("SSS ");
        if(sas == 1) document.write("SAS.");
    }
    else
        document.write("Triangles are not similar");
 
// This code is contributed by rameshtravel07.
</script>

Producción:

Triangles are similar by AAA SSS SAS

Complejidad del tiempo: O(1) Como las arrays tienen solo 3 elementos, el tiempo total empleado puede tratarse como constante.
Espacio Auxiliar: O(1)

Publicación traducida automáticamente

Artículo escrito por Amber_Saxena y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

C++

Java

Python

C#

PHP

Javascript

Deja una respuesta Cancelar la respuesta