Número de funciones posibles

En los siguientes artículos, vamos a calcular el número de funciones posibles a partir de dos conjuntos dados del elemento.

Enunciado:
Supongamos que hay dos conjuntos ‘A’ y ‘B’ que contienen ‘n’ y ‘m’ número de elementos respectivamente, es decir, Conjuntos,

'A' = {1, 2, 3, 4, ............, n},
'B' = {1, 2, 3, 4, ............, m} 

Entonces, el número de funciones posibles será cuando las funciones se cuenten desde el conjunto ‘A’ a ‘B’ y cuando las funciones se cuenten desde el conjunto ‘B’ a ‘A’.

Explicación:
en el siguiente diagrama, como podemos ver, el conjunto ‘A’ contiene elementos ‘n’ y el conjunto ‘B’ contiene el elemento ‘m’. Cada elemento del conjunto ‘A’ hace ‘m’ el número de funciones con cada elemento del conjunto ‘B’ y, por lo tanto, el número total de funciones posibles es .

Ejemplos:

1. Si el conjunto ‘A’ contiene el elemento ‘3’ y el conjunto ‘B’ contiene ‘2’ elementos, entonces el número total de funciones posibles será .
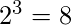2. Si el conjunto ‘A’ contiene el elemento ‘5’ y el conjunto ‘B’ contiene ‘2’ elementos, entonces el número total de funciones posibles será .

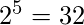Pero cuando las funciones se cuentan del conjunto ‘B’ a ‘A’, la fórmula será donde n, m son el número de elementos presentes en el conjunto ‘A’ y ‘B’ respectivamente, entonces los ejemplos serán los siguientes:

1. Si el conjunto ‘A’ contiene el elemento ‘3’ y el conjunto ‘B’ contiene ‘2’ elementos, entonces el número total de funciones posibles será .
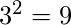2. Si el conjunto ‘A’ contiene el elemento ‘5’ y el conjunto ‘B’ contiene ‘2’ elementos, entonces el número total de funciones posibles será .

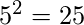De manera similar, cuando los dos conjuntos aumentan a 3 conjuntos,

'A' = {1, 2, 3, 4, ............, n},   
'B' = {1, 2, 3, 4, ............, m} 
'C' = {1, 2, 3, 4, ............, p}  

Entonces, el número de funciones posibles será cuando la función se cuente desde el Conjunto ‘A’ hasta el ‘B’, luego hasta el ‘C’ y así sucesivamente para cualquier número de conjuntos.