Mesa Cayley y grupo cíclico | Matemáticas

Mesa Cayley –

Si G es un grupo finito con la operación * , la tabla de Cayley de G es una tabla con filas y columnas etiquetadas por los elementos del grupo. La entrada en la fila etiquetada por y la columna etiquetada por es el elemento g*h.

Ejemplo: Construyamos la tabla de Cayley del grupo Z ₅ , los enteros {0, 1, 2, 3, 4} bajo suma mod 5.

Paso #1: Etiquetaremos las filas y columnas con los elementos de Z ₅ , en el mismo orden de izquierda a derecha y de arriba a abajo.
Paso #2: Completaremos la tabla. Cada entrada es el resultado de agregar la etiqueta de la fila a la etiqueta de la columna y luego reducir el módulo 5.

Características de la mesa Cayley –
• Cada fila y columna de la tabla debe contener cada elemento exactamente una vez. Si la tabla no tiene esta propiedad, no puede representar un grupo; la ley de cancelación no se sostiene.
• El elemento de identidad del grupo no solo debe aparecer en cada fila y columna (exactamente una vez), sino que también debe estar “distribuido simétricamente” alrededor de la diagonal principal. De lo contrario, uno o más elementos de la tabla no tienen inversa.
• No debe haber ninguna entrada en la tabla que no sea una etiqueta de fila/columna. En caso contrario, la operación no se cierra.
• Debe haber una fila en la que las etiquetas de las columnas aparezcan en orden, esto indica la presencia de un elemento de identidad. La columna de este elemento debe reflejar las etiquetas de las filas. De lo contrario, no hay identidad.

Nota: si la tabla de Cayley es simétrica a lo largo de su diagonal, entonces el grupo es un grupo abeliano.

grupo cíclico –

Es un grupo generado por un solo elemento, y ese elemento se llama generador de ese grupo cíclico. o un grupo cíclico G es aquel en el que cada elemento es una potencia de un elemento particular g, en el grupo. Es decir, cada elemento de G puede escribirse como g ⁿ para algún entero n para un grupo multiplicativo, o ng para algún entero n para un grupo aditivo. Entonces, g es un generador del grupo G.

Propiedades del Grupo Cíclico:
1. Todo grupo cíclico es también un grupo abeliano.
2. Si G es un grupo cíclico con generador g y orden n. Si m < n, entonces el orden del elemento g ^m viene dado por,
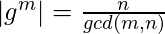
3. Todo subgrupo de un grupo cíclico es cíclico.
4. Si G es un grupo cíclico finito con orden n, el orden de cada elemento en G divide a n.
5. Si d es un divisor positivo de n, el número de elementos de orden d en un grupo cíclico de orden n es Φ(d), donde Φ(d) es la función Euler Phi .
6. El orden de un grupo cíclico y el orden de su generador es el mismo.

Preguntas GATE relacionadas:
1) Gate CS 2004
2) Gate CS 2009