Problema SAT : SAT (Boolean Satisfiability Problem) es el problema de determinar si existe una interpretación que satisfaga una fórmula booleana dada. Pregunta si las variables de una fórmula booleana determinada se pueden reemplazar consistentemente por los valores VERDADERO o FALSO de tal manera que la fórmula se evalúe como VERDADERO . Si este es el caso, la fórmula se llama satisfacible . Por otro lado, si no existe tal asignación, la función expresada por la fórmula es FALSA para todas las posibles asignaciones de variables y la fórmula es insatisfactoria .
Problema : dada una fórmula booleana f , el problema es identificar si la fórmula f tiene una asignación satisfactoria o no.
Explicación : una instancia del problema es una entrada especificada para el problema. Una instancia del problema es una fórmula booleana f . Dado que un problema NP-completo es un problema que es tanto NP como NP-Difícil , la prueba o afirmación de que un problema es NP-Completo consta de dos partes:
- El problema en sí está en la clase NP.
- Todos los demás problemas en la clase NP pueden ser reducibles en tiempo polinomial a eso.
(B es reducible en tiempo polinomial a C se denota como ≤ P C )
Si solo se cumple la segunda condición, el problema se llama NP-Hard .
Pero no es posible reducir cada problema NP en otro problema NP para mostrar su NP-Completo todo el tiempo, es decir, mostrar que un problema es NP-completo y luego probar que el problema está en NP y cualquier problema NP-Completo es reducible a es decir, si B es NP-Completo y B ≤ P C Para C en NP, entonces C es NP-Completo. Así, se puede verificar que el Problema SAT es NP-Completo usando las siguientes proposiciones:
SAT está en NP :
si algún problema está en NP, luego se le otorga un ‘certificado’, que es una solución al problema y una instancia del problema (una fórmula booleana f ) que podremos verificar (identificar si la solución es correcto o no) certificado en tiempo polinomial. Esto se puede hacer comprobando si la asignación dada de variables satisface la fórmula booleana.
SAT es NP-Hard :
para probar que este problema es NP-Hard, reduzca un problema conocido, Circuit-SAT en este caso a nuestro problema. El circuito booleano C se puede corregir en una fórmula booleana como:
- Para cada cable de entrada, agregue una nueva variable y i .
- Para cada cable de salida, agregue una nueva variable Z .
- Se prepara una ecuación para cada puerta.
- Estos conjuntos de ecuaciones están separados por
Esta transformación se puede hacer en tiempo lineal. Ahora se cumplen las siguientes proposiciones:
- Si hay un conjunto de valores variables de entrada que satisfacen el circuito, entonces puede derivar una asignación para la fórmula f que satisface la fórmula. Esto se puede simular calculando la salida de cada puerta en el circuito.
- Si hay una asignación satisfactoria para la fórmula f , esto puede satisfacer el circuito booleano después de la eliminación de las variables recién agregadas.
Por ejemplo: si debajo está el circuito, entonces: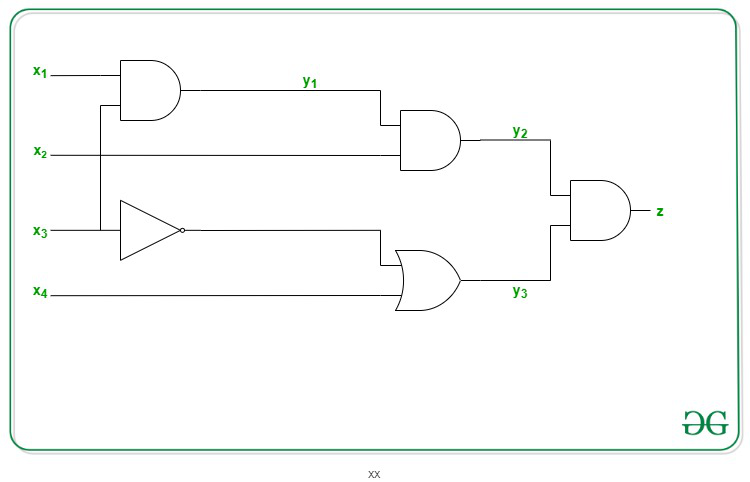
Por lo tanto, el Problema SAT es NP-Completo.
Publicación traducida automáticamente
Artículo escrito por yashchuahan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA