Noam Chomsky ha dividido la gramática en cuatro tipos :
|
Escribe |
Nombre |
|
0 |
Gramática sin restricciones |
|
1 |
Gramática sensible al contexto |
|
2 |
Gramática libre de contexto |
|
3 |
Gramática regular |
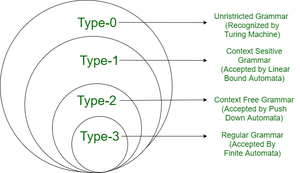
Jerarquía de Chomsky
1. Gramática libre de contexto:
- El lenguaje generado por Context Free Grammar es aceptado por Pushdown Automata
- Es un subconjunto de la gramática Tipo 0 y Tipo 1 y un superconjunto de la gramática Tipo 3.
- También llamada gramática estructurada en fases.
- Diferentes gramáticas libres de contexto pueden generar el mismo lenguaje libre de contexto.
- La clasificación de la gramática libre de contexto se realiza sobre la base del número de árboles de análisis.
- Solo un árbol de análisis-> Inequívoco.
- Más de un árbol de análisis->Ambiguo.
Las producciones están en la forma –
A->B; A∈N i.e A is a non-terminal. B∈V*(Any string).
Ejemplo –
S –> AB A –> a B –> b
2. Gramática regular:
- Es aceptado por Finite State Automata.
- Es un subconjunto de la gramática Tipo 0, Tipo 1 y Tipo 2.
- El lenguaje que genera se llama Lenguaje Regular.
- Los lenguajes regulares se cierran bajo operaciones como Unión, Intersección, Complemento, etc.
- Son la forma más restringida de gramática.
Las producciones están en la forma –
V –> VT / T (left-linear grammar) (or) V –> TV /T (right-linear grammar)
Ejemplo –
1. S –> ab. 2. S -> aS | bS | ∊
Diferencia entre la gramática libre de contexto y la gramática regular:
| Parámetro | Gramática libre de contexto | Gramática regular |
| Escribe | Tipo 2 | Tipo-3 |
| reconocedor | Autómatas de empuje hacia abajo. | Autómatas de estado finito |
| Normas | Las producciones son de la forma: A->B; A∈N(No terminal) B∈V * (Cualquier string) |
Las producciones son de la forma: V –> VT / T (gramática lineal a la izquierda) (o) V –> TV /T (gramática lineal a la derecha) |
| Restricción | Menos que la gramática regular | Más que cualquier otra gramática |
| Lado derecho | El lado derecho de la producción no tiene restricciones. | El lado derecho de la producción debe ser lineal a la izquierda o lineal a la derecha. |
| Establecer propiedad | Súper conjunto de gramática regular | Subconjunto de gramática libre de contexto |
| Intersección | La intersección de dos CFL no necesita ser una CFL | La intersección de dos RG es un RG. |
| Complementar | No son cerrados bajo complemento. | Cerrado bajo complemento |
| Rango | La gama de idiomas que se incluyen en CFG es amplia. | La variedad de idiomas que se incluyen en RG es menor que en CFG. |
| Ejemplos | S –> AB;A –> a;B –> b | S -> comoS | bS | ∊ |
Publicación traducida automáticamente
Artículo escrito por parthbanathia y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA