LATEX es un sistema de preparación de documentos para producir documentos de apariencia profesional. LaTeX se usa ampliamente para la comunicación y publicación de documentos científicos en muchos campos, incluidas las matemáticas, la estadística, la informática, la ingeniería, la física, etc. También tiene un papel destacado en la preparación y publicación de libros y artículos que contienen materiales multilingües complejos. , como el sánscrito y el griego.
Entonces, en esta publicación, hemos discutido los comandos TEX más utilizados para matemáticas.
- Fracciones:
en lugar de escribir fracciones como A / B, usaremos la siguiente
sintaxis Sintaxis:\frac{numerator}{denominator}Ejemplo –
\frac{a+1}{b+1}PRODUCCIÓN:
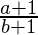
- N-ésima potencia:
en lugar de escribir potencias como x ^ n, lo que no está claro como si fuera xor o potencia, por lo que usaremos la siguiente sintaxis Sintaxis
:x^y
Ejemplo –
x^2
PRODUCCIÓN:
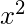
- Raíz enésima:
En lugar de escribir raíces como x^(1/N), lo cual no está claro como si fuera xor o raíz, por lo que usaremos la siguiente sintaxis Sintaxis
:\sqrt[N]{27}Ejemplo –
\sqrt[3]{27}PRODUCCIÓN:
![Rendered by QuickLaTeX.com \sqrt[3]{27}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-dc99d3599ed0ae91dd93e49687b93aee_l3.png)
- Arrays
En lugar de escribir arrays como [[1, x, x^2], [1, y, y^2][1, z, z^2]], que no es muy claro, use la siguiente sintaxis Sintaxis
:\begin{matrix} 1 & x & x^2 \\ 1 & y & y^2 \\ 1 & z & z^2 \\ \end{matrix}Ejemplo –
\begin{matrix} 1 & x & x^2 \\ 1 & y & y^2 \\ 1 & z & z^2 \\ \end{matrix}PRODUCCIÓN:
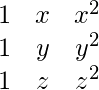
- Definiciones por casos (función por partes) es una función definida por múltiples subfunciones, cada subfunción se aplica a un cierto intervalo del dominio de la función principal, un subdominio.
Sintaxis:
f(n) = \begin{cases} n/2, & \text{if $n$is even} \\ n+1, & \text{if $n$is odd} \end{cases}Ejemplo –
f(n) = \begin{cases} n/2, & \text{if $n$is even} \\ n+1, & \text{if $n$is odd} \end{cases}PRODUCCIÓN:
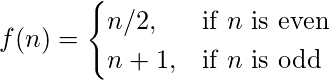
- El sistema de ecuaciones es una función definida por múltiples subfunciones, cada subfunción se aplica a un determinado intervalo del dominio de la función principal, un subdominio.
Sintaxis:
\left\{ \begin{array}{c} a_1x+b_1y+c_1z=d_1 \\ a_2x+b_2y+c_2z=d_2 \\ a_3x+b_3y+c_3z=d_3 \end{array} \right.Ejemplo –
\left\{ \begin{array}{c} a_1x+b_1y+c_1z=d_1 \\ a_2x+b_2y+c_2z=d_2 \\ a_3x+b_3y+c_3z=d_3 \end{array} \right.PRODUCCIÓN:

- La sumatoria es la suma de una secuencia de cualquier tipo de números, llamados sumandos o sumandos; el resultado es su suma o total.
Sintaxis:
\sum_{i=0}^n i^2Ejemplo –
\sum_{i=0}^n i^2PRODUCCIÓN:
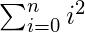
- subíndices es un carácter que se establece ligeramente por debajo de la línea normal de tipo.
Sintaxis:
\log_2 x
Ejemplo –
\log_2 x
PRODUCCIÓN:
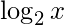
- floor es la función que toma como entrada un número real y da como salida el mayor entero menor o igual que, denotado.
Sintaxis:
\lfloor n \rfloor
Ejemplo –
\lfloor 2.2 \rfloor
PRODUCCIÓN:
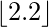
- La función ceil se asigna al menor entero mayor o igual que, denotado.
Sintaxis:
\lceil n \rcei
Ejemplo –
\lceil 2.5 \rceil
PRODUCCIÓN:
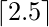
- Algunos ejemplos combinados:
- Ejemplo –
- Usar
\sum_{i=0}^n i^2 = \frac{(n^2+n)(2n+1)}{6}por
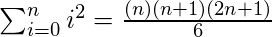
- Usar
\left(\frac{\sqrt x}{y^3}\right)por
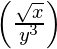
- Usar
\Biggl(\biggl(\Bigl(\bigl((n)\bigr)\Bigr)\biggr)\Biggr)
por
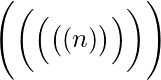
- Usar
\sqrt[3]{\frac xy}por
![Rendered by QuickLaTeX.com \sqrt[3]{\frac xy}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3052e669790f13a6d917962af892ce11_l3.png)
Ejemplo –
Ejemplo –
Ejemplo –
- Usar