Permutaciones pares:
Una permutación se llama incluso si se puede expresar como un producto de un número par de transposiciones.
Ejemplo 1:
![]()
![]()
![]()
Aquí podemos ver que la permutación ( 1 2 3 ) se ha expresado como producto de transposiciones de tres maneras y en cada una de ellas el número de transposiciones es par, por lo que es una permutación par.
Ejemplo-2:
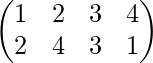
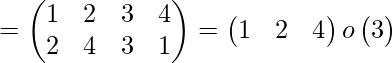
![]()
La permutación dada es el producto de dos transposiciones, por lo que es una permutación uniforme.
Permutaciones impares:
Una permutación se llama impar si se puede expresar como un producto de un número impar de transposiciones.
Ejemplo 1:
![]()
![]()
![]()
Aquí podemos ver que la permutación ( 3 4 5 6 ) se ha expresado como producto de transposiciones de dos formas y en cada una de ellas el número de transposiciones es impar, por lo que es una permutación impar.
Ejemplo-2:
![]()
![]()
La permutación dada es el producto de cinco transpuestas, por lo que es una permutación impar.
Teoremas sobre permutaciones pares e impares:
Teorema-1:
Si P1 y P2 son permutaciones, entonces
- (a) P1 P2 es par siempre que P1 y P2 sean pares o impares.
- (b) P1 P2 es impar siempre que uno de P1 y P2 sea impar y el otro par.
Prueba: (a)
Caso I. Si P1, P2 ambos son pares.
Sean P1 y P2 el producto de las transposiciones 2n y 2m respectivamente, donde n y m son números enteros positivos.
Entonces, cada uno de P1 P2 y P2 P1 es producto de transposiciones de 2n + 2m, donde 2n + 2m es evidentemente un número entero par.
Por lo tanto, P1 P2 y P2 P1 son permutaciones pares.
Caso II . Si P1, P2, ambos son impares. Sea P1 P2 el producto de las transposiciones (2n + 1) y (2m + 1) respectivamente, donde n y m son números enteros positivos.
Entonces cada uno de P1 P2 y P2 P1 es el producto (2n + 1) + (2m + 1) es decir, 2 (n + m + 1) transposiciones, donde 2(n + m + 1) es evidentemente un número entero par.
Por lo tanto, P1 P2 y P2 P1 son permutaciones pares.
Prueba: (b)
Sea P1 una permutación impar y P2 una permutación par. También sean P1 y P2 el producto de las transposiciones (2n + 1) y 2m respectivamente, donde n y m son números enteros positivos.
Entonces, cada uno de P1 P2 y P2 P1 es el producto de (2n + 1) + 2m, es decir, [2 (n+ m)+1] transposiciones, donde 2(n+ m) + 1 es evidentemente un número entero impar.
Por lo tanto, P1 P2 y P2 P1 son permutaciones impares.
Teorema-2:
La permutación de Identidad es una permutación par.
Prueba-: La permutación de identidad l siempre se puede expresar como el producto de dos transposiciones (es decir, pares).
Por ejemplo
Por lo tanto, I es una permutación par. (Ver definición)
Teorema-3:
El inverso de una permutación par es una permutación par.
Prueba-: Si P es una permutación par y P -1 es su inversa, entonces PP -1 = I, la permutación identidad.
Pero P e I son pares (Ver Teorema 2 arriba),
entonces P -1 también es par (Ver Teorema 1 (a) arriba)
Teorema 4:
El inverso de una permutación impar es una permutación impar.
Prueba-: Si P es una permutación impar y P -1 es su inversa, entonces PP -1 = I, la permutación identidad.
Pero P es impar y I es par. (Véase el Teorema 2 anterior),
entonces P -1 también es impar. (Véase el Teorema 1 (b) anterior)
Publicación traducida automáticamente
Artículo escrito por portalpirate y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA