En este artículo, veremos algunas ideas muy básicas sobre el Análisis Real , es decir, el estudio de la estructura del Sistema de Números Reales. Discutiremos los tres axiomas que se consideran satisfechos por el conjunto de los Números Reales, ![]()
Los tres axiomas son:
- Axiomas de campo
- Axiomas de orden
- Axioma de completitud
Axiomas de campo : El conjunto ![]() se representa como un campo
se representa como un campo ![]() donde
donde ![]() y
y ![]() son las operaciones binarias de suma y multiplicación respectivamente. Consta de 4 axiomas de suma y multiplicación cada uno y una ley distributiva.
son las operaciones binarias de suma y multiplicación respectivamente. Consta de 4 axiomas de suma y multiplicación cada uno y una ley distributiva.
(i) Axiomas para la suma:
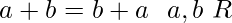
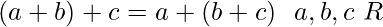
- R contiene un elemento 0 tal que
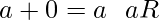
- A cada uno
 le corresponde un elemento
le corresponde un elemento 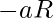 tal que
tal que 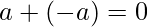
(ii) Axiomas para la multiplicación:
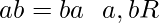
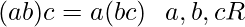
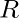 contiene un elemento
contiene un elemento 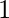 tal que
tal que 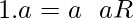 y
y 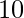
- Si
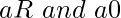 entonces existe un elemento
entonces existe un elemento 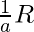 tal que
tal que 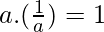
(iii) La ley distributiva:
Axiomas de orden : Definimos ![]() (Mayor que) como la relación de orden, y satisface los siguientes axiomas:
(Mayor que) como la relación de orden, y satisface los siguientes axiomas:
- Ley de la tricotomía:
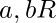 solo una de las expresiones puede ser verdadera:
solo una de las expresiones puede ser verdadera: 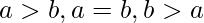
- Transitividad – Para
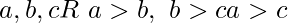
- Propiedad Monótona para la suma – Para
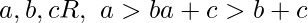
- Propiedad Monótona para la multiplicación – Para
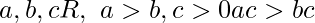
Lo llamamos ![]() orden lineal y
orden lineal y ![]() se le llama campo linealmente ordenado .
se le llama campo linealmente ordenado .
Antes de definir el Axioma de Completitud, veremos el concepto de Acotación. Aquí, definiremos algunos términos antes de establecer el Axioma de Completitud.
Agregado : cualquier subconjunto no vacío, por ejemplo ![]() , de
, de ![]() se conoce como agregado . Por ejemplo, el conjunto
se conoce como agregado . Por ejemplo, el conjunto ![]() es un agregado. De manera similar, el conjunto B = {1,2,4,8} también es un agregado ya que
es un agregado. De manera similar, el conjunto B = {1,2,4,8} también es un agregado ya que ![]() Pero, el conjunto A = {x,y,z} y el conjunto vacío
Pero, el conjunto A = {x,y,z} y el conjunto vacío ![]() no son agregados.
no son agregados.
Cota superior : Se dice que un subconjunto ![]() de
de ![]() está acotado por arriba si es
está acotado por arriba si es ![]() tal que
tal que ![]() . Este número
. Este número ![]() se llama límite superior de
se llama límite superior de ![]() . Por ejemplo, el conjunto
. Por ejemplo, el conjunto ![]() de números reales negativos está acotado por arriba y
de números reales negativos está acotado por arriba y ![]() es un límite superior. De manera similar, el conjunto
es un límite superior. De manera similar, el conjunto ![]() de enteros negativos está acotado por arriba y
de enteros negativos está acotado por arriba y ![]() es el límite superior. Pero, el conjunto
es el límite superior. Pero, el conjunto ![]() de números reales positivos no está acotado arriba.
de números reales positivos no está acotado arriba.
Límite inferior : se dice que un subconjunto ![]() de
de ![]() está acotado por debajo si
está acotado por debajo si ![]() este
este ![]() número
número ![]() se denomina límite inferior de S. Por ejemplo, el conjunto
se denomina límite inferior de S. Por ejemplo, el conjunto ![]() está acotado por debajo y
está acotado por debajo y ![]() es un límite inferior. De manera similar, el conjunto
es un límite inferior. De manera similar, el conjunto ![]() está acotado por abajo y
está acotado por abajo y ![]() es el límite superior. Pero, el conjunto
es el límite superior. Pero, el conjunto ![]() no está acotado por debajo.
no está acotado por debajo.
Least Upper Bound : considere un límite superior ![]() de un agregado
de un agregado ![]() y cualquier número real menor que
y cualquier número real menor que ![]() no sea un límite superior de
no sea un límite superior de ![]() , entonces decimos que
, entonces decimos que ![]() es el límite superior mínimo (lub) o supremum (sup) de
es el límite superior mínimo (lub) o supremum (sup) de ![]()
Límite inferior más grande : considere un límite inferior ![]() de un agregado
de un agregado ![]() y cualquier número real mayor que
y cualquier número real mayor que ![]() no sea un límite inferior de
no sea un límite inferior de ![]() , entonces decimos que
, entonces decimos que ![]() es el límite inferior más grande (glb) o infimum (inf) de
es el límite inferior más grande (glb) o infimum (inf) de ![]()
Ejemplo : Sea ![]() . Para S, vemos que 1 es un límite superior y cualquier número menor que 1 no es un límite superior de S, por lo tanto, 1 es supremo de S. Además, 0 es un límite inferior y cualquier número mayor que 0 no es un límite inferior. acotado, entonces, 0 es el mínimo de S.
. Para S, vemos que 1 es un límite superior y cualquier número menor que 1 no es un límite superior de S, por lo tanto, 1 es supremo de S. Además, 0 es un límite inferior y cualquier número mayor que 0 no es un límite inferior. acotado, entonces, 0 es el mínimo de S.
Acotación : un agregado S está acotado si está acotado por arriba y por abajo. Es decir, debe tener un límite superior y un límite inferior. Por ejemplo, cualquier conjunto finito está acotado, el conjunto vacío ![]() está acotado. Pero, los conjuntos
está acotado. Pero, los conjuntos ![]() y
y ![]() no están acotados.
no están acotados.
Nota : No es necesario que un agregado tenga un miembro mayor y uno menor para estar acotado por arriba o por abajo, respectivamente.
Ahora que hemos terminado con la definición requerida, establecemos el Axioma de Completitud (también llamado el axioma del límite superior mínimo) .
«Todo conjunto no vacío de números reales que está acotado arriba tiene un supremo».
El conjunto R satisface los axiomas de campo, los axiomas de orden y el axioma de completitud . Por lo tanto, el conjunto de números reales ![]() se llama un cuerpo ordenado completo.
se llama un cuerpo ordenado completo.
Además, el conjunto de los números racionales ![]() no satisface el axioma de completitud. Por lo tanto,
no satisface el axioma de completitud. Por lo tanto, ![]() no es un campo completo.
no es un campo completo.
El axioma de completitud es una propiedad realmente fundamental e importante de los sistemas de números reales, como pruebas de varios teoremas de cálculo, los conceptos de máximos y mínimos, teoremas de valor medio, etc., se basan en la propiedad de completitud de los números reales.
Publicación traducida automáticamente
Artículo escrito por shashanksamavedula1999 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA