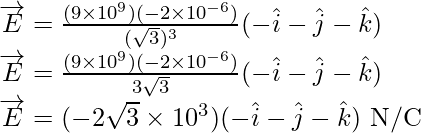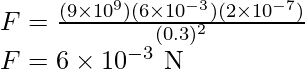Campo eléctrico debido a una carga puntual

La carga eléctrica es una propiedad fundamental de la materia que controla cómo un campo eléctrico o magnético afecta a las partículas elementales. La carga eléctrica existe en unidades naturales discretas que no pueden generarse ni destruirse. Las cargas positivas y negativas son los dos tipos de cargas eléctricas. Cuando dos elementos con un exceso de un tipo de carga están lo suficientemente cerca, se repelen entre sí. Cuando dos objetos con carga positiva y carga negativa están en estrecho contacto, se atraen entre sí.

Muchas partículas fundamentales o subatómicas de material comparten la propiedad de la carga eléctrica. Los protones tienen carga positiva, mientras que los electrones tienen carga negativa. Los neutrones, por otro lado, son partículas sin carga o neutras. La carga negativa de cada electrón y la carga positiva de cada protón tienen la misma magnitud, según los experimentos. La carga de un electrón o protón, que es una constante física fundamental, se mide en unidades naturales.

Campo eléctrico debido a una carga puntual

Considere una carga puntual Q en el origen O, que se coloca en el vacío. La ley de Coulomb establece que si se coloca otra carga puntual q en una posición P donde OP = r, la carga Q ejercerá una fuerza sobre q. La carga Q genera un campo eléctrico que se extiende por todo el entorno. Cuando se introduce una nueva carga, q, en el punto P, el campo actúa sobre ella y genera una fuerza. El campo eléctrico producido por una carga Q en una ubicación r se puede expresar como,

$E(r)=\frac{1}{4\pi\epsilon_0}\frac{Q}{r^2}\hat{r}$

donde r = r/r es un vector unitario desde el origen hasta el punto r. Como resultado, la expresión anterior especifica el valor del campo eléctrico para cada valor del vector de posición r. El término «campo» se refiere a cómo una cantidad distribuida (que podría ser un escalar o un vector) varía con la posición. La existencia del campo eléctrico se ha combinado con el efecto de la carga. La fuerza F ejercida por una carga Q sobre una carga q se calcula como

$F=\frac{1}{4\pi\epsilon_0}\frac{Qq}{r^2}\hat{r}$

Campo eléctrico (a) debido a una carga Q, (b) debido a una carga –Q.

Vale la pena señalar que la carga q tiene una fuerza igual y opuesta sobre la carga Q.

La fuerza electrostática entre las cargas Q y q puede verse como una interacción entre la carga q y el campo eléctrico de Q, y viceversa. La carga q siente una fuerza F igual a la carga q multiplicada por el campo eléctrico E en la ubicación de q si su posición está denotada por el vector r.

Por lo tanto,

F(r) = qE(r)

La unidad SI del campo eléctrico como N/C.

Aquí hay algunos puntos clave a considerar:

El campo eléctrico producido por una carga Q es numéricamente equivalente a la fuerza ejercida por ella si q es la unidad. Como resultado, el campo eléctrico producido por una carga Q en un lugar dado del espacio puede describirse como la fuerza que experimentaría una unidad de carga positiva si se colocara allí. La carga Q que genera el campo eléctrico se conoce como carga fuente, mientras que la carga q que mide el efecto de una carga fuente se conoce como carga de prueba. Es importante tener en cuenta que la fuente de carga Q debe permanecer en su lugar original. Sin embargo, si se aplica una carga q en cualquier lugar alrededor de Q, Q estará sujeto a una fuerza eléctrica como resultado de q y comenzará a moverse. Hacer que q sea insignificantemente pequeño es un enfoque para solucionar este problema. Por lo tanto, la fuerza F es despreciablemente pequeña, pero la relación F/q es finita,

$E=\lim_{q \rightarrow0}\left(\frac{F}{q}\right)$

Vale la pena señalar que el campo eléctrico E causado por Q es independiente de q, a pesar de que se describe operativamente en términos de alguna carga de prueba q. Esto se debe a que F es proporcional a q, por lo que la relación F/q es independiente de q. La fuerza F ejercida sobre la carga q por la carga Q está determinada por la ubicación específica de la carga q, que puede tener cualquier valor en la región que rodea la carga Q. Como resultado, el campo eléctrico E producido por Q también se ve afectado por la coordenada espacial r. Recibimos valores variados de campo eléctrico E para diferentes lugares de la carga q a través del espacio. Cada punto en el espacio tridimensional contiene el campo.
El campo eléctrico de una carga positiva se irradiará hacia el exterior. Si la carga de la fuente es negativa, por otro lado, el vector de campo eléctrico en cada punto apunta hacia adentro radialmente.
Debido a que la cantidad de fuerza F sobre la carga q debido a la carga Q está determinada únicamente por la distancia r de la carga q a la carga Q, la magnitud del campo eléctrico E también está determinada únicamente por la distancia r. Como resultado, el tamaño del campo eléctrico E de la carga Q es el mismo a distancias iguales de ella. En una esfera con la carga puntual en su centro, la magnitud del campo eléctrico E debido a una carga puntual es, por tanto, la misma; en otras palabras, posee simetría esférica.

Campo eléctrico debido a un sistema de cargas.

El campo eléctrico en un punto debido a un sistema de cargas es la suma vectorial de los campos eléctricos en el punto debido a cargas individuales.

Considere un sistema de cargas q ₁ , q ₂ ,…, qn con vectores de posición r ₁ , r ₂ ,…, r _n con respecto a algún origen O. La fuerza experimentada por una unidad de carga de prueba colocada en ese punto, sin alterar la posiciones originales de las cargas q ₁ , q ₂ ,…, q _n , se describe como el campo eléctrico en un punto del espacio debido a un sistema de cargas, similar al campo eléctrico en un punto del espacio debido a una sola carga. Para determinar este campo en una ubicación P representada por el vector de posición r, podemos aplicar la ley de Coulomb y el principio de superposición.

El campo eléctrico E ₁ en r debido a q ₁ en r ₁ se puede escribir como,

$E_1=\frac{1}{4\pi\epsilon_0}\frac{q_1}{r_{1P}^2}\hat{r}_{1P}$

donde $\hat{r}_{1P}$ es un vector unitario en la dirección de q ₁ a P, y r _1P es la distancia entre q ₁ y P.

De manera similar, el campo eléctrico E ₂ en r debido a q ₂ en r ₂ se puede expresar como,

$E_2=\frac{1}{4\pi\epsilon_0}\frac{q_2}{r_{2P}^2}\hat{r}_{2P}$

donde $\hat{r}_{2P}$ es un vector unitario en la dirección de q ₂ a P y r _2P es la distancia entre q ₂ y P. Expresiones similares para campos E ₃ , E ₄ , …, E _n debido a cargas q ₃ , q ₄ , …, q _norte _ Por el principio de superposición, el campo eléctrico E en r debido al sistema de cargas se puede expresar como,

$E(r) = E_1(r) + E_2(r) + … + E_n(r)\\ E(r)=\frac{1}{4\pi\epsilon_0}\frac{q_1}{r_{1P}^2}\hat{r}_{1P}+\frac{1}{4\pi\epsilon_0}\frac{q_2}{r_{2P}^2}\hat{r}_{2P}+ ... +\frac{1}{4\pi\epsilon_0}\frac{q_n}{r_{nP}^2}\hat{r}_{nP}\\ E(r)=\frac{1}{4\pi\epsilon_0}\sum_{i=1}^n\frac{q_i}{r_{iP}^2}\hat{r}_{iP}$

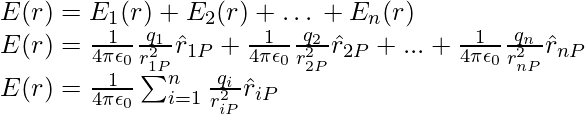
E es una variable vectorial que varía de una ubicación en el espacio a otra y está determinada por las posiciones de carga de la fuente.

Importancia física del campo eléctrico.

El concepto de campo eléctrico es útil en electrostática, pero no es absolutamente necesario. Un enfoque elegante para describir el entorno eléctrico de un sistema de cargas es utilizar el término campo eléctrico.

La fuerza que experimentaría una unidad de carga de prueba positiva si se colocara en una posición en el espacio alrededor de un sistema de cargas (sin trastornar el sistema) está determinada por el campo eléctrico en ese punto. El campo eléctrico es una propiedad del sistema de cargas y no está relacionado con la carga de prueba utilizada para calcular el campo. En física, un campo es una cantidad que se define en cada punto del espacio y puede variar de un punto a otro. Como la fuerza es una cantidad vectorial, el campo eléctrico es un campo vectorial.

Sin embargo, cuando vamos más allá de la electrostática y consideramos los eventos electromagnéticos dependientes del tiempo, aparece la relevancia física real del concepto de campo eléctrico. Considere la fuerza entre dos cargas distantes en movimiento acelerado, q ₁ y q ₂ . La velocidad a la que una señal o información puede viajar de un lugar a otro es ahora igual a c, la velocidad de la luz. Como resultado, cualquier movimiento de q ₁ , en q ₂no puede tener un efecto instantáneo. Entre el efecto (fuerza sobre q2) y la causa (movimiento de q1), habrá un retraso temporal. El concepto de campo eléctrico (estrictamente, campo electromagnético) es intuitivo y extremadamente útil en este contexto. La imagen del campo es la siguiente: el movimiento acelerado de la carga q1 genera ondas electromagnéticas, que se propagan en c, llegan a q2 y ejercen una fuerza sobre q2. El retardo de tiempo se explica elegantemente por el concepto de campo. A pesar de que los campos eléctricos y magnéticos solo pueden identificarse por sus efectos (fuerzas) sobre las cargas, se consideran cosas físicas en lugar de abstracciones matemáticas. Tienen su propia dinámica, es decir, evolucionan según su propio conjunto de reglas. También son capaces de transportar energía. De este modo, una fuente de campos electromagnéticos dependientes del tiempo que se encienden por un corto tiempo y luego se apagan, deja campos electromagnéticos que se propagan y transportan energía. Faraday fue el primero en establecer el concepto de campo, y es hoy uno de los conceptos más importantes de la física.

Problemas de muestra

Problema 1: Dos partículas con cargas de +4 μC y -9 μC se mantienen fijas a una distancia de 20 cm entre sí. Localice el punto en el que el campo eléctrico resultante debido al sistema de dos cargas puntuales es cero.

Solución:

El punto nulo es el punto en el que el campo eléctrico resultante debido al sistema dado de cargas puntuales es cero. Sabemos que en un sistema con dos cargas puntuales, el punto nulo está en la línea que conecta las dos cargas, y que el punto nulo siempre está más cerca de la carga de menor magnitud. El punto nulo no estará en el espacio entre las cargas ya que las dos cargas son de naturaleza opuesta.

Suponga que el campo eléctrico en el punto P es cero. El punto P está a una distancia x de la carga +4C. El campo desaparece en el punto P, por lo que las magnitudes de los campos separados producidos por las dos cargas puntuales en P deben ser iguales (y direcciones antiparalelas).

$|E_1|=|E_2|\\ \frac{k(4\text{ }\mu\text{C})}{x^2}=\frac{k(9\text{ }\mu\text{C})}{(20+x)^2}\\ \frac{4}{x^2}=\frac{9}{(20+x)^2}\\ \left(\frac{20+x}{x}\right)^2=\left(\frac{3}{2}\right)^2\\ \frac{20+x}{x}=\pm\frac{3}{2}\\ 40+2x=\pm3x\\ x=+40\text{ and}-8$

Debido a que no existe la posibilidad de un punto nulo en la región entre las dos cargas, se debe ignorar el valor negativo de x. Como resultado, el punto cero del campo eléctrico se ubica en la línea que conecta las dos cargas puntuales, 40 cm a la izquierda de la partícula cargada positivamente.

Problema 2: una carga puntual de -2 μC está ubicada en el punto A (2,2,2), luego encuentre el vector de intensidad del campo eléctrico en el punto B (1,1,1).

Solución:

El vector de intensidad de campo eléctrico debido a una carga puntual q en una posición r se puede expresar como,

$\overrightarrow{E}=\frac{kq}{r^3}\overrightarrow{r}$

El vector de posición del punto de cálculo del campo eléctrico con respecto al punto de ubicación de la fuente de carga puntual es r, y el signo propio es q.

$\overrightarrow{r}=\overrightarrow{r}_B-\overrightarrow{r}_A\\ \overrightarrow{r}=(\hat{i}+\hat{j}+\hat{k})-(2\hat{i}+2\hat{j}+2\hat{k})\\ \overrightarrow{r}=-(\hat{i}+\hat{j}+\hat{k})\\ |r|=\sqrt{(-1)^2+(-1)^2+(-1)^2}\\ |r|=\sqrt{1+1+1}\\ |r|=\sqrt{3}$

Por lo tanto, el campo eléctrico en el punto B es

$\overrightarrow{E}=\frac{kq}{r^3}\overrightarrow{r}$

Sustituye el valor en la fórmula anterior,

$\overrightarrow{E}=\frac{(9\times10^9)(-2\times10^{-6})}{(\sqrt{3})^3}(-\hat{i}-\hat{j}-\hat{k})\\ \overrightarrow{E}=\frac{(9\times10^9)(-2\times10^{-6})}{3\sqrt{3}}(-\hat{i}-\hat{j}-\hat{k})\\ \overrightarrow{E}=(-2\sqrt{3}\times10^3)(-\hat{i}-\hat{j}-\hat{k})\text{ N/C}$

Problema 3: ¿Cuál es la fuerza entre dos pequeñas esferas cargadas con cargas de 2 x 10-7 C y 3 x 10-7 C colocadas a 30 cm de distancia en el aire?

Solución:

Dado,

La magnitud de la fuerza repulsiva es 6 × 10 ^-3 N.

Carga en la primera esfera, q ₁ es 2 × 10 ^-7 C.

Carga en la segunda esfera, q ₂ es 3 × 10 ^-7 C.

Distancia entre las esferas, r es de 30 cm, es decir, 0,3 m.

La expresión de la fuerza electrostática entre las esferas se puede escribir como,

$F=\frac{q_1q_2}{4\pi\epsilon_0r^2}$

Sustituye el valor en la fórmula anterior,

$F=\frac{(9\times10^9)(6\times10^{-3})(2\times10^{-7})}{(0.3)^2}\\ F=6\times10^{-3}\text{ N}$

Por lo tanto, la fuerza entre las dos pequeñas esferas cargadas es de 6 × 10 ^–3 N. Las cargas son de la misma naturaleza. Por lo tanto, la fuerza entre ellos será repulsiva.

Problema 4: Explique el significado de la afirmación ‘la carga eléctrica de un cuerpo está cuantizada’.

Solución:

La carga eléctrica de un cuerpo está cuantificada. Esto significa que solo se puede transportar un número entero de electrones (1, 2,…, n) de una sustancia a otra. La transferencia de cargos no es fraccionaria. Como resultado, un cuerpo solo puede tener carga total en múltiplos enteros de carga eléctrica.

Las cargas utilizadas en cargas macroscópicas o de gran escala son enormes en comparación con la magnitud de la carga eléctrica. Como resultado, a escala macroscópica, la cuantificación de la carga eléctrica es inútil. Como resultado, se pasa por alto y se supone que la carga eléctrica es constante.

Problema 5: Cuando se frota una varilla de vidrio con un paño de seda, aparecen cargas en ambas. Un fenómeno similar se observa con muchos otros pares de cuerpos. Explique cómo esta observación es consistente con la ley de conservación de la carga.

Solución:

Debido a que las cargas se forman en pares, el frotamiento produce cargas de igual magnitud pero de naturaleza opuesta en los dos cuerpos. Carga por fricción es el nombre de este tipo de carga. El sistema de dos cuerpos frotados tiene una carga neta de cero. Esto se debe al hecho de que cantidades iguales de cargas opuestas se anulan entre sí. Al frotar un paño de seda sobre una varilla de vidrio, se desarrollan cargas de naturaleza opuesta en ambos cuerpos. Estos fenómenos están de acuerdo con la ley de conservación de la energía. Muchos otros pares de cuerpos exhiben un fenómeno similar.

Publicación traducida automáticamente

Artículo escrito por anoopraj758 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA