La distribución de Bernoulli es un caso especial de distribución binomial en el que solo se realiza una prueba. Es una distribución de probabilidad discreta para un ensayo de Bernoulli (un ensayo que tiene sólo dos resultados, es decir, éxito o fracaso). Por ejemplo, se puede representar como un lanzamiento de moneda donde la probabilidad de obtener cara es 0.5 y obtener cruz es 0.5. Es una distribución de probabilidad de una variable aleatoria que toma el valor 1 con probabilidad p y el valor 0 con probabilidad q=1-p . La distribución de Bernoulli es un caso especial de la distribución binomial con n=1.
La función de masa de probabilidad f de esta distribución, sobre los posibles resultados k, viene dada por:
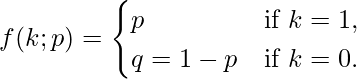
La relación anterior también se puede expresar como:
![]()
En el lenguaje de programación R, hay 4 funciones integradas para la distribución de Bernoulli y todas ellas se analizan a continuación.
dbern()
La función dbern() en la programación R mide la función de densidad de la distribución de Bernoulli.
Sintaxis: dbern(x, prob, log = FALSO)
Parámetro:
- x: vector de cuantiles
- prob: probabilidad de éxito en cada ensayo
- registro: lógico; si es VERDADERO, las probabilidades p se dan como log(p)
En estadística, viene dada por la siguiente fórmula:
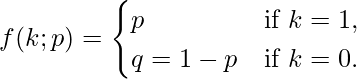
Ejemplo:
R
# import Rlab library library(Rlab) # x values for the # dbern( ) function x <- seq(0, 10, by = 1) # using dbern( ) function # to x to obtain corresponding # Bernoulli PDF y <- dbern(x, prob = 0.7) # plot dbern values plot(y, type = "o")
Producción:

pbern()
Función pbern( ) en la programación en R dada la función de distribución para la distribución de Bernoulli. La función de distribución o función de distribución acumulada (CDF) o función de frecuencia acumulada, describe la probabilidad de que una variable X tome un valor menor o igual que un número x.
Sintaxis: pbern(q, prob, lower.tail = TRUE, log.p = FALSE)
Parámetro:
- q: vector de cuantiles
- prob: probabilidad de éxito en cada ensayo
- lowe.tail: lógico
- registro.p: lógico; si es VERDADERO, las probabilidades p se dan como log(p).
Ejemplo:
R
# import Rlab library library(Rlab) # x values for the # pbern( ) function x <- seq(0, 10, by = 1) # using pbern( ) function # to x to obtain corresponding # Bernoulli CDF y <- pbern(x, prob = 0.7) # plot pbern values plot(y, type = "o")
Producción:

El gráfico anterior representa la función de distribución acumulativa de la distribución de Bernoulli en R.
qbern()
qbern() proporciona la función cuantil para la distribución de Bernoulli. Una función cuantil en términos estadísticos especifica el valor de la variable aleatoria de modo que la probabilidad de que la variable sea menor o igual a ese valor es igual a la probabilidad dada.
Sintaxis: qbern(p, prob, lower.tail = TRUE, log.p = FALSE)
Parámetro:
- p: vector de probabilidades.
- prob: probabilidad de éxito en cada intento.
- cola inferior: lógica
- registro.p: lógico; si es VERDADERO, las probabilidades p se dan como log(p).
Ejemplo:
R
# import Rlab library library(Rlab) # x values for the # qbern( ) function x <- seq(0, 1, by = 0.2) # using qbern( ) function # to x to obtain corresponding # Bernoulli QF y <- qbern(x, prob = 0.5,lower.tail = TRUE, log.p = FALSE) # plot qbern values plot(y, type = "o")
Producción:

rbern()
La función rbern() en la programación R se usa para generar un vector de números aleatorios que se distribuyen en Bernoulli.
Sintaxis: rbern(n, prob)
Parámetro:
- n: número de observaciones.
- prob : número de observaciones.
Ejemplo:
R
# import Rlab library library(Rlab) set.seed(98999) # sample size N <- 1000 # generate random variables using # rbern( ) function random_values <- rbern(N, prob = 0.5) # print the values print(random_values) # plot of randomly # drawn density hist(random_values,breaks = 10,main = "")
Producción:
[1] 0 0 1 1 0 0 0 0 0 1 0 0 0 1 0 1 1 0 1 0 1 1 1 0 1 0 1 1 0 1 0 1 1 0 1 1 1 1 0 1 0 0 0 0 1 1 1 0 1 1 1 1 1 1 0 0 0 0 1 0 0 0 0 0 0 0 1
[68] 1 1 1 0 0 1 0 1 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 1 0 0 0 1 1 0 1 1 1 1 0 1 0 0 0 0 1 0 0 1 1 0 0 0 0 0 1 0 1 0 0 1 0 1 0 1 0 1 1 1 0 1
[135] 0 0 0 0 0 1 1 0 1 1 1 1 0 0 0 0 0 1 1 0 0 0 1 1 1 1 1 0 1 1 0 0 1 0 0 1 0 1 1 0 1 1 0 1 1 1 1 1 0 0 1 0 0 0 0 1 1 0 0 0 0 0 1 1 0 0 0
[202] 1 1 1 1 1 1 1 0 0 0 0 1 1 1 0 0 0 0 0 1 1 0 1 1 0 0 1 0 0 1 1 1 0 1 1 0 1 1 0 0 0 0 0 0 0 1 1 0 0 1 1 0 0 1 1 1 1 1 0 1 1 1 1 1 0 1 0
[269] 0 0 1 1 0 1 0 1 0 1 0 0 0 0 1 1 0 0 1 1 1 1 0 0 1 0 0 1 0 0 0 0 0 1 1 0 0 1 0 0 1 0 1 0 1 0 1 0 0 0 1 0 0 1 1 0 1 0 1 0 0 0 0 1 0 0 0
[336] 0 0 1 0 0 1 0 1 0 1 0 0 1 0 1 0 1 1 1 1 0 0 0 0 1 1 0 1 1 1 1 1 1 1 1 1 0 0 1 1 1 0 1 1 0 1 0 1 0 0 1 0 1 1 0 1 1 1 0 0 1 0 1 1 0 0 0
[403] 1 0 1 0 0 1 1 0 1 1 1 1 0 1 1 1 0 1 0 0 1 0 1 0 1 0 0 0 0 1 1 0 0 0 0 1 1 1 1 1 0 0 1 0 0 1 0 0 0 0 1 0 1 1 0 0 0 1 1 0 1 1 1 0 1 0 1
[470] 1 0 1 1 1 0 0 0 0 1 0 0 0 0 1 1 1 1 1 0 0 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 1 1 1 1 0 0 1 1 0 0 1 0 1 0 1 1 1 1 1 0 1 1 0
[537] 0 0 1 0 0 0 1 1 0 0 1 0 1 1 1 0 1 1 1 1 1 0 1 1 1 0 1 0 1 0 0 1 1 1 0 0 1 1 0 1 0 0 1 1 0 1 1 0 1 1 1 0 0 0 0 0 1 1 0 1 1 1 1 0 0 1 0
[604] 1 0 1 0 1 1 0 0 0 1 0 1 0 0 0 0 0 0 1 0 0 0 0 1 1 1 1 0 1 0 0 1 0 0 0 1 0 1 0 1 1 0 1 1 1 0 1 1 1 0 1 0 1 1 0 0 0 0 1 0 0 1 0 1 0 1 1
[671] 0 0 0 1 0 1 0 0 1 0 0 0 0 1 1 1 0 1 0 1 1 0 1 1 1 0 1 1 0 1 0 0 0 0 0 0 1 0 0 1 1 0 1 1 1 1 0 1 0 1 1 1 1 1 1 1 1 1 1 0 0 0 1 0 0 1 1
[738] 1 0 0 1 1 1 1 1 0 0 1 0 1 0 0 0 1 1 0 0 0 1 0 1 0 0 0 0 0 1 0 1 1 0 0 0 0 0 0 0 0 1 0 0 0 1 1 1 0 1 0 1 0 1 1 1 1 1 1 0 1 0 1 1 0 1 1
[805] 0 1 0 1 0 1 1 0 0 1 1 1 1 0 1 1 1 0 0 0 0 1 0 0 1 1 0 0 1 1 0 0 0 1 1 1 0 0 1 0 1 0 0 0 0 1 0 1 1 0 0 0 0 1 1 0 1 0 1 1 0 1 0 1 1 1 1
[872] 1 1 0 1 0 0 1 0 0 1 1 0 1 0 0 1 0 0 0 0 0 1 1 1 0 1 1 0 0 1 1 1 0 1 0 0 1 0 1 1 1 0 1 0 0 0 1 1 0 0 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 0 0
[939] 1 1 1 1 0 1 0 0 1 1 1 0 1 0 0 1 1 0 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 1 0 1 0 0 0 0 0 1 1 0 0 1 0 0 1 1 0 0 0 1 1 1 0 0 0 0 1

El gráfico anterior representa números extraídos aleatoriamente de la distribución de Bernoulli en R.
Publicación traducida automáticamente
Artículo escrito por misraaakash1998 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA