Estrías cúbicas naturales – Barcelona Geeks

Interpolación cúbica:

La spline cúbica es una spline que usa el polinomio de tercer grado que satisface los m puntos de control dados. Para derivar las soluciones para el spline cúbico, asumimos la segunda derivación 0 en los puntos finales, lo que a su vez proporciona una condición límite que suma dos ecuaciones a m-2 ecuaciones para hacerlas solucionables. El sistema de ecuaciones para el spline cúbico para 1 dimensión puede estar dado por:

$S_i (x) = a_i + b_i *x + c_i * x^{2} + d_i x^{3}$

ranura

- El dominio de s está en intervalos de [a, b].
- S, S’, S” son todas funciones continuas en [a,b].

$S(x) =\begin{bmatrix} S_0 (x), x \epsilon [x_0, x_1] \\ S_1 (x), x \epsilon [x_1, x_2] \\ ... \\ ... \\ ... \\ S_{n-1} (x), x \epsilon [x_1, x_2] \end{bmatrix}$

Aquí S _i (x) es el

Dado que hay n intervalos y 4 coeficientes de cada ecuación, para eso necesitamos 4n parámetros para resolver el spline, podemos obtener 2n ecuaciones del hecho de que cada una de las ecuaciones del spline cúbico debe satisfacer el valor en ambos extremos:

$S_i(x_i) = y_i \\ S_i(x_{i+1}) = y_{i+1}$

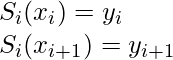
continuas y diferenciables, pero también tienen derivadas primera y segunda definidas que también son continuas en los puntos de control.

$S_{i-1}^{'}(x_i) = S_{i}^{'}(x_i)$

$S_{i-1}^{''}(x_i) = S_{i}^{''}(x_i)$

For 1, 2, 3…n-1 proporciona las restricciones de la ecuación 2n -2 . Entonces, necesitamos 2 ecuaciones más para resolver el spline cúbico anterior. Para ello, utilizaremos algunas condiciones de contorno naturales.

Estrías cúbicas naturales:

En Spline cúbico natural, asumimos que la segunda derivada de la spline en los puntos límite es 0:

$S^{''}(x_0) = 0 \\ S^{''}(x_n) = 0$

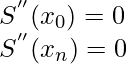
Ahora, dado que S(x) es un polinomio de tercer orden, sabemos que S”(x) es un spline lineal que se interpola. Por lo tanto, primero construimos S”(x) y luego lo integramos dos veces para obtener S(x).

Ahora, supongamos que t_i = x_i para i= 0, 1,…n, y $z_i = S^{''}(x_i), i=0,1,2..n$ y de la condición de contorno natural $z_0= z_n =0$ . La diferenciación dos veces de una spline cúbica da una spline lineal que se puede escribir como:

$S_i^{''}(x) = z_i \frac{x- t_{i+1}}{t_i - t_{i+1}} + z_{i+1} \frac{x - t_i}{t_{i+1} - t_i}$

dónde,

$h_i = t_{i+1} - t_i ; t=0,1, 2,...,n$

Ahora, la ecuación se convierte en:

$S''(x) = z_{i+1} \frac{x- t_i}{h_i} + z_{i} \frac{t_{i+1} - x}{h_i}$

Integrando esta ecuación dos veces para obtener el spline cúbico:

$S(x) =\frac{z_{i+1}}{6h_i}(x - t_i)^{3} + \frac{z_{i}}{6h_i}( t_{i+1} - x)^{3} + C_i(x_i -t) + D_i(t_{i+1} -x)$

dónde,

$C_i = \frac{y_{i+1}}{h_i} - \frac{z_{i+1} * h_i}{6} \\ D_i = \frac{y_{i}}{h_i} - \frac{z_{i} * h_i}{6}$

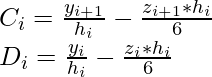
Ahora, para verificar la continuidad de la derivada en t_i, es decir, S^{‘}_{i}(t_i) = S^{‘}_{i-1}(t_{i}). Primero necesitamos encontrar derivadas y poner esa condición:

$S'(x) = \frac{z_{i+1}}{2h_i}(x - t_i)^{2} - \frac{z_{i}}{2h_i}( t_{i+1} - x)^{2} + \frac{1}{h_i}(y_{i+1}-y_i)- \frac{h_i}{6}(z_{i+1} -z_i)$

dónde,

$b_i = \frac{1}{h_i}(y_{i+1}-y_i)$

Poniendo la ecuación anterior para la continuidad y resolviéndola da la siguiente ecuación:

$6(b_i -b_{i-1}) = h_{i-1}z_{i-1} + 2(h_{i-1} + h_i)z_i + h_{i}z_{i+1}$

Tome, v_i = 6(b_i – b_{i-1}) y la ecuación anterior se puede escribir como forma de array:

$\begin{bmatrix} 1& 0 & 0& .& .& .& .& .& .& .& .& 0& \\ h_0& 2(h_0 + h_1)& h_1& & & & & & & & & .& \\ .& h_1 & 2(h_1 + h_2)& h_2& & & & & & & & .& \\ .& .& .& .& & & & & & & & .& \\ .& & & .& .& .& & & & & & .& \\ .& & & & .& .& .& & & & & .& \\ .& & & & & .& .& .& & & & .& \\ .& & & & & & .& .& .& & & .& \\ .& & & & & & & & .& h_{n-2}& 2(h_{n-1} + h_{n-2})& h_{n-1}& \\ 0& .& .& .& .& .& .& .& .& 0& 0& 1& \\ \end{bmatrix} \begin{bmatrix} z_0 \\ z_1\\ z_2\\ .\\ .\\ .\\ .\\ .\\ z_{n-1}\\ z_{n} \end{bmatrix} = \begin{bmatrix} 0\\ v_1 \\ .\\ .\\ .\\ .\\ .\\ .\\ v_{n-1}\\ 0 \end{bmatrix}$

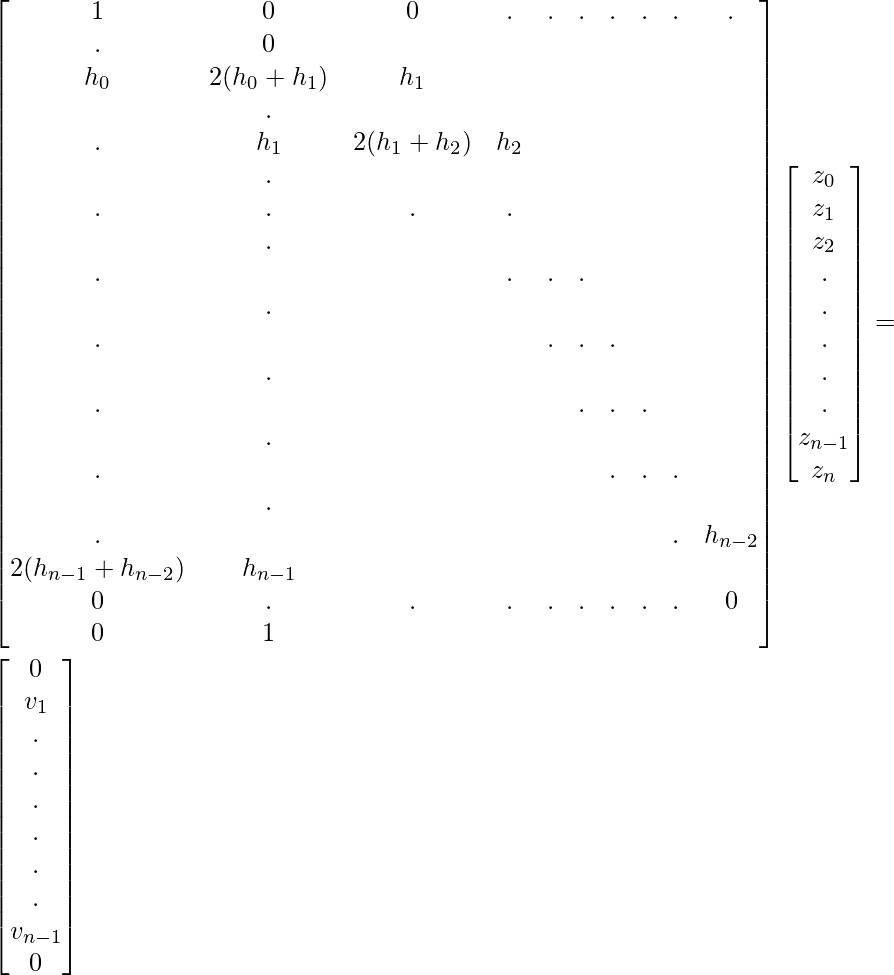
Implementación

En esta implementación, realizaremos la interpolación spline para la función f(x) = 1/x para los puntos b/w 2-10 con spline cúbico que satisfizo la condición de contorno natural.

Python3

#imports
import matplotlib.pyplot as plt
import numpy as np
from scipy.interpolate import CubicSpline, interp1d
plt.rcParams['figure.figsize'] =(12,8)
  
x = np.arange(2,10)
y = 1/(x)
# apply cubic spline interpolation
cs = CubicSpline(x, y, extrapolate=True)
# apply natural cubic spline interpolation
ns = CubicSpline(x, y,bc_type='natural', extrapolate=True)
  
# Apply Linear interpolation
linear_int = interp1d(x,y)
  
xs = np.arange(2, 9, 0.1)
ys = linear_int(xs)
  
# plot linear interpolation
plt.plot(x, y,'o', label='data')
plt.plot(xs,ys,  label="interpolation", color='green')
plt.legend(loc='upper right', ncol=2)
plt.title('Linear Interpolation')
plt.show()
  
# define a new xs
xs = np.arange(1,15)
#plot cubic spline and natural cubic spline
plt.plot(x, y, 'o', label='data')
plt.plot(xs, 1/(xs), label='true')
plt.plot(xs, cs(xs), label="S")
plt.plot(xs, ns(xs), label="NS")
plt.plot(xs, ns(xs,2), label="NS''")
plt.plot(xs, ns(xs,1), label="NS'")
  
plt.legend(loc='upper right', ncol=2)
plt.title('Cubic/Natural Cubic Spline Interpolation')
plt.show()
  
# check for boundary condition
print("Value of double differentiation at boundary conditions are %s and %s"
      %(ns(2,2),ns(10,2)))

Producción:

Value of double differentiation at boundary conditions are -1.1102230246251565e-16 and -0.00450262550915248

Interpolación linear

Interpolación spline cúbica/natural

Referencias:

Universidad NTNU de spline cúbico natural

Publicación traducida automáticamente

Artículo escrito por pawangfg y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Interpolación cúbica:

Estrías cúbicas naturales:

Implementación

Python3

Referencias:

Deja una respuesta Cancelar la respuesta