función beta – Barcelona Geeks

La función Beta es una función única y también se llama el primer tipo de integrales de Euler. La función beta se define en los dominios de los números reales. La notación para representarlo es “β”. La función beta se denota por β(p, q), donde los parámetros p y q deben ser números reales.

Explica la asociación entre el conjunto de entradas y las salidas. Cada valor de entrada de la función beta está fuertemente asociado con un valor de salida. La función beta juega un papel importante en muchas operaciones matemáticas.

La función beta se define por-
$\beta(p, q) = \int_{0}^{1}x^{p-1}(1-x)^{q-1}dx$ donde p>0 y q>0

Algunos resultados estándar:

Simetría :
$\beta(p, q) = \beta(q, p)$
$\beta(p, q) = \int_{0}^{1}x^{p-1}(1-x)^{q-1}dx$
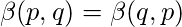
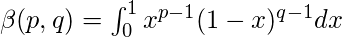
Poner x=1-y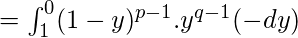
$=\int_{1}^{0}(1-y)^{p-1}.y^{q-1}(-dy)$
$=\int_{0}^{1}y^{q-1}(1-y)^{p-1}dy = \beta(q, p)$
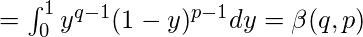
Función beta en términos de funciones trigonométricas:
$\beta(p, q) = 2\int_{0}^{\pi/2}\sin^{2p-1}x.\cos^{2q-1}xdx$
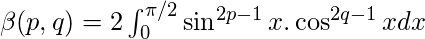
Función beta expresada como integral impropia:
$\beta(p, q) = \int_{0}^{\infty} \frac{y^{p-1}}{(1+y)^{p+q}}dy$
$= \int_{0}^{\infty} \frac{y^{q-1}}{(1+y)^{p+q}}dy$
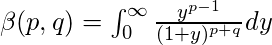
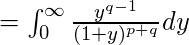
Relación entre las funciones beta y gamma:
$\beta(p, q) = \frac{\Gamma(p)\Gamma(q)}{\Gamma(p+q)}$
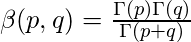
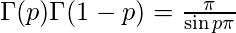$\Gamma(p)\Gamma(1-p) = \frac{\pi}{\sin p\pi}$ donde 0<p<1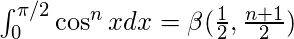
$\int_{0}^{\pi/2}\cos^n x dx = ½ \beta(\frac{1}{2}, \frac{n+1}{2})$
$\int_{0}^{\pi/2}\sin^n x dx = ½ \beta(\frac{n+1}{2}, \frac{1}{2})$
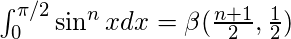
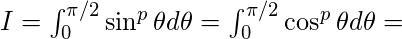
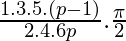- $\frac{1.3.5….(p-1)}{2.4.6…p}.\frac{\pi}{2}$ si p es un entero positivo par
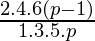- $\frac{2.4.6…(p-1)}{1.3.5….p}$ si p es un entero positivo impar
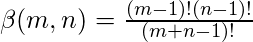$\beta(m, n) = \frac{(m-1)!(n-1)!}{(m+n-1)!}$ para m, n enteros positivos

Ejemplo-1:
Evaluar $\beta(\frac{5}{2}, \frac{3}{2}).$

Explicación:
Usando el resultado (4) obtenemos,
$\beta(\frac{5}{2}, \frac{3}{2})=\frac{\Gamma(5/2)\Gamma(3/2)}{\Gamma(5/2+3/2)}$
Sabemos que $\Gamma(p+1)=p\Gamma(p)$
Así obtenemos $\frac{3/2 \Gamma(\frac{3}{2})\Gamma(\frac{3}{2})}{3!}$
$=\frac{1}{4}(\frac{1}{2} \Gamma(\frac{1}{2}))^2=\frac{1}{4}\frac{1}{4}\pi$
=0.1964

Ejemplo-2:
Evaluar $\int_{0}^{\pi/2}\sin^{10} \theta d\theta.$

Explicación:
Como p=10 es un número entero positivo, usando el resultado (8(i)) obtenemos,
$\int_{0}{\pi/2}\sin^{10} \theta d\theta = \frac{1.3.5.7.9}{2.4.6.8.10}.\frac{\pi}{2}$
$=\frac{63\pi}{256}$

Ejemplo-3:
Evaluar $\int_{0}^{\pi/2}\cos^9 \theta d\theta.$

Explicación:
Como p=9 es un número entero positivo impar, usando el resultado 8(ii) obtenemos,
$\int_{0}^{\pi/2}\cos^9 \theta d\theta = \frac{2.4.6.8}{1.3.5.7.9}$
$=\frac{384}{945}$

Publicación traducida automáticamente

Artículo escrito por mohitg593 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta