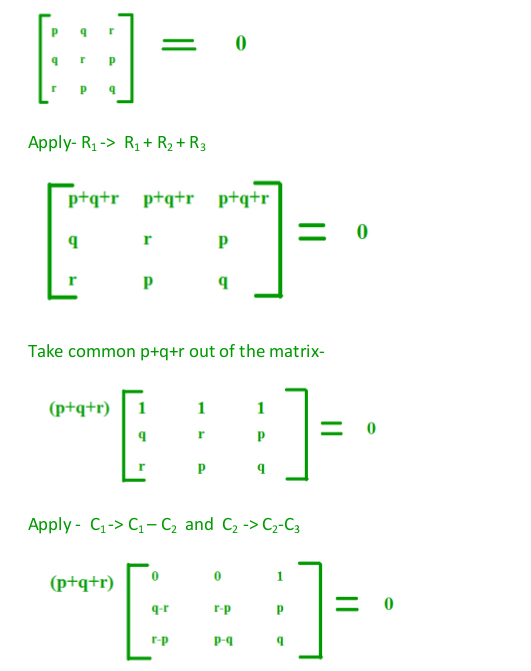
Si el siguiente sistema tiene solución no trivial,
px + qy + rz = 0 qx + ry + pz = 0 rx + py + qz = 0
Entonces, ¿cuál de las siguientes opciones es verdadera?
(A) p – q + r = 0 o p = q = –r
(B) p + q – r = 0 o p = –q = r
(C) p + q + r = 0 o p = q = r
(D) p – q + r = 0 o p = –q = –r
Respuesta: (C)
Explicación: Para una solución no trivial, |A| debe ser igual a 0
Por lo tanto,
Ahora resuélvelo usando reglas de array:
(p+q+r) [(qr)(pq) – (rp) (rp) ] = 0
Ya sea (p+q+r) = 0 o [(qr)(pq) – (rp) (rp) = 0
De (p+q+r) =0, se puede decir claramente que la opción C es la correcta.
y para una respuesta más precisa, resolvamos la segunda ecuación:
[(qr)(pq) – (rp) (rp) = 0
(qr)(pq) = (rp) (rp)
y solo p = q = r satisface esta ecuación. Entonces la opción C es la correcta.
Esta explicación ha sido aportada por Nitika Bansal.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA