Funcionamiento interno de Set en Python

Los conjuntos y su conjunto de trabajo en Python se pueden definir como la colección de elementos. En Python, estos se usan básicamente para incluir pruebas de membresía y eliminar entradas duplicadas. La estructura de datos utilizada en esto es Hashing , una técnica popular para realizar inserción, eliminación y recorrido en O(1) en promedio. Las operaciones en Hash Table son algo similares a las de Linked List. Los conjuntos en python son una lista desordenada con elementos duplicados eliminados. 

Los métodos básicos en conjuntos son : –

Creación de conjuntos : – En Python, los conjuntos se crean a través de la función set(). Se crea una lista vacía. Tenga en cuenta que el conjunto vacío no se puede crear a través de {}, crea un diccionario. 

Comprobar si un elemento está en: La complejidad temporal de esta operación es O(1) en promedio. Sin embargo, en el peor de los casos puede convertirse en O(n). 

Agregar elementos : – La inserción en el conjunto se realiza a través de la función set.add(), donde se crea un valor de registro apropiado para almacenar en la tabla hash. Igual que verificar un artículo, es decir, O(1) en promedio. Sin embargo, en el peor de los casos puede convertirse en O(n). 

Unión : – Se pueden fusionar dos conjuntos usando la función union() o | operador. Se accede a ambos valores de la tabla hash y se recorren con la operación de fusión realizada en ellos para combinar los elementos, al mismo tiempo que se eliminan los duplicados. La complejidad temporal de esto es O (len (s1) + len (s2)) donde s1 y s2 son dos conjuntos cuya unión debe realizarse. 

Intersección : – Esto se puede hacer a través de la intersection() o el operador &. Se seleccionan elementos comunes. Son similares a la iteración sobre las listas Hash y la combinación de los mismos valores en ambas tablas. La complejidad temporal de esto es O(min(len(s1), len(s2)) donde s1 y s2 son dos conjuntos cuya unión debe hacerse. 

Diferencia : – Para encontrar la diferencia entre conjuntos. Similar a encontrar la diferencia en la lista enlazada. Esto se hace a través del operador difference() o –. La complejidad temporal de encontrar la diferencia s1 – s2 es O(len(s1)) 

Diferencia simétrica : – Para encontrar elementos en ambos conjuntos, excepto los elementos comunes. Se utiliza el operador ^. La complejidad temporal de s1^s2 es O(len(s1)) 

Actualización de diferencia simétrica : devuelve un nuevo conjunto que contiene una diferencia simétrica de dos conjuntos. La complejidad del tiempo es O(len(s2)) clear :- Borra el conjunto o la tabla hash. 

Fuente de complejidad temporal: Python Wiki 

Si hay varios valores presentes en la misma posición de índice, el valor se agrega a esa posición de índice para formar una lista enlazada. En, los conjuntos de CPython se implementan utilizando diccionario con variables ficticias, donde la clave es el conjunto de miembros con mayores optimizaciones a la complejidad del tiempo. Implementación de conjuntos: –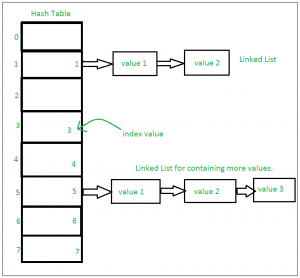  
Conjuntos con numerosas operaciones en una sola tabla hash: – 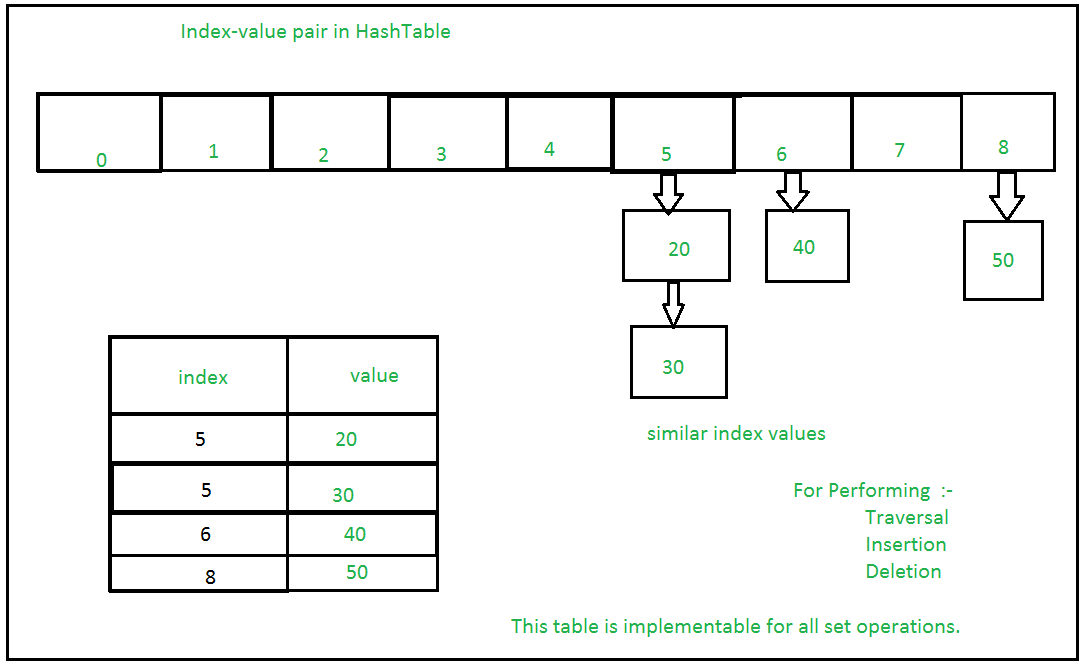Ejemplos:

# empty set, avoid using {} in creating set or dictionary is created
x = set() 

# set {'e', 'h', 'l', 'o'} is created in unordered way
B = set('hello') 

# set{'a', 'c', 'd', 'b', 'e', 'f', 'g'} is created
A = set('abcdefg') 

# set{'a', 'b', 'h', 'c', 'd', 'e', 'f', 'g'} 
A.add('h')    

fruit ={'orange', 'banana', 'pear', 'apple'}

# True  fast membership testing in sets
'pear' in fruit      

'mango' in fruit     # False

A == B       # A is equivalent to B

A != B       # A is not equivalent to B

A <= B    # A is subset of B A <B>= B    

A > B     # A is proper superset of B

A | B        # the union of A and B

A & B     # the intersection of A and B

A - B        # the set of elements in A but not B

A ˆ B        # the symmetric difference

a = {x for x in A if x not in 'abc'}   # Set Comprehension