Los métodos Dunder ( d ouble under score) en Python son métodos que se usan comúnmente para la sobrecarga de operadores. Algunos ejemplos de métodos de dunder son __init__ , __repr__ , __add__ , __str__ etc. Estos métodos son útiles para modificar el comportamiento de un objeto.
Por ejemplo, cuando se usa el operador ‘+’ entre dos números, el resultado obtenido es simplemente la suma de los dos números, mientras que cuando se usa ‘+’ entre dos strings, el resultado obtenido es la concatenación de las dos strings.
Operaciones vectoriales de uso común:
considere dos vectores vec1 y vec2 con coordenadas: vec1 = (x1, y1, z1) y vec2 = (x2, y2, z2).
- Magnitud: Magnitud de vec1 =
.
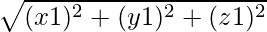- Adición: para esta operación, necesitamos el método __add__ para agregar dos objetos vectoriales.
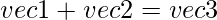donde las coordenadas de vec3 son 
.
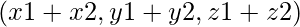- Resta: para esta operación, necesitamos el método __sub__ para restar dos objetos vectoriales.
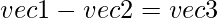donde las coordenadas de vec3 son 
.
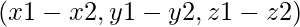- Producto escalar: Para esta operación, necesitamos el método __xor__ ya que estamos usando el símbolo ‘^’ para indicar el producto escalar.
^ 
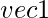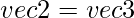donde están las coordenadas de vec3 
.
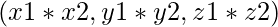- Producto cruzado: para esta operación, necesitamos el método __mul__ ya que estamos usando el símbolo ‘*’ para indicar el producto cruzado. 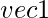* 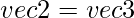donde las coordenadas de vec3 son
.
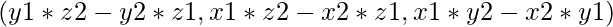Finalmente, también necesitamos un método __init__ para inicializar las coordenadas del Vector y el método __repr__ para definir la representación del objeto Vector. Entonces, cuando imprimimos nuestro objeto Vector, la salida debería ser algo como esto. print(Vector(1, -2, 3)) ==> Salida: 1i -2j + 3k
A continuación se muestra la implementación:
Python3
# Python3 program to implement 3-D Vectors.
from math import sqrt
# Definition of Vector class
class Vector:
# Initialize 3D Coordinates of the Vector
def __init__(self, x, y, z):
self.x = x
self.y = y
self.z = z
# Method to calculate magnitude of a Vector
def magnitude(self):
return sqrt(self.x ** 2 + self.y ** 2 + self.z ** 2)
# Method to add to Vector
def __add__(self, V):
return Vector(self.x + V.x, self.y + V.y, self.z + V.z)
# Method to subtract 2 Vectors
def __sub__(self, V):
return Vector(self.x - V.x, self.y - V.y, self.z - V.z)
# Method to calculate the dot product of two Vectors
def __xor__(self, V):
return self.x * V.x + self.y * V.y + self.z * V.z
# Method to calculate the cross product of 2 Vectors
def __mul__(self, V):
return Vector(self.y * V.z - self.z * V.y,
self.z * V.x - self.x * V.z,
self.x * V.y - self.y * V.x)
# Method to define the representation of the Vector
def __repr__(self):
out = str(self.x) + "i "
if self.y >= 0:
out += "+ "
out += str(self.y) + "j "
if self.z >= 0:
out += "+ "
out += str(self.z) + "k"
return out
if __name__ == "__main__":
vec1 = Vector(1, 2, 2)
vec2 = Vector(3, 1, 2)
# Magnitude of vector1
print("Magnitude of vector1:", vec1.magnitude())
# String representation of vector
print("String representation of vector1: " + str(vec1))
# Addition of two vectors
print("Addition of vector1 and vector2: " + str(vec1 + vec2))
# Subtraction of two vectors
print("Subtraction of vector1 and vector2: " + str(vec1 - vec2))
# Dot product of two vectors
print("Dot Product of vector1 and vector2: " + str(vec1 ^ vec2))
# Cross product of two vectors
print("Cross Product of vector1 and vector2: " + str(vec1 * vec2))
Magnitude of vector1: 3.0 String representation of vector1: 1i + 2j + 2k Addition of vector1 and vector2: 4i + 3j + 4k Subtraction of vector1 and vector2: -2i + 1j + 0k Dot Product of vector1 and vector2: 9 Cross Product of vector1 and vector2: 2i + 4j -5k
Publicación traducida automáticamente
Artículo escrito por rituraj_jain y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA