En teoría de grafos, la centralidad de Katz de un Node es una medida de centralidad en una red. Fue introducido por Leo Katz en 1953 y se utiliza para medir el grado relativo de influencia de un actor (o Node) dentro de una red social. A diferencia de las típicas medidas de centralidad que consideran solo el camino más corto (la geodésica) entre un par de actores, las medidas de centralidad de Katz influyen teniendo en cuenta el número total de caminatas entre un par de actores.
Es similar al PageRank de Google ya la centralidad del vector propio.
Midiendo la centralidad de Katz
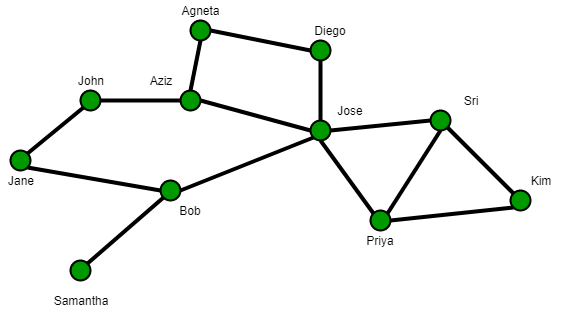
Una red social simple: los Nodes representan personas o actores y los bordes entre Nodes representan alguna relación entre actores
La centralidad de Katz calcula la influencia relativa de un Node dentro de una red midiendo el número de vecinos inmediatos (Nodes de primer grado) y también todos los demás Nodes en la red que se conectan al Node en consideración a través de estos vecinos inmediatos. Sin embargo, las conexiones realizadas con vecinos lejanos están penalizadas por un factor de atenuación ![]() . A cada ruta o conexión entre un par de Nodes se le asigna un peso determinado por
. A cada ruta o conexión entre un par de Nodes se le asigna un peso determinado por ![]() y la distancia entre Nodes como
y la distancia entre Nodes como ![]() .
.
Por ejemplo, en la figura de la derecha, suponga que se mide la centralidad de John y que ![]() . El peso asignado a cada enlace que conecta a John con sus vecinos inmediatos Jane y Bob será
. El peso asignado a cada enlace que conecta a John con sus vecinos inmediatos Jane y Bob será ![]() . Dado que Jose se conecta a John indirectamente a través de Bob, el peso asignado a esta conexión (compuesta por dos enlaces) será
. Dado que Jose se conecta a John indirectamente a través de Bob, el peso asignado a esta conexión (compuesta por dos enlaces) será ![]() . Del mismo modo, el peso asignado a la conexión entre Agneta y John a través de Aziz y Jane será
. Del mismo modo, el peso asignado a la conexión entre Agneta y John a través de Aziz y Jane será ![]() y el peso asignado a la conexión entre Agneta y John a través de Diego, Jose y Bob será
y el peso asignado a la conexión entre Agneta y John a través de Diego, Jose y Bob será ![]() .
.
Formulación matemática
Sea A la array de adyacencia de una red en consideración. Los elementos![]() de A son variables que toman el valor 1 si un Node i está conectado al Node j y 0 en caso contrario. Las potencias de A indican la presencia (o ausencia) de enlaces entre dos Nodes a través de intermediarios. Por ejemplo, en matrix
de A son variables que toman el valor 1 si un Node i está conectado al Node j y 0 en caso contrario. Las potencias de A indican la presencia (o ausencia) de enlaces entre dos Nodes a través de intermediarios. Por ejemplo, en matrix![]() , if element
, if element![]() , indica que el Node 2 y el Node 12 están conectados a través de algunos vecinos de primer y segundo grado del Node 2. If
, indica que el Node 2 y el Node 12 están conectados a través de algunos vecinos de primer y segundo grado del Node 2. If![]() denota la centralidad de Katz de un Node i, entonces matemáticamente:
denota la centralidad de Katz de un Node i, entonces matemáticamente:
![]()
Note that the above definition uses the fact that the element at location ![]() of the adjacency matrix
of the adjacency matrix ![]() raised to the power
raised to the power ![]() (i.e.
(i.e. ![]() ) reflects the total number of
) reflects the total number of ![]() degree connections between nodes
degree connections between nodes ![]() and
and ![]() . The value of the attenuation factor
. The value of the attenuation factor ![]() has to be chosen such that it is smaller than the reciprocal of the absolute value of the largest eigenvalue of the adjacency matrix A. In this case the following expression can be used to calculate Katz centrality:
has to be chosen such that it is smaller than the reciprocal of the absolute value of the largest eigenvalue of the adjacency matrix A. In this case the following expression can be used to calculate Katz centrality:
![]()
Here![]() is the identity matrix,
is the identity matrix, ![]() is an identity vector of size n (n is the number of nodes) consisting of ones.
is an identity vector of size n (n is the number of nodes) consisting of ones. ![]() denotes the transposed matrix of A and (
denotes the transposed matrix of A and (![]() denotes matrix inversion of the term (
denotes matrix inversion of the term (![]() ).
).
A continuación se muestra el código para el cálculo de la Centralidad de Katz del grafo y sus diversos Nodes.
def katz_centrality(G, alpha=0.1, beta=1.0,
max_iter=1000, tol=1.0e-6,
nstart=None, normalized=True,
weight = 'weight'):
"""Compute the Katz centrality for the nodes
of the graph G.
Katz centrality computes the centrality for a node
based on the centrality of its neighbors. It is a
generalization of the eigenvector centrality. The
Katz centrality for node `i` is
.. math::
x_i = \alpha \sum_{j} A_{ij} x_j + \beta,
where `A` is the adjacency matrix of the graph G
with eigenvalues `\lambda`.
The parameter `\beta` controls the initial centrality and
.. math::
\alpha < \frac{1}{\lambda_{max}}.
Katz centrality computes the relative influence of
a node within a network by measuring the number of
the immediate neighbors (first degree nodes) and
also all other nodes in the network that connect
to the node under consideration through these
immediate neighbors.
Extra weight can be provided to immediate neighbors
through the parameter :math:`\beta`. Connections
made with distant neighbors are, however, penalized
by an attenuation factor `\alpha` which should be
strictly less than the inverse largest eigenvalue
of the adjacency matrix in order for the Katz
centrality to be computed correctly.
Parameters
----------
G : graph
A NetworkX graph
alpha : float
Attenuation factor
beta : scalar or dictionary, optional (default=1.0)
Weight attributed to the immediate neighborhood.
If not a scalar, the dictionary must have an value
for every node.
max_iter : integer, optional (default=1000)
Maximum number of iterations in power method.
tol : float, optional (default=1.0e-6)
Error tolerance used to check convergence in
power method iteration.
nstart : dictionary, optional
Starting value of Katz iteration for each node.
normalized : bool, optional (default=True)
If True normalize the resulting values.
weight : None or string, optional
If None, all edge weights are considered equal.
Otherwise holds the name of the edge attribute
used as weight.
Returns
-------
nodes : dictionary
Dictionary of nodes with Katz centrality as
the value.
Raises
------
NetworkXError
If the parameter `beta` is not a scalar but
lacks a value for at least one node
Notes
-----
This algorithm it uses the power method to find
the eigenvector corresponding to the largest
eigenvalue of the adjacency matrix of G.
The constant alpha should be strictly less than
the inverse of largest eigenvalue of the adjacency
matrix for the algorithm to converge.
The iteration will stop after max_iter iterations
or an error tolerance ofnumber_of_nodes(G)*tol
has been reached.
When `\alpha = 1/\lambda_{max}` and `\beta=0`,
Katz centrality is the same as eigenvector centrality.
For directed graphs this finds "left" eigenvectors
which corresponds to the in-edges in the graph.
For out-edges Katz centrality first reverse the
graph with G.reverse().
"""
from math import sqrt
if len(G) == 0:
return {}
nnodes = G.number_of_nodes()
if nstart is None:
# choose starting vector with entries of 0
x = dict([(n,0) for n in G])
else:
x = nstart
try:
b = dict.fromkeys(G,float(beta))
except (TypeError,ValueError,AttributeError):
b = beta
if set(beta) != set(G):
raise nx.NetworkXError('beta dictionary '
'must have a value for every node')
# make up to max_iter iterations
for i in range(max_iter):
xlast = x
x = dict.fromkeys(xlast, 0)
# do the multiplication y^T = Alpha * x^T A - Beta
for n in x:
for nbr in G[n]:
x[nbr] += xlast[n] * G[n][nbr].get(weight, 1)
for n in x:
x[n] = alpha*x[n] + b[n]
# check convergence
err = sum([abs(x[n]-xlast[n]) for n in x])
if err < nnodes*tol:
if normalized:
# normalize vector
try:
s = 1.0/sqrt(sum(v**2 for v in x.values()))
# this should never be zero?
except ZeroDivisionError:
s = 1.0
else:
s = 1
for n in x:
x[n] *= s
return x
raise nx.NetworkXError('Power iteration failed to converge in '
'%d iterations.' % max_iter)
La función anterior se invoca usando la biblioteca networkx y una vez que la biblioteca está instalada, eventualmente puede usarla y el siguiente código debe escribirse en python para la implementación de la centralidad katz de un Node.
>>> import networkx as nx
>>> import math
>>> G = nx.path_graph(4)
>>> phi = (1+math.sqrt(5))/2.0 # largest eigenvalue of adj matrix
>>> centrality = nx.katz_centrality(G,1/phi-0.01)
>>> for n,c in sorted(centrality.items()):
... print("%d %0.2f"%(n,c))
La salida del código anterior es:
0 0.37 1 0.60 2 0.60 3 0.37
El resultado anterior es un diccionario que representa el valor de la centralidad katz de cada Node. Lo anterior es una extensión de mi serie de artículos sobre las medidas de centralidad. Sigan haciendo networking!!!
Referencias
http://networkx.readthedocs.io/en/networkx-1.10/index.html
https://en.wikipedia.org/wiki/Katz_centrality
Publicación traducida automáticamente
Artículo escrito por Jayant Bisht y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA