Detección de línea en python con OpenCV | Método Houghline

La Transformada de Hough es un método que se utiliza en el procesamiento de imágenes para detectar cualquier forma, si esa forma se puede representar en forma matemática. Puede detectar la forma incluso si está rota o distorsionada un poco. 
Veremos cómo funciona la transformación de Hough para la detección de líneas usando el método de transformación de HoughLine. Para aplicar el método de Houghline, primero es deseable una detección de bordes de la imagen específica. Para conocer la técnica de detección de bordes, consulte el artículo Detección de bordes 
 

Conceptos básicos del método Houghline

Una línea se puede representar como y = mx + c o en forma paramétrica, como r = xcosθ + ysinθ donde r es la distancia perpendicular desde el origen a la línea, y θ es el ángulo formado por esta línea perpendicular y el eje horizontal medido en contador -en el sentido de las agujas del reloj (esa dirección varía según cómo represente el sistema de coordenadas. Esta representación se usa en OpenCV). 
 

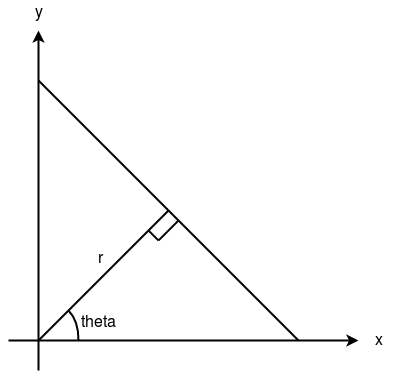
Entonces, cualquier línea se puede representar en estos dos términos, (r, θ).
Funcionamiento del método Houghline: 
 

• Primero crea una array o acumulador 2D (para contener valores de dos parámetros) y se establece en cero inicialmente.
• Deje que las filas denoten la r y las columnas denoten la (θ)theta.
• El tamaño de la array depende de la precisión que necesite. Suponga que desea que la precisión de los ángulos sea de 1 grado, necesita 180 columnas (el grado máximo para una línea recta es 180).
• Para r, la distancia máxima posible es la longitud diagonal de la imagen. Entonces, tomando una precisión de un píxel, el número de filas puede ser la longitud diagonal de la imagen.

Ejemplo: 
considere una imagen de 100 × 100 con una línea horizontal en el medio. Toma el primer punto de la línea. Conoces sus valores (x, y). Ahora en la ecuación de línea, pon los valores θ(theta) = 0,1,2,….,180 y comprueba la r que obtienes. Por cada par (r, 0), incrementa el valor en uno en el acumulador en sus celdas correspondientes (r, 0). Así que ahora en el acumulador, la celda (50,90) = 1 junto con algunas otras celdas. 
Ahora toma el segundo punto de la línea. Haz lo mismo que arriba. Incrementa los valores en las celdas correspondientes a (r,0) que obtuviste. Esta vez, la celda (50,90) = 2. En realidad estamos votando los valores (r,0). Continúa este proceso para cada punto de la línea. En cada punto, la celda (50,90) se incrementará o votará a favor, mientras que otras celdas pueden o no votarse a favor. Así, al final, la celda (50,90) tendrá el máximo de votos. Entonces, si busca en el acumulador el máximo de votos, obtiene el valor (50,90) que dice que hay una línea en esta imagen a una distancia de 50 desde el origen y en un ángulo de 90 grados. 
 

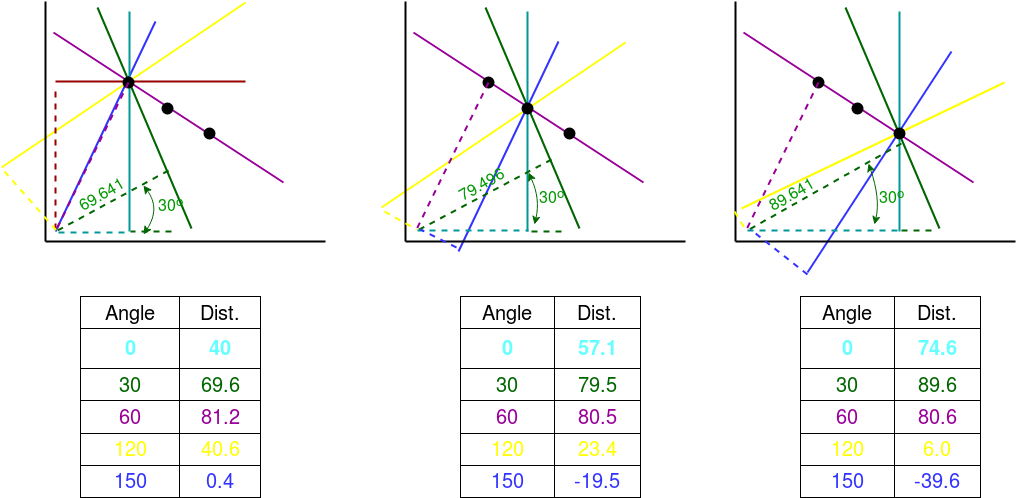
Todo lo explicado anteriormente está encapsulado en la función OpenCV, cv2.HoughLines(). Simplemente devuelve una array de valores (r, 0). r se mide en píxeles y 0 se mide en radianes. 
 

# Python program to illustrate HoughLine
# method for line detection
import cv2
import numpy as np
 
# Reading the required image in
# which operations are to be done.
# Make sure that the image is in the same
# directory in which this python program is
img = cv2.imread('image.jpg')
 
# Convert the img to grayscale
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
 
# Apply edge detection method on the image
edges = cv2.Canny(gray, 50, 150, apertureSize=3)
 
# This returns an array of r and theta values
lines = cv2.HoughLines(edges, 1, np.pi/180, 200)
 
# The below for loop runs till r and theta values
# are in the range of the 2d array
for r_theta in lines:
    arr = np.array(r_theta[0], dtype=np.float64)
    r, theta = arr
    # Stores the value of cos(theta) in a
    a = np.cos(theta)
 
    # Stores the value of sin(theta) in b
    b = np.sin(theta)
 
    # x0 stores the value rcos(theta)
    x0 = a*r
 
    # y0 stores the value rsin(theta)
    y0 = b*r
 
    # x1 stores the rounded off value of (rcos(theta)-1000sin(theta))
    x1 = int(x0 + 1000*(-b))
 
    # y1 stores the rounded off value of (rsin(theta)+1000cos(theta))
    y1 = int(y0 + 1000*(a))
 
    # x2 stores the rounded off value of (rcos(theta)+1000sin(theta))
    x2 = int(x0 - 1000*(-b))
 
    # y2 stores the rounded off value of (rsin(theta)-1000cos(theta))
    y2 = int(y0 - 1000*(a))
 
    # cv2.line draws a line in img from the point(x1,y1) to (x2,y2).
    # (0,0,255) denotes the colour of the line to be
    # drawn. In this case, it is red.
    cv2.line(img, (x1, y1), (x2, y2), (0, 0, 255), 2)
 
# All the changes made in the input image are finally
# written on a new image houghlines.jpg
cv2.imwrite('linesDetected.jpg', img)

Elaboración de función(cv2.HoughLines(edges,1,np.pi/180, 200)): 
 

1. Primer parámetro, la imagen de entrada debe ser una imagen binaria, por lo tanto, aplique la detección de borde de umbral antes de encontrar la transformación de Hough.
2. Los parámetros segundo y tercero son las precisiones r y θ(theta) respectivamente.
3. El cuarto argumento es el umbral, lo que significa el voto mínimo que debe obtener para que se considere como una línea.
4. Recuerde, el número de votos depende del número de puntos en la línea. Por lo tanto, representa la longitud mínima de línea que debe detectarse. 
    

Método alternativo más simple para extraer puntos directamente:

import cv2
import numpy as np
 
# Read image
image = cv2.imread('path/to/image.png')
 
# Convert image to grayscale
gray = cv2.cvtColor(image,cv2.COLOR_BGR2GRAY)
 
# Use canny edge detection
edges = cv2.Canny(gray,50,150,apertureSize=3)
 
# Apply HoughLinesP method to
# to directly obtain line end points
lines_list =[]
lines = cv2.HoughLinesP(
            edges, # Input edge image
            1, # Distance resolution in pixels
            np.pi/180, # Angle resolution in radians
            threshold=100, # Min number of votes for valid line
            minLineLength=5, # Min allowed length of line
            maxLineGap=10 # Max allowed gap between line for joining them
            )
 
# Iterate over points
for points in lines:
      # Extracted points nested in the list
    x1,y1,x2,y2=points[0]
    # Draw the lines joing the points
    # On the original image
    cv2.line(image,(x1,y1),(x2,y2),(0,255,0),2)
    # Maintain a simples lookup list for points
    lines_list.append([(x1,y1),(x2,y2)])
     
# Save the result image
cv2.imwrite('detectedLines.png',image)

Resumiendo el proceso

• En un contexto de análisis de imágenes, las coordenadas de los puntos de los segmentos de borde (es decir, X,Y) en la imagen son conocidas y, por lo tanto, sirven como constantes en la ecuación de línea paramétrica, mientras que R(rho) y Theta(θ) son las variables desconocidas que buscamos.
• Si graficamos los posibles valores (r) definidos por cada (theta), los puntos en el espacio de imagen cartesiana se asignan a curvas (es decir, sinusoides) en el espacio de parámetros polares de Hough. Esta transformación de punto a curva es la transformación de Hough para líneas rectas.
• La transformación se implementa cuantificando el espacio de parámetros de Hough en intervalos finitos o celdas acumuladoras. A medida que se ejecuta el algoritmo, cada (X,Y) se transforma en una curva discretizada (r,0) y las celdas del acumulador (array 2D) que se encuentran a lo largo de esta curva se incrementan.
• Los picos resultantes en la array de acumuladores representan una fuerte evidencia de que existe una línea recta correspondiente en la imagen.

Aplicaciones de la transformada de Hough: 
 

1. Se utiliza para aislar características de una forma particular dentro de una imagen.
2. Tolerante a las lagunas en las descripciones de los límites de las características y relativamente poco afectado por el ruido de la imagen.
3. Se utiliza ampliamente en el escaneo, verificación y reconocimiento de códigos de barras.

Este artículo es una contribución de Pratima Upadhyay . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.