Una imagen digital es una array bidimensional de tamaño M x N , donde M es el número de filas y N es el número de columnas de la array. Una imagen digital se compone de un número finito de elementos de imagen discretos llamados píxeles. La ubicación de cada píxel viene dada por las coordenadas (x, y) y el valor de cada píxel viene dado por el valor de intensidad f . Por tanto, los elementos de una imagen digital se pueden representar mediante f(x, y).
Resolucion espacial
El término resolución espacial corresponde al número total de píxeles en la imagen dada. Si el número de píxeles es mayor, entonces la resolución de la imagen es mayor.
muestreo descendente
En la técnica de muestreo descendente, el número de píxeles en la imagen dada se reduce dependiendo de la frecuencia de muestreo. Debido a esto, la resolución y el tamaño de la imagen disminuyen.
Muestreo ascendente
El número de píxeles en la imagen submuestreada se puede aumentar utilizando técnicas de interpolación de muestreo ascendente. La técnica de muestreo ascendente aumenta la resolución y el tamaño de la imagen.
Algunas técnicas de muestreo ascendente comúnmente utilizadas son
- Interpolación del vecino más cercano
- Interpolación bilineal
- interpolación cúbica
En este artículo, implementamos el muestreo superior mediante la interpolación del vecino más cercano mediante la replicación de filas y columnas. A medida que aumenta la frecuencia de muestreo, se verán artefactos en la imagen reconstruida.
Sin embargo, al utilizar la interpolación bilineal o la interpolación cúbica, se puede lograr una mejor calidad de la imagen reconstruida. Tanto el muestreo descendente como el muestreo ascendente se pueden ilustrar en escala de grises para una mejor comprensión porque, al leer imágenes con OpenCV , se manipulan algunos valores de color, por lo que vamos a convertir la imagen de entrada original en una imagen en blanco y negro.
El siguiente programa muestra la representación muestreada hacia abajo y muestreada hacia arriba de una imagen dada:
Python3
# Import cv2, matplotlib, numpy
import cv2
import matplotlib.pyplot as plt
import numpy as np
# Read the original image and know its type
img1 = cv2.imread('g4g.png', 0)
# Obtain the size of the original image
[m, n] = img1.shape
print('Image Shape:', m, n)
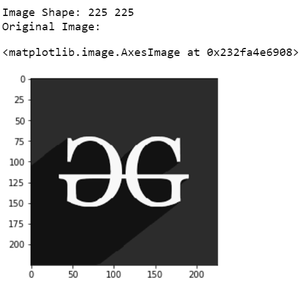
# Show original image
print('Original Image:')
plt.imshow(img1, cmap="gray")
# Down sampling
# Assign a down sampling rate
# Here we are down sampling the
# image by 4
f = 4
# Create a matrix of all zeros for
# downsampled values
img2 = np.zeros((m//f, n//f), dtype=np.int)
# Assign the down sampled values from the original
# image according to the down sampling frequency.
# For example, if the down sampling rate f=2, take
# pixel values from alternate rows and columns
# and assign them in the matrix created above
for i in range(0, m, f):
for j in range(0, n, f):
try:
img2[i//f][j//f] = img1[i][j]
except IndexError:
pass
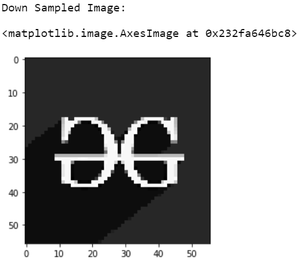
# Show down sampled image
print('Down Sampled Image:')
plt.imshow(img2, cmap="gray")
# Up sampling
# Create matrix of zeros to store the upsampled image
img3 = np.zeros((m, n), dtype=np.int)
# new size
for i in range(0, m-1, f):
for j in range(0, n-1, f):
img3[i, j] = img2[i//f][j//f]
# Nearest neighbour interpolation-Replication
# Replicating rows
for i in range(1, m-(f-1), f):
for j in range(0, n-(f-1)):
img3[i:i+(f-1), j] = img3[i-1, j]
# Replicating columns
for i in range(0, m-1):
for j in range(1, n-1, f):
img3[i, j:j+(f-1)] = img3[i, j-1]
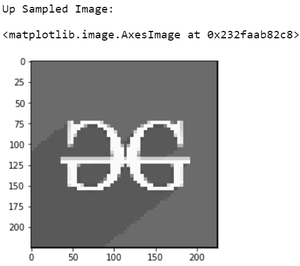
# Plot the up sampled image
print('Up Sampled Image:')
plt.imshow(img3, cmap="gray")
Aporte:

Producción: