Este artículo aborda cuestiones tanto teóricas como prácticas en Ciencias de la Computación (CS). Revisa Turing Machines (TMs), una clase fundamental de autómatas y presenta un simulador para una amplia variante de TMs: no determinista con múltiples cintas. El no determinismo se simula mediante una búsqueda en amplitud (BFS) del árbol de cálculo.
El simulador está escrito en Python 3 y aprovecha la potencia y expresividad de este lenguaje de programación, combinando técnicas de programación orientada a objetos y funcional.
La organización es la siguiente. En primer lugar, las MT se introducen de manera informal, destacando sus múltiples aplicaciones en Teórica CS. Luego, se dan las definiciones formales del modelo básico y la variante multicinta. Finalmente, se presenta el diseño e implementación del simulador, brindando ejemplos de su uso y ejecución.
Introducción
Los MT son autómatas abstractos ideados por Alan Turing en 1936 para investigar los límites de la computación. Los MT pueden calcular funciones siguiendo reglas simples.
Un TM es un modelo computacional primitivo con 3 componentes:
- Una memoria: una cinta de entrada-salida dividida en celdas discretas que almacenan símbolos. La cinta tiene una celda más a la izquierda pero no está limitada a la derecha, por lo que no hay límite en la longitud de las strings que puede almacenar.
- Una unidad de control con un conjunto finito de estados y un cabezal de cinta que apunta a la celda actual y puede moverse hacia la izquierda o hacia la derecha durante el cálculo.
- Un programa almacenado en el control finito que gobierna el cómputo de la máquina.
El funcionamiento de una MT consta de tres etapas:
- Inicialización. Se carga una string de entrada de longitud N en las primeras N celdas de la cinta. El resto de infinitas celdas contienen un símbolo especial llamado espacio en blanco. La máquina cambia al estado de inicio.
- Cálculo. Cada paso de cálculo implica:
- Lectura del símbolo en la celda actual (la que está siendo escaneada por el cabezal de la cinta).
- Siguiendo las reglas definidas por el programa para la combinación del estado actual y la lectura del símbolo. Las reglas se denominan transiciones o movimientos y consisten en: (a) escribir un nuevo símbolo en la celda actual, (b) cambiar a un nuevo estado y (c) opcionalmente mover la cabeza una celda a la izquierda o a la derecha.
- finalización. El cálculo se detiene cuando no hay una regla para el estado y el símbolo actuales. Si la máquina está en el estado final, la TM acepta la string de entrada. Si el estado actual no es final, la TM rechaza la string de entrada. Tenga en cuenta que no todos los TM llegan a esta etapa porque es posible que un TM nunca se detenga en una entrada dada, ingresando en un ciclo infinito.
Las MT tienen muchas aplicaciones en Ciencias de la Computación Teórica y están fuertemente relacionadas con la teoría del lenguaje formal. Las MT son reconocedores de idiomas que aceptan la clase superior de la jerarquía de idiomas de Chomsky: el tipo 0 de idiomas generados por gramáticas sin restricciones. También son transductores de idiomas: dada una string de entrada de un idioma, un TM puede calcular una string de salida del mismo idioma o de uno diferente. Esta capacidad permite a los MT calcular funciones cuyas entradas y salidas están codificadas como strings de un lenguaje formal, por ejemplo, los números binarios considerados como el conjunto de strings sobre el alfabeto {0, 1}.
Church-Turing afirma que las MT pueden calcular cualquier función que pueda expresarse mediante un algoritmo. Sus implicaciones son que las MT son en realidad computadoras universales que, al ser dispositivos matemáticos abstractos, no sufren las limitaciones de tiempo y espacio de las físicas. Si esta tesis es cierta, como creen muchos informáticos, el hecho descubierto por Turing de que hay funciones que no pueden ser computadas por un TM implica que hay funciones que no son algorítmicamente computables por ningún ordenador pasado, presente o futuro.
Los MT también han sido muy importantes en el estudio de la complejidad computacional y uno de los temas abiertos centrales en CS y matemáticas: el problema P vs NP. Los TM son un modelo conveniente e independiente del hardware para analizar la complejidad computacional de los algoritmos en términos de la cantidad de pasos realizados (complejidad de tiempo) o la cantidad de celdas escaneadas (complejidad de espacio) durante la computación.
Definición formal: el modelo básico
Una máquina de Turing (TM) es una tupla de 7 ![]() donde:
donde:
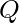 es un conjunto finito no vacío de estados.
es un conjunto finito no vacío de estados. es un conjunto finito no vacío de símbolos llamado alfabeto de cinta.
es un conjunto finito no vacío de símbolos llamado alfabeto de cinta. es el alfabeto de entrada.
es el alfabeto de entrada.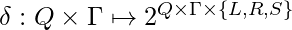 es la función de transición o siguiente movimiento que asigna pares de símbolos de estado a subconjuntos de triples estado, símbolo, dirección de la cabeza (izquierda, derecha o permanecer).
es la función de transición o siguiente movimiento que asigna pares de símbolos de estado a subconjuntos de triples estado, símbolo, dirección de la cabeza (izquierda, derecha o permanecer).
 es el estado inicial.
es el estado inicial. es el estado de aceptación final.
es el estado de aceptación final. es el símbolo en blanco.
es el símbolo en blanco.
En cada paso del cálculo, una TM puede describirse mediante una descripción instantánea (ID). Una ID es un triple ![]() donde
donde ![]() es el estado real,
es el estado real, ![]() es la string contenida en las celdas a la izquierda de la celda que está siendo escaneada por la máquina, y
es la string contenida en las celdas a la izquierda de la celda que está siendo escaneada por la máquina, y ![]() es la string contenida en la celda actual y las otras celdas a la derecha del cabezal de la cinta. hasta la celda que inicia la secuencia infinita de espacios en blanco.
es la string contenida en la celda actual y las otras celdas a la derecha del cabezal de la cinta. hasta la celda que inicia la secuencia infinita de espacios en blanco.
La relación binaria relaciona ![]() dos ID y se define de la siguiente manera, para todos
dos ID y se define de la siguiente manera, para todos ![]() y
y ![]() y
y ![]() :
:
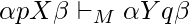 si y si
si y si 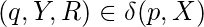
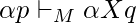 si y si
si y si 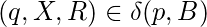
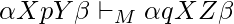 si y si
si y si 
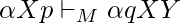 si y si
si y si 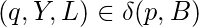
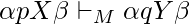 si y si
si y si 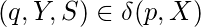
 si y si
si y si 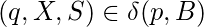
Sea ![]() el cierre transitivo y reflexivo de
el cierre transitivo y reflexivo de ![]() , es decir, la aplicación de cero o más transiciones entre ID. Entonces, el lenguaje reconocido por
, es decir, la aplicación de cero o más transiciones entre ID. Entonces, el lenguaje reconocido por ![]() se define como:
se define como: ![]() .
.
Si para todos los estados ![]() y símbolos de cinta
y símbolos de cinta ![]() ,
, ![]() tiene como máximo un elemento, se dice que la TM es determinista. Si existen transiciones con más de una opción, la TM es no determinista.
tiene como máximo un elemento, se dice que la TM es determinista. Si existen transiciones con más de una opción, la TM es no determinista.
La secuencia de ID de TM deterministas es lineal. Para TM no deterministas, forma un árbol de cálculo . El no determinismo puede pensarse como si la máquina creara réplicas de sí misma que proceden en paralelo. Esta útil analogía será utilizada por nuestro simulador.
A primera vista, podemos pensar que las MT no deterministas son más poderosas que las deterministas debido a la capacidad de “adivinar” el camino correcto. Pero esto no es cierto: un DTM es solo un caso particular de un NDTM, y cualquier NDTM se puede convertir en un DTM. Por lo tanto, tienen el mismo poder computacional.
De hecho, se han propuesto varias variantes de TM: con cinta infinita de dos vías, con varias pistas, sin opción de permanencia, etc. Curiosamente, todas estas variantes exhiben la misma potencia computacional que el modelo básico. Reconocen la misma clase de lenguajes.
En la siguiente sección presentamos una variante muy útil: las TM no deterministas multicinta.
Definición formal: la multicinta TM
Los Multitape TM tienen múltiples cintas de entrada y salida con cabezales independientes. Esta variante no aumenta la potencia computacional del original, pero como veremos puede simplificar la construcción de MTs usando cintas auxiliares.
Una k-tape TM es una tupla de 7 ![]() donde todos los elementos son como en la TM básica, excepto la función de transición que es un mapeo
donde todos los elementos son como en la TM básica, excepto la función de transición que es un mapeo ![]() . Mapea pares de símbolos de lectura de estado a subconjuntos de pares nuevos símbolos de escritura de estados + direcciones.
. Mapea pares de símbolos de lectura de estado a subconjuntos de pares nuevos símbolos de escritura de estados + direcciones.
Por ejemplo, la siguiente TM de 2 cintas calcula la suma de los números almacenados en notación unaria en la primera cinta. La primera cinta contiene factores: secuencias de 1 separados por 0 que representan números naturales. La máquina escribe todos los 1 en la cinta 2, calculando la suma de todos los factores.
Formalmente, deja ![]() donde
donde ![]() se define de la siguiente manera:
se define de la siguiente manera:
- Omitir todos los 0:
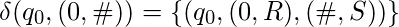
- Copie los 1 a la cinta 2:
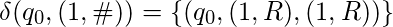
- Detener cuando se alcanza el espacio en blanco:
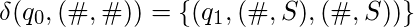
El problema de la detención
Es posible que un TM no se detenga para algunas entradas. Por ejemplo, considere la TM ![]() con
con ![]() .
.
El problema de la detención establece que es indecidible verificar si una TM arbitraria se detendrá en una string de entrada determinada. Este problema tiene profundas implicaciones, porque muestra que hay problemas que no pueden ser calculados por MTs y, si la tesis de Church-Turing es cierta, significa que ningún algoritmo puede resolver estos problemas.
Para un simulador de MT esto es una muy mala noticia, porque implica que el simulador podría entrar en un bucle infinito.
No podemos evitar por completo este problema, pero podemos resolverlo de forma restringida. Considere el caso de una TM no determinista donde hay ramas del árbol de cálculo que entran en un ciclo infinito y crecen para siempre donde otras alcanzan un estado final. En este caso, el simulador debería dejar de aceptar la string de entrada. Pero si recorremos el árbol en un modo de búsqueda en profundidad (DFS), el simulador se atascará cuando entre en una de las ramas infinitas. Para evitar esto, el simulador atravesará el árbol de cálculo a través de la búsqueda en amplitud (BFS). BFS es una estrategia de gráfico transversal que explora todos los hijos de una rama antes de proceder con sus sucesores.
Un simulador de NDTM multicinta en Python
En esta sección presentaremos un simulador para MT no deterministas con múltiples cintas escritas en Python.
El simulador consta de dos clases: una clase Tape y una clase NDTM.
Las instancias de cinta contienen la lista de celdas escaneadas actuales y un índice del encabezado de la cinta, y proporcionan las siguientes operaciones:
- readSymbol(): devuelve el símbolo escaneado por la cabeza, o un espacio en blanco si la cabeza está en la última celda escaneada
- writeSymbol(): reemplaza el símbolo escaneado por la cabeza por otro. Si el encabezado está en las últimas celdas escaneadas, agrega el símbolo al final de la lista de símbolos.
- moveHead(): mueve la cabeza una posición a la izquierda (-1), a la derecha (1) o ninguna posición (0).
- clone(): crea una réplica o copia de la cinta. Esto será muy útil para simular el no determinismo.
Las instancias de NDTM tienen los siguientes atributos:
- los estados inicial y final.
- el estado actual.
- la lista de cintas (objetos de cinta).
- un diccionario de transiciones.
La función de transición se implementa con un diccionario cuyas claves son tuplas (estado, leer_símbolos) y cuyos valores son listas de tuplas (nuevo_estado, movimientos). Por ejemplo, la TM que suma números en notación unaria presentada anteriormente se representará como:
{('q0', ('1', '#')): [('q0', (('1', 'R'), ('1', 'R')))],
('q0', ('0', '#')): [('q0', (('0', 'R'), ('#', 'S')))],
('q0', ('#', '#')): [('q1', (('#', 'S'), ('#', 'S')))]}
Observe cómo la representación de Python se parece mucho a la definición matemática de la función de transición, gracias a las estructuras de datos versátiles de Python como diccionarios, tuplas y listas. Se utiliza una subclase de dict, defaultdict del módulo de colecciones estándar, para aliviar la carga de la inicialización.
Los objetos NDTM contienen métodos para leer la tupla actual de símbolos en las cintas, para agregar, obtener y ejecutar transiciones y para hacer réplicas de la TM actual.
El método principal de NDTM es accepts(). Su argumento es una string de entrada y devuelve un objeto NDTM si alguna rama del árbol de cálculo alcanza el estado de aceptación o Ninguno si ninguna de las ramas lo hace. Atraviesa el árbol de cálculo a través de la búsqueda en amplitud (BFS) para permitir que el cálculo se detenga si alguna rama alcanza el estado de aceptación. BFS utiliza una cola para realizar un seguimiento de las ramas pendientes. Se utiliza una deque de Python del módulo de colecciones para obtener el rendimiento O(1) en las operaciones de la cola. El algoritmo es como sigue:
Add the TM instance to the queue
While queue is not empty:
Fetch the first TM from the queue
If there is no transition for the current state and read symbols:
If the TM is in a final state: return TM
Else:
If the transition is nondeterministic:
Create replicas of the TM and add them to the queue
Execute the transition in the current TM and add it to the queue
Finalmente, la clase NDTM tiene métodos para imprimir la representación de TM como una colección de descripciones instantáneas y para analizar la especificación de TM desde un archivo. Como es habitual, estas instalaciones de entrada/salida son la parte más engorrosa del simulador.
Los archivos de especificación tienen la siguiente sintaxis
% HEADER: mandatory start_state final_state blank number_of_tapes % TRANSITIONS state read_symbols new_state write_symbol, move write_symbol, move ...
Las líneas que comienzan con ‘%’ se consideran comentarios. Por ejemplo, la MT que suma números en notación unaria tiene el siguiente archivo de especificación:
% HEADER q0 q1 # 2 % TRANSITIONS q0 1, # q0 1, R 1, R q0 0, # q0 0, R #, S q0 #, # q1 #, S #, S
Los estados y símbolos pueden ser cualquier string que no contenga espacios en blanco ni comas.
El simulador se puede ejecutar desde una sesión de Python para explorar la configuración de salida. Por ejemplo, si el archivo anterior se guarda con el nombre “2sum.tm”:
Python3
from NDTM import NDTM
tm = NDTM.parse('2sum.tm')
print(tm.accepts('11011101'))
El resultado muestra que el simulador ha producido la suma de los 1 en la cinta #1:
Output : q1: ['1', '1', '0', '1', '1', '1', '0', '1']['#'] q1: ['1', '1', '1', '1', '1', '1']['#']
La salida muestra el contenido de las dos cintas, las posiciones de las cabezas (segunda lista de cada cinta) y el estado final de la MT.
Código fuente del simulador
Excluyendo el código de entrada/salida y los comentarios, el simulador tiene menos de 100 líneas de código. Es un testimonio del poder y la economía de Python. Está orientado a objetos, pero también utiliza construcciones funcionales como listas de comprensión.
Python3
####
# NDTM.py: a nondeterministic Turing Machine Simulator
# Author: David Gil del Rosal (dgilros@yahoo.com)
#### from collections import defaultdict, deque
class Tape:
# Constructor. Sets the blank symbol, the
# string to load and the position of the tape head
def __init__(self, blank, string ='', head = 0):
self.blank = blank
self.loadString(string, head)
# Loads a new string and sets the tape head
def loadString(self, string, head):
self.symbols = list(string)
self.head = head
# Returns the symbol on the current cell, or the blank
# if the head is on the start of the infinite blanks
def readSymbol(self):
if self.head < len(self.symbols):
return self.symbols[self.head]
else:
return self.blank
# Writes a symbol in the current cell, extending
# the list if necessary
def writeSymbol(self, symbol):
if self.head < len(self.symbols):
self.symbols[self.head] = symbol
else:
self.symbols.append(symbol)
# Moves the head left (-1), stay (0) or right (1)
def moveHead(self, direction):
if direction == 'L': inc = -1
elif direction == 'R': inc = 1
else: inc = 0
self.head+= inc
# Creates a new tape with the same attributes than this
def clone(self):
return Tape(self.blank, self.symbols, self.head)
# String representation of the tape
def __str__(self):
return str(self.symbols[:self.head]) + \
str(self.symbols[self.head:])
class NDTM:
# Constructor. Sets the start and final states and
# inits the TM tapes
def __init__(self, start, final, blank ='#', ntapes = 1):
self.start = self.state = start
self.final = final
self.tapes = [Tape(blank) for _ in range(ntapes)]
self.trans = defaultdict(list)
# Puts the TM in the start state and loads an input
# string into the first tape
def restart(self, string):
self.state = self.start
self.tapes[0].loadString(string, 0)
for tape in self.tapes[1:]:
tape.loadString('', 0)
# Returns a tuple with the current symbols read
def readSymbols(self):
return tuple(tape.readSymbol() for tape in self.tapes)
# Add an entry to the transaction table
def addTrans(self, state, read_sym, new_state, moves):
self.trans[(state, read_sym)].append((new_state, moves))
# Returns the transaction that corresponds to the
# current state & read symbols, or None if there is not
def getTrans(self):
key = (self.state, self.readSymbols())
return self.trans[key] if key in self.trans else None
# Executes a transaction updating the state and the
# tapes. Returns the TM object to allow chaining
def execTrans(self, trans):
self.state, moves = trans
for tape, move in zip(self.tapes, moves):
symbol, direction = move
tape.writeSymbol(symbol)
tape.moveHead(direction)
return self
# Returns a copy of the current TM
def clone(self):
tm = NDTM(self.start, self.final)
tm.state = self.state
tm.tapes = [tape.clone() for tape in self.tapes]
tm.trans = self.trans # shallow copy
return tm
# Simulates the TM computation. Returns the TM that
# accepted the input string if any, or None.
def accepts(self, string):
self.restart(string)
queue = deque([self])
while len(queue) > 0:
tm = queue.popleft()
transitions = tm.getTrans()
if transitions is None:
# there are not transactions. Exit
# if the TM is in the final state
if tm.state == tm.final: return tm
else:
# If the transaction is not deterministic
# add replicas of the TM to the queue
for trans in transitions[1:]:
queue.append(tm.clone().execTrans(trans))
# execute the current transition
queue.append(tm.execTrans(transitions[0]))
return None
def __str__(self):
out = ''
for tape in self.tapes:
out+= self.state + ': ' + str(tape) + '\n'
return out
# Simple parser that builds a TM from a text file
@staticmethod
def parse(filename):
tm = None
with open(filename) as file:
for line in file:
spec = line.strip()
if len(spec) == 0 or spec[0] == '%': continue
if tm is None:
start, final, blank, ntapes = spec.split()
ntapes = int(ntapes)
tm = NDTM(start, final, blank, ntapes)
else:
fields = line.split()
state = fields[0]
symbols = tuple(fields[1].split(', '))
new_st = fields[2]
moves = tuple(tuple(m.split(', '))
for m in fields[3:])
tm.addTrans(state, symbols, new_st, moves)
return tm
if __name__ == '__main__':
# Example TM that performs unary complement
tm = NDTM('q0', 'q1', '#')
tm.addTrans('q0', ('0', ), 'q0', (('1', 'R'), ))
tm.addTrans('q0', ('1', ), 'q0', (('0', 'R'), ))
tm.addTrans('q0', ('#', ), 'q1', (('#', 'S'), ))
acc_tm = tm.accepts('11011101')
if acc_tm: print(acc_tm)
else: print('NOT ACCEPTED')
Un ejemplo no trivial
Como ejemplo final, presentamos la especificación de una TM de 3 cintas que reconoce el lenguaje no libre de contexto ![]() .
.
La TM copia de manera no determinista el contenido de la primera mitad de la string en la cinta #2 y la segunda mitad en la cinta #3. Luego, se procede a comprobar si ambas partes coinciden.
% 3-tape NDTM that recognizes L={ ww | w in {0, 1}* }
q0 q4 # 3
% TRANSITIONS
% put left endmarkers on tapes #2 and #3
q0 0, #, # q1 0, S $, R $, R
q0 1, #, # q1 1, S $, R $, R
% first half of string: copy symbols on tape #2
q1 0, #, # q1 0, R 0, R #, S
q1 1, #, # q1 1, R 1, R #, S
% guess second half of string: copy symbols on tape #3
q1 0, #, # q2 0, R #, S 0, R
q1 1, #, # q2 1, R #, S 1, R
q2 0, #, # q2 0, R #, S 0, R
q2 1, #, # q2 1, R #, S 1, R
% reached end of input string: switch to compare state
q2 #, #, # q3 #, S #, L #, L
% compare strings on tapes #2 and #3
q3 #, 0, 0 q3 #, S 0, L 0, L
q3 #, 1, 1 q3 #, S 1, L 1, L
% if both strings are equal switch to final state
q3 #, $, $ q4 #, S $, S $, S
Ejemplo de uso. Guarde el archivo anterior como «3ww.tm» y ejecute el siguiente código:
Python3
from NDTM import NDTM
tm = NDTM.parse('3ww.tm')
print(tm.accepts('11001100'))
La salida producida es la esperada: la TM alcanzó el estado final y el contenido de las dos mitades de la string de entrada está en las cintas #2 y #3.
Output : q4: ['1', '1', '0', '0', '1', '1', '0', '0']['#'] q4: []['$', '1', '1', '0', '0', '#'] q4: []['$', '1', '1', '0', '0', '#']
Un ejercicio interesante es tratar de transformar esta MT en una MT no determinista de una cinta o incluso en una determinista de una cinta. Es perfectamente posible, pero la especificación será mucho más engorrosa. Esta es la utilidad de tener múltiples cintas: no más poder computacional sino mayor simplicidad.