Medidas de centralidad de red en un grafo usando Networkx | Python

Medidas de centralidad nos permite señalar los Nodes más importantes de un gráfico. Esto esencialmente nos ayuda a identificar:

• Nodes influyentes en una Red Social.
• Nodes que difunden información a muchos Nodes
• Nodes en una red de transporte
• Paginas importantes en la Web
• Nodes que evitan que la Red se rompa

En primer lugar, debemos considerar el famoso gráfico social publicado en 1977 llamado gráfico del club de karate de Zachary. Es un gráfico incorporado en Networkx. Todas las medidas de centralidad se demostrarán utilizando este gráfico.

import matplotlib.pyplot as plt
import networkx as nx
  
G = nx.karate_club_graph()
  
plt.figure(figsize =(15, 15))
nx.draw_networkx(g, with_labels = True)

Producción:

 

Las técnicas comúnmente utilizadas para las medidas de centralidad son las siguientes:

Grado de centralidad:

Esto se basa en la suposición de que los Nodes importantes tienen muchas conexiones.

, where is the Degree of node v and N is the set of all nodes of the Graph.

En Networkx,

deg_centrality = nx.degree_centrality(G)
  
# G is the Karate Club Graph
print(deg_centrality)

Producción:

{0: 0.48484848484848486,
 1: 0.2727272727272727,
 2: 0.30303030303030304,
 3: 0.18181818181818182,
 4: 0.09090909090909091,
 5: 0.12121212121212122,
 6: 0.12121212121212122,
 7: 0.12121212121212122,
 8: 0.15151515151515152,
 9: 0.06060606060606061,
 10: 0.09090909090909091,
 11: 0.030303030303030304,
 12: 0.06060606060606061,
 13: 0.15151515151515152,
 14: 0.06060606060606061,
 15: 0.06060606060606061,
 16: 0.06060606060606061,
 17: 0.06060606060606061,
 18: 0.06060606060606061,
 19: 0.09090909090909091,
 20: 0.06060606060606061,
 21: 0.06060606060606061,
 22: 0.06060606060606061,
 23: 0.15151515151515152,
 24: 0.09090909090909091,
 25: 0.09090909090909091,
 26: 0.06060606060606061,
 27: 0.12121212121212122,
 28: 0.09090909090909091,
 29: 0.12121212121212122,
 30: 0.12121212121212122,
 31: 0.18181818181818182,
 32: 0.36363636363636365,
 33: 0.5151515151515151}

Devuelve un diccionario de tamaño igual al número de Nodes en el Gráfico G, donde el i-ésimo elemento es la medida de grado de centralidad del i-ésimo Node. Para gráficos dirigidos, las medidas son diferentes para el grado de entrada y salida. Estos se calculan por:

in_deg_centrality = nx.in_degree_centrality(G)
out_deg_centrality = nx.out_degree_centrality(G)

donde g es un gráfico dirigido.

Cercanía Centralidad :

Esto se basa en la suposición de que los Nodes importantes están cerca de otros Nodes. Se calcula como la suma de las longitudes de los caminos desde el Node dado hasta todos los demás Nodes. Pero para un Node que no puede alcanzar a todos los demás Nodes, la centralidad de cercanía se mide usando la siguiente fórmula:
donde, R(v) es el conjunto de todos los Nodes que v puede alcanzar.

close_centrality = nx.closeness_centrality(G)
  
# G is the Karate Social Graph
print(close_centrality)

Producción:

{0: 0.5689655172413793,
 1: 0.4852941176470588,
 2: 0.559322033898305,
 3: 0.4647887323943662,
 4: 0.3793103448275862,
 5: 0.38372093023255816,
 6: 0.38372093023255816,
 7: 0.44,
 8: 0.515625,
 9: 0.4342105263157895,
 10: 0.3793103448275862,
 11: 0.36666666666666664,
 12: 0.3707865168539326,
 13: 0.515625,
 14: 0.3707865168539326,
 15: 0.3707865168539326,
 16: 0.28448275862068967,
 17: 0.375,
 18: 0.3707865168539326,
 19: 0.5,
 20: 0.3707865168539326,
 21: 0.375,
 22: 0.3707865168539326,
 23: 0.39285714285714285,
 24: 0.375,
 25: 0.375,
 26: 0.3626373626373626,
 27: 0.4583333333333333,
 28: 0.4520547945205479,
 29: 0.38372093023255816,
 30: 0.4583333333333333,
 31: 0.5409836065573771,
 32: 0.515625,
 33: 0.55}

Centralidad de intermediación:

Asume que los Nodes importantes conectan otros Nodes. La fórmula para calcular la centralidad de intermediación es la siguiente:
donde es el número de caminos más cortos entre los Nodes s y t. es el número de caminos más cortos entre los Nodes s y t que pasan por v.
Podemos o no incluir el Node v en el cálculo.

Para Grafos con un gran número de Nodes, el valor de centralidad de intermediación es muy alto. Entonces, podemos normalizar el valor dividiendo por el número de pares de Nodes (excluyendo el Node actual). Para gráficos dirigidos, el número de pares de Nodes es (|N|-1)*(|N|-2), mientras que para gráficos no dirigidos, el número de pares de Nodes es (1/2)*(|N|-1)*(|N|-2).

bet_centrality = nx.betweenness_centrality(G, normalized = True, 
                                              endpoints = False)
  
# G is the Karate Social Graph, parameters normalized
# and endpoints ensure whether we normalize the value
# and consider the endpoints respectively.
print(bet_centrality)

Producción:

{0: 0.43763528138528146,
 1: 0.053936688311688304,
 2: 0.14365680615680618,
 3: 0.011909271284271283,
 4: 0.0006313131313131313,
 5: 0.02998737373737374,
 6: 0.029987373737373736,
 7: 0.0,
 8: 0.05592682780182781,
 9: 0.0008477633477633478,
 10: 0.0006313131313131313,
 11: 0.0,
 12: 0.0,
 13: 0.04586339586339586,
 14: 0.0,
 15: 0.0,
 16: 0.0,
 17: 0.0,
 18: 0.0,
 19: 0.03247504810004811,
 20: 0.0,
 21: 0.0,
 22: 0.0,
 23: 0.017613636363636363,
 24: 0.0022095959595959595,
 25: 0.0038404882154882154,
 26: 0.0,
 27: 0.02233345358345358,
 28: 0.0017947330447330447,
 29: 0.0029220779220779218,
 30: 0.014411976911976909,
 31: 0.13827561327561325,
 32: 0.145247113997114,
 33: 0.30407497594997596}

Rango de página :

Page Rank Algorithm fue desarrollado por los fundadores de Google para medir la importancia de las páginas web a partir de la estructura de la red de hipervínculos. Page Rank asigna una puntuación de importancia a cada Node. Los Nodes importantes son aquellos con muchos enlaces desde páginas importantes. Funciona principalmente para redes dirigidas.

n -> Number of nodes
k -> Number of steps

All nodes have a Page Rank of 1/n
Repeat k times : 
    For node u pointing to node v, add Page Rank of u 
    divided by out degree of u to the Page Rank of v

Para comprender el Page Rank, consideraremos el siguiente gráfico:

Let k = 2

Initially,
A -> 1/5
B -> 1/5
C -> 1/5
D -> 1/5
E -> 1/5

After first iteration,
A -> 1/15+1/5 = 4/15
B -> 1/5+1/5 = 2/5
C -> 1/10+1/15 = 1/6
D -> 1/10
E -> 1/15

After second iteration,
A -> 1/30+1/15 = 1/10
B -> 4/15+1/6 = 13/30
C -> 1/5+1/30 = 7/30
D -> 1/5
E -> 1/30

So, after 2 iterations, Page Rank is as follows:
B > C > D > A > E

Page Rank de un Node en el paso k es la probabilidad de que un caminante aleatorio aterrice en el Node después de dar k pasos.
Ahora, consideremos la siguiente red,

para un paseo aleatorio donde k tiende a infinito, eventualmente irá a F o G y se atascará allí. Por lo tanto, Page Rank para F = 1/2, G = 1/2, el resto de los Nodes tendrán Page Rank de 0. Esto se resuelve introduciendo un ‘parámetro de amortiguación’ .

Each node has a Page Rank of 1/n
Start on a Random Node
Repeat k times:
     With probability 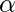, choose an outgoing edge at random and follow it to the next node. 
     With probability , choose a random node and go to it.

El valor de alfa generalmente se establece entre 0,8 y 0,9.

pr = nx.pagerank(G, alpha = 0.8)
  
# G is the Karate Social Graph
print(pr)

Producción:

{0: 0.09456117898156402,
 1: 0.05152334607950815,
 2: 0.05510962827358582,
 3: 0.03520686871052657,
 4: 0.022556530085318473,
 5: 0.02965434765152121,
 6: 0.02965434765152121,
 7: 0.02429306613631948,
 8: 0.029203590410895465,
 9: 0.014918270732782356,
 10: 0.022556530085318473,
 11: 0.010610337618460166,
 12: 0.015304584795945321,
 13: 0.028920243421725694,
 14: 0.015180200879547068,
 15: 0.015180200879547068,
 16: 0.01774436545128434,
 17: 0.01519007845263465,
 18: 0.015180200879547068,
 19: 0.019817255738040863,
 20: 0.015180200879547068,
 21: 0.01519007845263465,
 22: 0.015180200879547068,
 23: 0.03138523208020211,
 24: 0.021678994504154954,
 25: 0.021582293035938838,
 26: 0.015815184517974507,
 27: 0.02572094617382946,
 28: 0.019815535386497624,
 29: 0.026528036905982717,
 30: 0.024432622368453834,
 31: 0.03672846196415318,
 32: 0.07006405452640968,
 33: 0.09833298540908077}

Estas son las diversas medidas de Centralidad en una Red. Hay otros métodos como Load Centrality, Katz Centrality, Percolation Centrality, etc.