Python – Distribución Binomial

La distribución binomial es una distribución de probabilidad que resume la probabilidad de que una variable tome uno de dos valores independientes bajo un conjunto dado de parámetros. La distribución se obtiene realizando varios ensayos de Bernoulli .

Se supone que un ensayo de Bernoulli cumple con cada uno de estos criterios:

• Debe haber sólo 2 resultados posibles.
• Cada resultado tiene una probabilidad fija de ocurrir. Un éxito tiene la probabilidad de p, y un fracaso tiene la probabilidad de 1 – p.
• Cada ensayo es completamente independiente de todos los demás.

La variable aleatoria binomial representa el número de éxitos ( r ) en n ensayos independientes sucesivos de un experimento de Bernoulli.

La probabilidad de lograr r éxito y nr fracaso es:

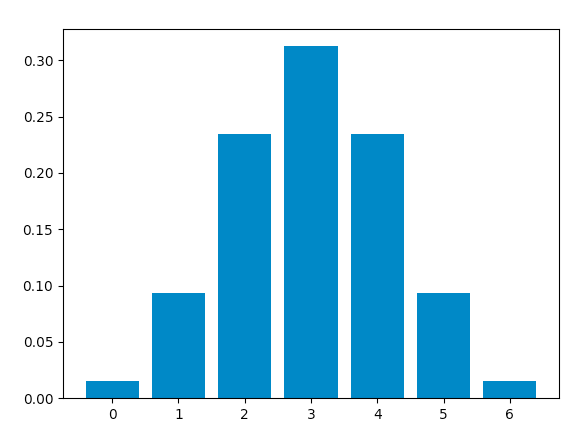
Considere un experimento aleatorio de lanzar una moneda sesgada 6 veces donde la probabilidad de obtener una cara es 0.6 . Si ‘sacar cara’ se considera ‘ éxito’ , la tabla de distribución binomial contendrá la probabilidad de r éxitos para cada valor posible de r.

Esta distribución tiene una media igual a np y una varianza de np(1-p) . 

Usando Python para obtener la distribución:
Ahora, usaremos Python para analizar la distribución (usando SciPy ) y trazar el gráfico (usando Matplotlib ).
Módulos requeridos:

• SciPy:
  SciPy es una biblioteca Python de código abierto, utilizada en matemáticas, ingeniería, informática científica y técnica.

  Instalación :

  pip install scipy
  

• Matplotlib:
  Matplotlib es una completa biblioteca de Python para trazar gráficos y visualizaciones estáticas e interactivas. 

  Instalación :

  pip install matplotlib
  

El módulo scipy.stats contiene varias funciones para cálculos y pruebas estadísticas. La función stats() del módulo scipy.stats.binom se puede usar para calcular una distribución binomial usando los valores de n y p .

Sintaxis : scipy.stats.binom.stats(n, p)

Devuelve una tupla que contiene la media y la varianza de la distribución en ese orden.

La función scipy.stats.binom.pmf() se usa para obtener la función de masa de probabilidad para un cierto valor de r, n y p. Podemos obtener la distribución pasando todos los valores posibles de r(0 a n).

Sintaxis : scipy.stats.binom.pmf(r, n, p)

Cálculo de la tabla de distribución:

Acercarse :

• Defina n y p .
• Defina una lista de valores de r de 0 a n.
• Obtenga la media y la varianza .
• Para cada r, calcule la pmf y guárdela en una lista.

Código:

from scipy.stats import binom
# setting the values
# of n and p
n = 6
p = 0.6
# defining the list of r values
r_values = list(range(n + 1))
# obtaining the mean and variance 
mean, var = binom.stats(n, p)
# list of pmf values
dist = [binom.pmf(r, n, p) for r in r_values ]
# printing the table
print("r\tp(r)")
for i in range(n + 1):
    print(str(r_values[i]) + "\t" + str(dist[i]))
# printing mean and variance
print("mean = "+str(mean))
print("variance = "+str(var))

Producción :

r    p(r)
0    0.004096000000000002
1    0.03686400000000005
2    0.13824000000000003
3    0.2764800000000001
4    0.31104
5    0.18662400000000007
6    0.04665599999999999
mean = 3.5999999999999996
variance = 1.44

Código: Trazar el gráfico usando la función matplotlib.pyplot.bar() para trazar barras verticales.

from scipy.stats import binom
import matplotlib.pyplot as plt
# setting the values
# of n and p
n = 6
p = 0.6
# defining list of r values
r_values = list(range(n + 1))
# list of pmf values
dist = [binom.pmf(r, n, p) for r in r_values ]
# plotting the graph 
plt.bar(r_values, dist)
plt.show()

Producción :