Prerrequisito: Introducción a las Redes Sociales , Modelo Erdos-Renyi
El modelo Erdos Renyi se utiliza para crear redes o gráficos aleatorios en las redes sociales. En el modelo Erdos Reny, cada borde tiene una probabilidad fija de estar presente y estar ausente independientemente de los bordes de una red.
Implementando una Red Social usando el modelo Erdos-Renyi:
Paso 1) Importe los módulos necesarios como networkx , matplotlib.pyplot y el módulo random.
Python3
# Import Required modules import networkx as nx import matplotlib.pyplot as plt import random
Paso 2) Cree un gráfico de distribución para el modelo.
Python3
# Distribution graph for Erdos_Renyi model
def distribution_graph(g):
print(nx.degree(g))
all_node_degree = list(dict((nx.degree(g))).values())
unique_degree = list(set(all_node_degree))
unique_degree.sort()
nodes_with_degree = []
for i in unique_degree:
nodes_with_degree.append(all_node_degree.count(i))
plt.plot(unique_degree, nodes_with_degree)
plt.xlabel("Degrees")
plt.ylabel("No. of nodes")
plt.title("Degree distribution")
plt.show()
Paso 3) Tome N , es decir, el número de Nodes del usuario.
Python3
# Take N number of nodes as input
print("Enter number of nodes")
N = int(input())
Paso 4) Ahora tome P , es decir, la probabilidad del usuario para los bordes.
Python3
# Take P probability value for edges
print("Enter value of probability of every node")
P = float(input())
Paso 5) Crea un gráfico con N Nodes sin bordes.
Python3
# Create an empty graph object g = nx.Graph() # Adding nodes g.add_nodes_from(range(1, N + 1))
Paso 6) Agregue los bordes al gráfico al azar, tome un par de Nodes y obtenga un número aleatorio R . Si R<P (probabilidad), agregue una ventaja. Repita los pasos 5 y 6 para todos los pares de Nodes posibles y luego visualice toda la red social (gráfico) formada.
Python3
# Add edges to the graph randomly. for i in g.nodes(): for j in g.nodes(): if (i < j): # Take random number R. R = random.random() # Check if R<P add the edge # to the graph else ignore. if (R < P): g.add_edge(i, j) pos = nx.circular_layout(g) # Display the social network nx.draw(g, pos, with_labels=1) plt.show()
Paso 7) Mostrar los Nodes de conexión.
Python3
# Display connection between nodes distribution_graph(g)
A continuación se muestra el programa completo del enfoque paso a paso anterior:
Python3
# Implementation of Erdos-Renyi Model on a Social Network
# Import Required modules
import networkx as nx
import matplotlib.pyplot as plt
import random
# Distribution graph for Erdos_Renyi model
def distribution_graph(g):
print(nx.degree(g))
all_node_degree = list(dict((nx.degree(g))).values())
unique_degree = list(set(all_node_degree))
unique_degree.sort()
nodes_with_degree = []
for i in unique_degree:
nodes_with_degree.append(all_node_degree.count(i))
plt.plot(unique_degree, nodes_with_degree)
plt.xlabel("Degrees")
plt.ylabel("No. of nodes")
plt.title("Degree distribution")
plt.show()
# Take N number of nodes from user
print("Enter number of nodes")
N = int(input())
# Take P probability value for edges
print("Enter value of probability of every node")
P = float(input())
# Create an empty graph object
g = nx.Graph()
# Adding nodes
g.add_nodes_from(range(1, N + 1))
# Add edges to the graph randomly.
for i in g.nodes():
for j in g.nodes():
if (i < j):
# Take random number R.
R = random.random()
# Check if R<P add the edge to the graph else ignore.
if (R < P):
g.add_edge(i, j)
pos = nx.circular_layout(g)
# Display the social network
nx.draw(g, pos, with_labels=1)
plt.show()
# Display connection between nodes
distribution_graph(g)
Producción:
Ingrese el número de Nodes
10
Ingrese el valor de probabilidad de cada Node
0.4
[(1, 5), (2, 3), (3, 4), (4, 2), (5, 3), (6, 5), (7, 4), (8, 2), (9, 2), (10, 2)]
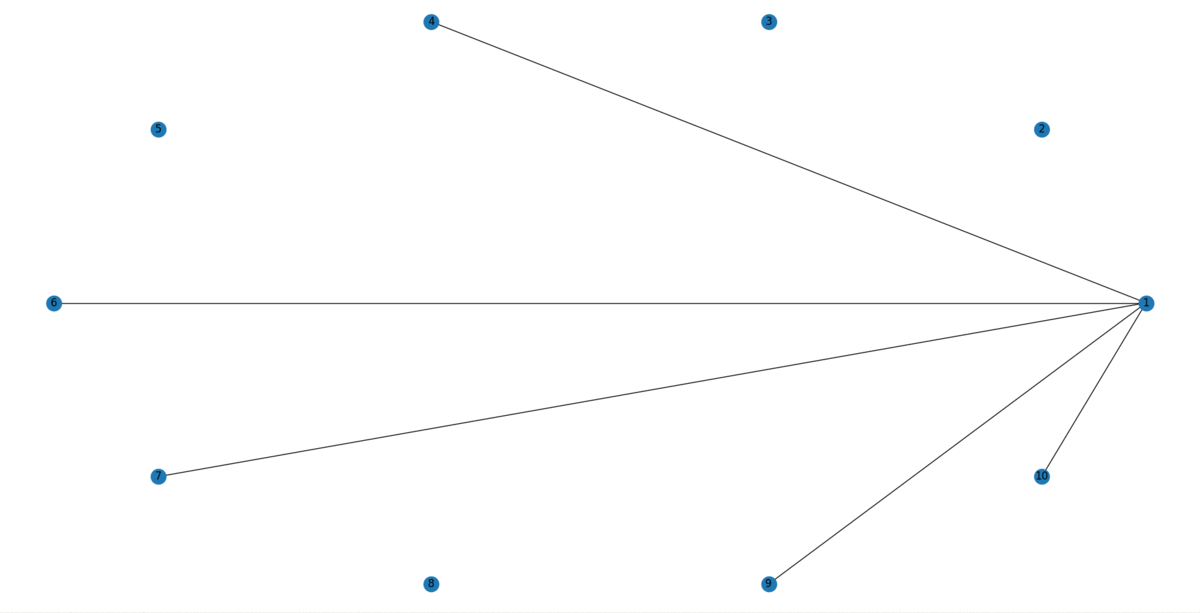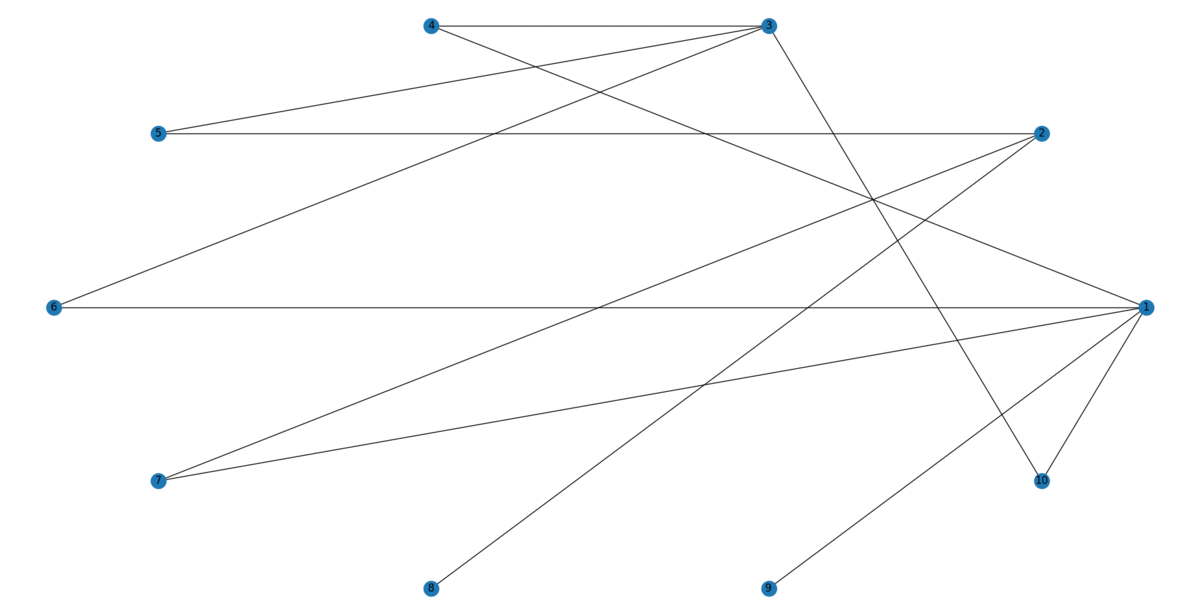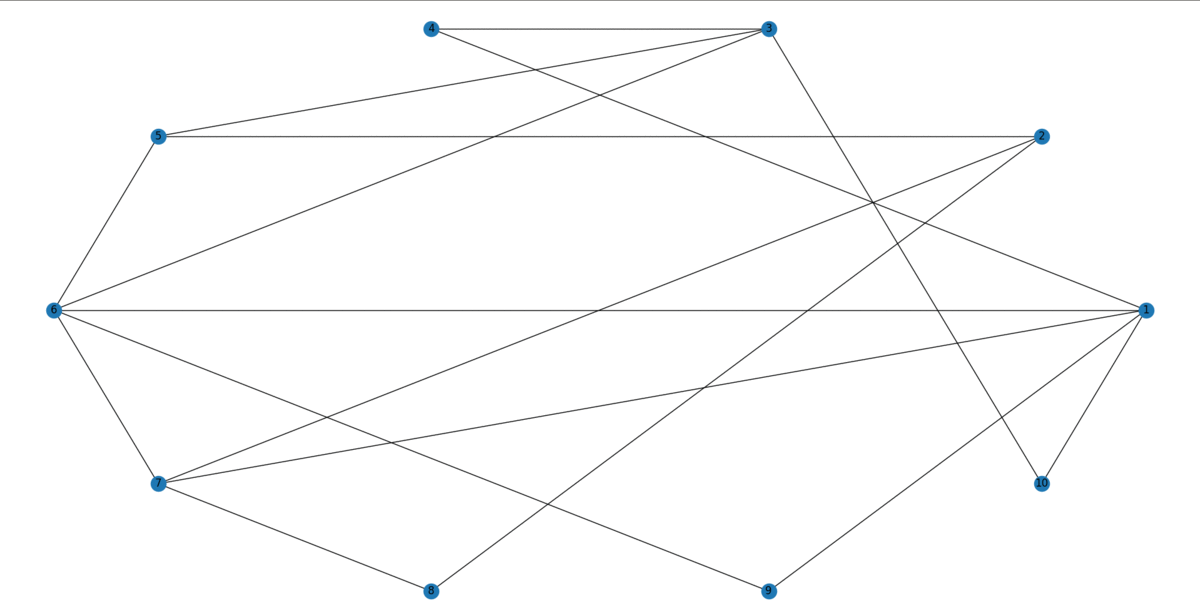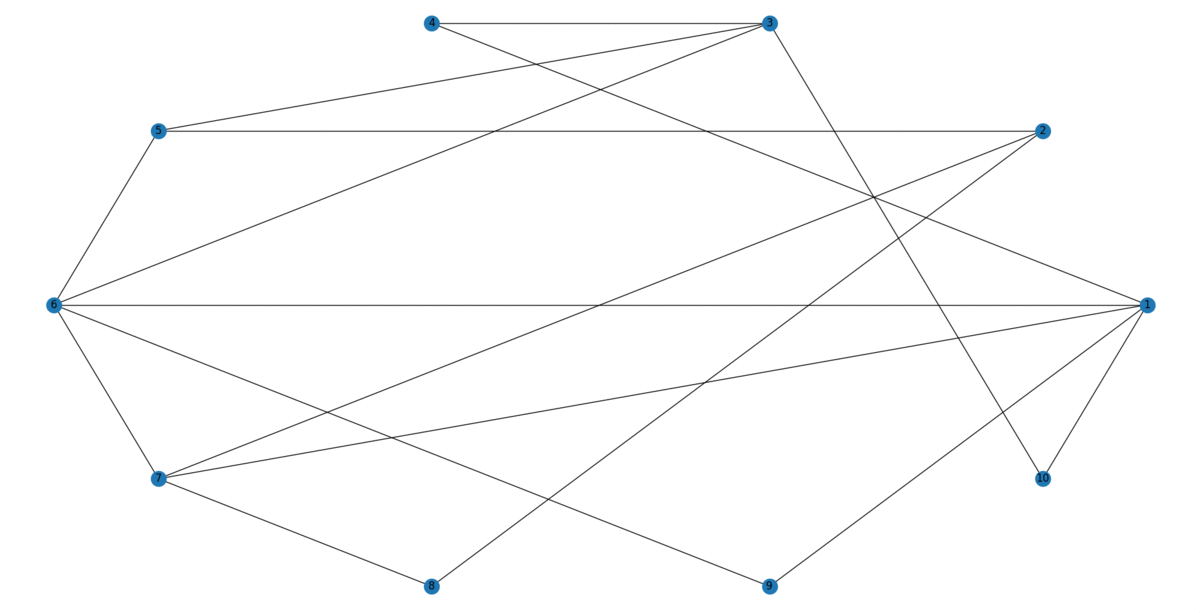
Agregar bordes al azar en un gráfico
Gráfico de distribución de grados de la implementación del modelo Erdos-Renyi en el programa anterior :

Publicación traducida automáticamente
Artículo escrito por sankalpsharma424 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA