Un regresor Ridge es básicamente una versión regularizada de un regresor lineal. es decir, a la función de costo original del regresor lineal le agregamos un término regularizado que obliga al algoritmo de aprendizaje a ajustarse a los datos y ayuda a mantener los pesos lo más bajos posible. El término regularizado tiene el parámetro ‘alfa’ que controla la regularización del modelo, es decir, ayuda a reducir la varianza de las estimaciones.
Función de Costo para Ridge Regressor.
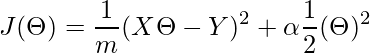
Aquí,
el primer término es la función de costo de nuestra regresión lineal básica y el segundo término es nuestro nuevo término de pesos regularizados que usa la norma L2 para ajustar los datos. Si el ‘alfa’ es cero, el modelo es el mismo que la regresión lineal y el valor ‘alfa’ más grande especifica una regularización más fuerte.
Nota: Antes de usar el regresor de Ridge, es necesario escalar las entradas, porque este modelo es sensible al escalado de las entradas. Por lo tanto, realizar el escalado a través de StandardScalar de sklearn será beneficioso.
Código: código de Python para implementar Ridge Regressor.
Python3
# importing libraries
from sklearn.linear_model import Ridge
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler
# loading boston dataset
boston = load_boston()
X = boston.data[:, :13]
y = boston.target
print ("Boston dataset keys : \n", boston.keys())
print ("\nBoston data : \n", boston.data)
# scaling the inputs
scaler = StandardScaler()
scaled_X = scaler.fit_transform(X)
# Train Test split will be used for both models
X_train, X_test, y_train, y_test = train_test_split(scaled_X, y,
test_size = 0.3)
# training model with 0.5 alpha value
model = Ridge(alpha = 0.5, normalize = False, tol = 0.001, \
solver ='auto', random_state = 42)
model.fit(X_train, y_train)
# predicting the y_test
y_pred = model.predict(X_test)
# finding score for our model
score = model.score(X_test, y_test)
print("\n\nModel score : ", score)
Producción :
Boston dataset keys : dict_keys(['feature_names', 'DESCR', 'data', 'target']) Boston data : [[6.3200e-03 1.8000e+01 2.3100e+00 ... 1.5300e+01 3.9690e+02 4.9800e+00] [2.7310e-02 0.0000e+00 7.0700e+00 ... 1.7800e+01 3.9690e+02 9.1400e+00] [2.7290e-02 0.0000e+00 7.0700e+00 ... 1.7800e+01 3.9283e+02 4.0300e+00] ... [6.0760e-02 0.0000e+00 1.1930e+01 ... 2.1000e+01 3.9690e+02 5.6400e+00] [1.0959e-01 0.0000e+00 1.1930e+01 ... 2.1000e+01 3.9345e+02 6.4800e+00] [4.7410e-02 0.0000e+00 1.1930e+01 ... 2.1000e+01 3.9690e+02 7.8800e+00]] Model score : 0.6819292026260749
Una versión más nueva de RidgeCV viene con validación cruzada incorporada para un alfa, por lo que definitivamente es mejor. Solo pase la array de algunos valores de rango alfa y automáticamente elegirá el valor óptimo para ‘alfa’.
Nota: ‘tol’ es el parámetro que mide la caída de pérdida y asegura que el modelo se detenga en esa posición de valor proporcionada o se detenga en (valor mínimo global).
Publicación traducida automáticamente
Artículo escrito por ankushkuwar05 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA