Python: polinomios de Legendre usando la relación de recursividad

Los polinomios de Legendre son un tipo de polinomios ortogonales que ocurren a menudo en ciencia e ingeniería. Por lo tanto, su generación es crucial para esos campos. Hay diferentes formas de evaluar un polinomio de Legendre, usando funciones generadoras, fórmula de Rodrigues, relación de recurrencia, ortogonalización de Gram-Schmidt, etc. Uno de los
métodos más fáciles y también uno de los más precisos es usar la relación de recurrencia.

Aquí usamos la relación de recurrencia de Bonnet de los polinomios legendarios, es decir, –

Se puede implementar usando Python procediendo de la siguiente manera:

Definimos los polinomios de Legendre como una función llamada P(n, x), donde n se llama el orden del polinomio yx es el punto de evaluación. Los casos base son si n es 0, entonces el valor del polinomio es siempre 1 y es x cuando el orden es 1. Estos son los valores iniciales necesarios para la relación de recurrencia.
Para otros valores de n, la función se define recursivamente, directamente a partir de la recurrencia de Bonnet. Por lo tanto, P(n, x) devuelve valores del polinomio de Legendre, por método de recursión (una función efectivamente definida con otros casos base de la misma función).

A continuación se muestra la implementación de Python:

# Legendre polynomial
def P(n, x): 
    if(n == 0):
        return 1 # P0 = 1
    elif(n == 1):
        return x # P1 = x
    else:
        return (((2 * n)-1)*x * P(n-1, x)-(n-1)*P(n-2, x))/float(n)
  
# Suppose, we want to find the value of 
# 3rd order legendre polynomial at x = 5
# We can display the value by--
  
# Driver program
n = 3
X = 5
print("The value of the polynomial at given point is:", P(n, X))

The value of the polynomial at given point is: 305.0

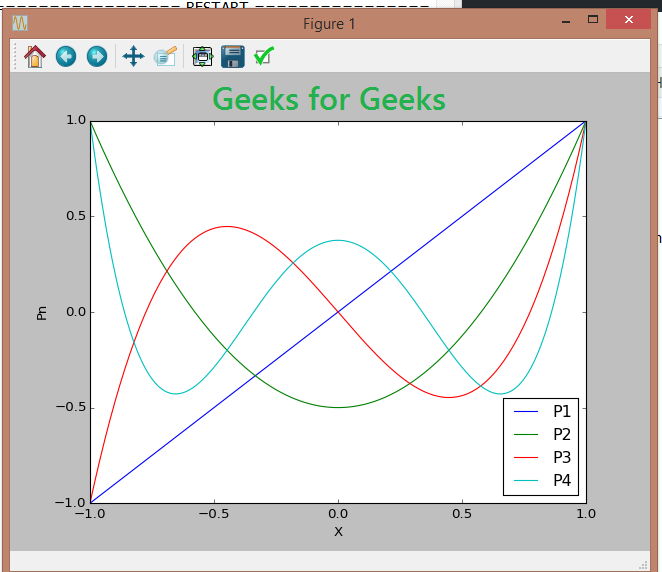
Ahora también podemos trazar los polinomios de Legendre (digamos desde el primer orden hasta el cuarto orden) usando matplotlib.

import matplotlib
  
# This is for use in webbrowser, can be ignored.
matplotlib.use('Agg') 
  
import matplotlib.pyplot as plt
import numpy as np
  
# Creating an array of x values
x = np.linspace(-1, 1, 200) 
  
# for which polynomial values are evaluated and plotted
for i in range(1, 5):
  
    # Labelling according to order
    plt.plot(x, P(i, x), label ="P"+str(i)) 
  
plt.legend(loc ="best")
plt.xlabel("X")
plt.ylabel("Pn")
plt.show()