Uno de los conceptos muy significativos y útiles para simplificar la expresión de salida usando K-Map es el concepto de «No me importa». Las condiciones “No importa” nos permiten reemplazar la celda vacía de un K-Map para formar una agrupación de las variables mayor que la de formar grupos sin no importa. Mientras formamos grupos de celdas, podemos considerar una celda «No me importa» como 1 o 0 o también podemos ignorar esa celda. Por lo tanto, la condición de “No me importa” puede ayudarnos a formar un grupo más grande de células.
Una celda No importa se puede representar con una cruz (X) o menos (-) o phi (Φ) en K-Maps que representan una combinación no válida. Por ejemplo, en el sistema de códigos Excess-3, los estados 0000, 0001, 0010, 1101, 1110 y 1111 no son válidos o no están especificados. Estos estados se llaman no me importa.
Una función estándar de SOP que no tiene interés se puede convertir en una expresión de POS si se mantiene tal como está y se escriben los términos mínimos que faltan en el formulario de SOP como términos máximos del formulario de POS. De manera similar, una función POS que no tiene interés se puede convertir a formato SOP manteniendo los «no importa» tal como están y escribiendo los términos máximos faltantes de la expresión POS como los términos mínimos de la expresión SOP.
Ejemplo-1:
Minimice la siguiente función en forma mínima SOP usando K-Maps:
f = m(1, 5, 6, 11, 12, 13, 14) + d(4)
Explicación:
El mapa K de SOP para la expresión dada es:
Por lo tanto, SOP mínimo es,
f = BC' + BCD' + A'C'D + AB'CD
Ejemplo-2:
Minimice la siguiente función en forma mínima de POS usando K-Maps:
F(A, B, C, D) = m(0, 1, 2, 3, 4, 5) + d(10, 11, 12, 13, 14, 15)
Explicación:
Escribiendo la expresión dada en forma POS:
F(A, B, C, D) = M(6, 7, 8, 9) + d(12, 13, 14, 15)
El K-map POS para la expresión dada es:
Por lo tanto, POS mínimo es,
F = (A'+ C)(B' + C')
Ejemplo-3:
Minimice la siguiente función en forma mínima SOP usando K-Maps:
F(A, B, C, D) = m(1, 2, 6, 7, 8, 13, 14, 15) + d(0 , 3, 5, 12)
Explicación:
El mapa K de SOP para la expresión dada es:
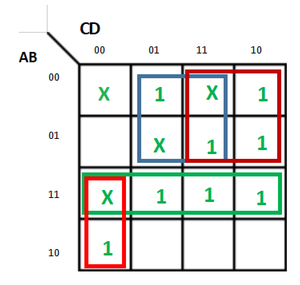
Por lo tanto,
f = AC'D' + A'D + A'C + AB
Importancia de las condiciones de «No importa»: Las condiciones de «No importa»
tienen la siguiente importancia en el diseño de los circuitos digitales:
- Simplificación de la salida:
estas condiciones indican entradas que no son válidas para un circuito digital determinado. Por lo tanto, pueden usarse para simplificar aún más la expresión de salida booleana de un circuito digital.
- Reducción del número de puertas requeridas:
la simplificación de la expresión reduce el número de puertas que se utilizarán para implementar la expresión dada. Por lo tanto, no le importa que el diseño del circuito digital sea más económico.
- Consumo de energía reducido:
al agrupar los términos largos con no importa, se reduce el cambio de estado. Esto disminuye el espacio de memoria que se requiere para representar un circuito digital determinado, lo que a su vez da como resultado un menor consumo de energía.
- Representar estados no válidos en convertidores de código:
se utilizan en convertidores de código. Por ejemplo: en el diseño del convertidor de código BCD a XS-3 de 4 bits, las combinaciones de entrada 1010, 1011, 1100, 1101, 1110 y 1111 no importan.
- Prevención de Riesgos en Circuitos Digitales:
No importa también previene riesgos en sistemas digitales.
Publicación traducida automáticamente
Artículo escrito por vaishnavtannu y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

