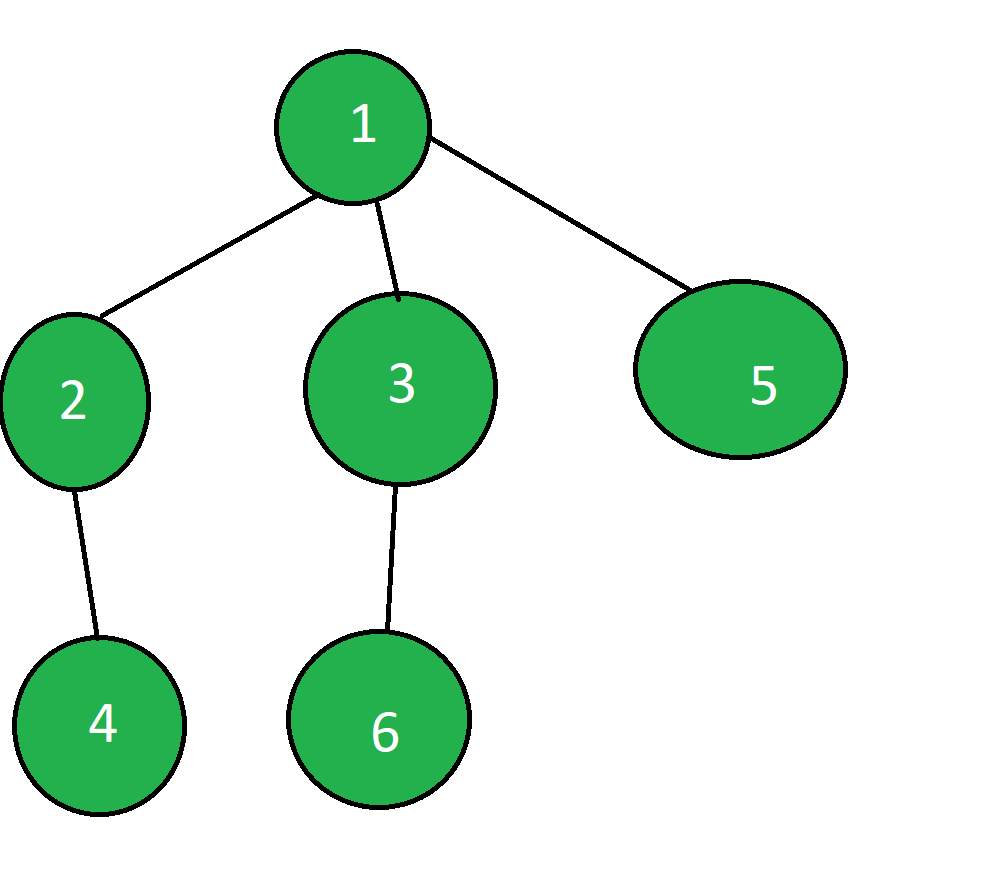
Dado un grafo no dirigido y dos vértices X e Y , nuestra tarea es verificar si el vértice X se encuentra en el subgrafo del vértice Y.
Ejemplos:
Entrada: X = 2, Y = 3
Salida: No
Explicación:
El subgráfico de un vértice Y = 3 es un conjunto de todos los vértices que se encuentran debajo de Y y son accesibles por Y. Aquí el subgráfico de 3 contiene {6} no 2.
Entrada: X = 6, Y = 1
Salida: Sí
Explicación:
El subgráfico de 1 contiene {2, 3, 4, 5, 6} por lo que 6 se encuentra en el subgráfico de 1.
Enfoque: la idea es utilizar la búsqueda en profundidad primero (DFS) . Inicialice dos arrays de entrada y salida para mantener la hora de inicio de atravesar un vértice y la hora de finalización para marcar hasta que se atraviese el vértice. Si el tiempo de inicio del segundo vértice es menor que el tiempo de inicio del primer vértice y el tiempo de finalización del primer vértice es menor que el del segundo vértice, devuelve verdadero; de lo contrario, devuelve falso.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ implementation to check if vertex X
// lies in subgraph of vertex Y
// for the given graph
#include <bits/stdc++.h>
using namespace std;
int cnt = 1;
// Function ot perform dfs
void dfs(vector<int> v[], int in[],
int out[], int visited[], int i)
{
// Mark visited of vertex i
visited[i] = 1;
// Update starting time
// of vertex i
in[i] = cnt;
// Increment the cnt
cnt++;
for (auto x : v[i]) {
// Check if not visited
// call dfs from x
if (!visited[x])
dfs(v, in, out, visited, x);
}
// Update ending time
// of vertex i
out[i] = cnt;
// Increment the cnt
cnt++;
}
// Function to add edges in graph
void addedge(vector<int> v[], int x, int y)
{
v[x].push_back(y);
v[y].push_back(x);
}
// Function to check if vertex X
// lies in subgraph of vertex Y
// for the given graph
bool is_subtree(vector<int> v[], int n,
int m, int x, int y)
{
// Arrays for starting time,
// ending time and to check
// for visited respectively
int in[n + 1], out[n + 1], visited[n + 1];
// Mark all vertices starting time,
// ending time and visited as zero
for (int i = 1; i <= n; i++) {
in[i] = 0;
out[i] = 0;
visited[i] = 0;
}
// Check if y comes before x
// and leaves after x then x lies
// in the subgraph of y
// call dfs from any vertex,
// here we have called from 1
dfs(v, in, out, visited, 1);
if (in[y] < in[x] && out[y] > out[x])
return true;
else
return false;
}
// Driver code
int main()
{
// n number of vertices
// m number of edges
int n = 6, m = 5;
// Create a graph given
// in the above diagram
vector<int> v[n + 1];
addedge(v, 1, 2);
addedge(v, 1, 3);
addedge(v, 2, 4);
addedge(v, 1, 5);
addedge(v, 3, 6);
int x = 6, y = 1;
if (is_subtree(v, n, m, x, y))
cout << "Yes";
else
cout << "No";
return 0;
}
Java
// Java implementation to check if vertex X
// lies in subgraph of vertex Y
// for the given graph
import java.util.*;
class GFG{
static int cnt = 1;
// Function ot perform dfs
static void dfs(Vector<Integer> v[], int in[],
int out[], int visited[], int i)
{
// Mark visited of vertex i
visited[i] = 1;
// Update starting time
// of vertex i
in[i] = cnt;
// Increment the cnt
cnt++;
for(int x : v[i])
{
// Check if not visited
// call dfs from x
if (visited[x] == 0)
dfs(v, in, out, visited, x);
}
// Update ending time
// of vertex i
out[i] = cnt;
// Increment the cnt
cnt++;
}
// Function to add edges in graph
static void addedge(Vector<Integer> v[],
int x, int y)
{
v[x].add(y);
v[y].add(x);
}
// Function to check if vertex X
// lies in subgraph of vertex Y
// for the given graph
static boolean is_subtree(Vector<Integer> v[],
int n, int m, int x,
int y)
{
// Arrays for starting time,
// ending time and to check
// for visited respectively
int []in = new int[n + 1];
int []out = new int[n + 1];
int []visited = new int[n + 1];
// Mark all vertices starting time,
// ending time and visited as zero
for(int i = 1; i <= n; i++)
{
in[i] = 0;
out[i] = 0;
visited[i] = 0;
}
// Check if y comes before x
// and leaves after x then x lies
// in the subgraph of y
// call dfs from any vertex,
// here we have called from 1
dfs(v, in, out, visited, 1);
if (in[y] < in[x] && out[y] > out[x])
return true;
else
return false;
}
// Driver code
public static void main(String[] args)
{
// n number of vertices
// m number of edges
int n = 6, m = 5;
// Create a graph given
// in the above diagram
@SuppressWarnings("unchecked")
Vector<Integer> []v = new Vector[n + 1];
for(int i = 0; i < v.length; i++)
v[i] = new Vector<Integer>();
addedge(v, 1, 2);
addedge(v, 1, 3);
addedge(v, 2, 4);
addedge(v, 1, 5);
addedge(v, 3, 6);
int x = 6, y = 1;
if (is_subtree(v, n, m, x, y))
System.out.print("Yes");
else
System.out.print("No");
}
}
// This code is contributed by PrinciRaj1992
Python3
# Python3 implementation to check if
# vertex X lies in subgraph of
# vertex Y for the given graph
cnt = 1
# Function to perform dfs
def dfs(v, in_, out, visited, i):
global cnt
# Mark visited of vertex i
visited[i] = 1
# Update starting time
# of vertex i
in_[i] = cnt
# Increment the cnt
cnt += 1
# Check if not visited
# call dfs from x
for x in v[i]:
if not visited[x]:
dfs(v, in_, out, visited, x)
# Update ending time
# of vertex i
out[i] = cnt
# Increment the cnt
cnt += 1
# Function to add edges in graph
def addedge(v, x, y):
v[x].append(y)
v[y].append(x)
# Function to check if vertex X
# lies in subgraph of vertex Y
# for the given graph
def is_subtree(v, n, m, x, y):
# Arrays for starting time,
# ending time and to check
# for visited respectively
# Mark all vertices starting time,
# ending time and visited as zero
in_ = [0] * (n + 1)
out = [0] * (n + 1)
visited = [0] * (n + 1)
# Check if y comes before x
# and leaves after x then x lies
# in the subgraph of y
# call dfs from any vertex,
# here we have called from 1
dfs(v, in_, out, visited, 1)
if in_[y] < in_[x] and out[y] > out[x]:
return True
else:
return False
# Driver code
# n number of vertices
# m number of edges
n, m = 6, 5
# Create a graph given
# in the above diagram
v = []
for i in range(n + 1):
v.append([])
addedge(v, 1, 2)
addedge(v, 1, 3)
addedge(v, 2, 4)
addedge(v, 1, 5)
addedge(v, 3, 6)
x, y = 6, 1
if is_subtree(v, n, m, x, y):
print("Yes")
else:
print("No")
# This code is contributed by Stuti Pathak
C#
// C# implementation to check if vertex X
// lies in subgraph of vertex Y
// for the given graph
using System;
using System.Collections.Generic;
class GFG{
static int cnt = 1;
// Function ot perform dfs
static void dfs(List<int> []v, int []In,
int []Out, int []visited, int i)
{
// Mark visited of vertex i
visited[i] = 1;
// Update starting time
// of vertex i
In[i] = cnt;
// Increment the cnt
cnt++;
foreach(int x in v[i])
{
// Check if not visited
// call dfs from x
if (visited[x] == 0)
dfs(v, In, Out, visited, x);
}
// Update ending time
// of vertex i
Out[i] = cnt;
// Increment the cnt
cnt++;
}
// Function to add edges in graph
static void addedge(List<int> []v,
int x, int y)
{
v[x].Add(y);
v[y].Add(x);
}
// Function to check if vertex X
// lies in subgraph of vertex Y
// for the given graph
static bool is_subtree(List<int> []v,
int n, int m,
int x, int y)
{
// Arrays for starting time,
// ending time and to check
// for visited respectively
int []In = new int[n + 1];
int []Out = new int[n + 1];
int []visited = new int[n + 1];
// Mark all vertices starting time,
// ending time and visited as zero
for(int i = 1; i <= n; i++)
{
In[i] = 0;
Out[i] = 0;
visited[i] = 0;
}
// Check if y comes before x
// and leaves after x then x lies
// in the subgraph of y
// call dfs from any vertex,
// here we have called from 1
dfs(v, In, Out, visited, 1);
if (In[y] < In[x] && Out[y] > Out[x])
return true;
else
return false;
}
// Driver code
public static void Main(String[] args)
{
// n number of vertices
// m number of edges
int n = 6, m = 5;
// Create a graph given
// in the above diagram
List<int> []v = new List<int>[n + 1];
for(int i = 0; i < v.Length; i++)
v[i] = new List<int>();
addedge(v, 1, 2);
addedge(v, 1, 3);
addedge(v, 2, 4);
addedge(v, 1, 5);
addedge(v, 3, 6);
int x = 6, y = 1;
if (is_subtree(v, n, m, x, y))
Console.Write("Yes");
else
Console.Write("No");
}
}
// This code is contributed by Rohit_ranjan
Javascript
<script>
// javascript implementation to check if vertex X
// lies in subgraph of vertex Y
// for the given graph
var cnt = 1;
// Function ot perform dfs
function dfs(v, In, Out, visited, i)
{
// Mark visited of vertex i
visited[i] = 1;
// Update starting time
// of vertex i
In[i] = cnt;
// Increment the cnt
cnt++;
for(var x of v[i])
{
// Check if not visited
// call dfs from x
if (visited[x] == 0)
dfs(v, In, Out, visited, x);
}
// Update ending time
// of vertex i
Out[i] = cnt;
// Increment the cnt
cnt++;
}
// Function to add edges in graph
function addedge(v, x, y)
{
v[x].push(y);
v[y].push(x);
}
// Function to check if vertex X
// lies in subgraph of vertex Y
// for the given graph
function is_subtree(v, n, m, x, y)
{
// Arrays for starting time,
// ending time and to check
// for visited respectively
var In = Array(n+1).fill(0);
var Out = Array(n+1).fill(0);
var visited = Array(n+1).fill(0);
// Mark all vertices starting time,
// ending time and visited as zero
for(var i = 1; i <= n; i++)
{
In[i] = 0;
Out[i] = 0;
visited[i] = 0;
}
// Check if y comes before x
// and leaves after x then x lies
// in the subgraph of y
// call dfs from any vertex,
// here we have called from 1
dfs(v, In, Out, visited, 1);
if (In[y] < In[x] && Out[y] > Out[x])
return true;
else
return false;
}
// Driver code
// n number of vertices
// m number of edges
var n = 6, m = 5;
// Create a graph given
// in the above diagram
var v = Array.from(Array(n+1), ()=>Array());
addedge(v, 1, 2);
addedge(v, 1, 3);
addedge(v, 2, 4);
addedge(v, 1, 5);
addedge(v, 3, 6);
var x = 6, y = 1;
if (is_subtree(v, n, m, x, y))
document.write("Yes");
else
document.write("No");
</script>
Yes
Complejidad de tiempo: O(V + E)
Complejidad de espacio: O(3*N)
Publicación traducida automáticamente
Artículo escrito por harshsinghal93294 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA