Transformación rápida iterativa de Fourier para la multiplicación de polinomios

Dados dos polinomios, A(x) y B(x), encuentra el producto C(x) = A(x)*B(x). En la publicación anterior, discutimos el enfoque recursivo para resolver este problema que tiene una complejidad O (nlogn). 
Ejemplos: 
 

Input : 
 A[] = {9, -10, 7, 6}
 B[] = {-5, 4, 0, -2}
Output :
 C(x) =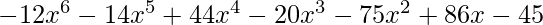 

En aplicaciones de la vida real, como el procesamiento de señales, la velocidad importa mucho, este artículo examina una implementación eficiente de FFT. Este artículo se centra en la versión iterativa del algoritmo FFT que se ejecuta en tiempo O (nlogn), pero puede tener una constante oculta más baja que la versión recursiva, además de que ahorra espacio en la pila de recursividad. 
Requisito previo : algoritmo recursivo de FFT. 
Recuerde el pseudocódigo recursivo-FFT de la publicación anterior, en la evaluación del ciclo for de  ,  se calcula dos veces. Podemos cambiar el ciclo para calcularlo solo una vez, almacenándolo en una variable temporal t. Entonces, se convierte en, 
para k  0 a n/2 – 1 
do t



La operación en este ciclo, multiplicando el factor twiddle w =  por , almacenar el producto en t y sumar y restar t de  , se conoce como operación mariposa. 
Gráficamente, así es como se ve una operación de mariposa: 
 

Consideremos n=8 y procedamos con la formación del algoritmo FFT iterativo. Mirando el árbol de recurrencia anterior, encontramos que si colocamos los elementos del vector de coeficiente inicial en el orden en que aparecen en las hojas, podríamos rastrear la ejecución del procedimiento Recursive-FFT, pero de abajo hacia arriba en lugar de arriba. -abajo. Primero, tomamos los elementos en pares, calculamos la DFT de cada par usando una operación de mariposa y reemplazamos el par con su DFT. Luego, el vector contiene n/2 DFT de 2 elementos. Luego, tomamos estos n/2 DFT en pares y calculamos el DFT de los cuatro elementos vectoriales de los que provienen ejecutando dos operaciones mariposa, reemplazando dos DFT de 2 elementos con un DFT de 4 elementos. Luego, el vector contiene n/4 DFT de 4 elementos. Continuamos de esta manera hasta que el vector tenga dos (n/2) elementos DFT, 
 

Para convertir este enfoque ascendente en código, usamos una array A[0…n] que inicialmente contiene los elementos del vector de entrada a en el orden en que aparecen en las hojas del árbol. Debido a que tenemos que combinar DFT en cada nivel del árbol, introducimos una variable s para contar los niveles, que van desde 1 (en la parte inferior, cuando estamos combinando pares para formar DFT de 2 elementos) hasta lgn (en la parte superior , cuando estamos combinando dos DFT de n/2 elementos para producir el resultado final). El algoritmo por lo tanto es: 
 

1. for s=1 to lgn
2.     do for k=0 to n-1 by 3.           do combine the two  -element DFTs in                A[k...k+-1] and A[k+...k+-1]                into one 2s-element DFT in A[k...k+-1]

Ahora, para generar el código, organizamos los elementos del vector de coeficientes en el orden de las hojas. Ejemplo: el orden en las hojas 0, 4, 2, 6, 1, 5, 3, 7 es una pequeña inversión de los índices. Comience con 000, 001, 010, 011, 100, 101, 110, 111 e invierta los bits de cada número binario para obtener 000, 100, 010, 110, 001, 101, 011, 111. Pseudocódigo para FFT iterativa: 
 

BIT-REVERSE-COPY(a, A)
n = length [a]
for k = 0 to n-1
        do A[rev(k)] = a[k]
 
ITERATIVE-FFT
BIT-REVERSE-COPY(a, A)
n = length(a)
for s = 1 to log n
        do m= 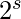 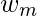   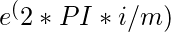   =              for j = 0 to m/2-1               do for k = j to n-1 by m                      do t = 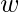A[k+m/2]                         u = A[k]                         A[k] = u+t                         A[k+m/2] = u-t  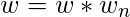return A

Será más claro a partir del siguiente circuito FFT paralelo: 
 

// CPP program to implement iterative
// fast Fourier transform.
#include <bits/stdc++.h>
using namespace std;
 
typedef complex<double> cd;
const double PI = 3.1415926536;
 
// Utility function for reversing the bits
// of given index x
unsigned int bitReverse(unsigned int x, int log2n)
{
    int n = 0;
    for (int i = 0; i < log2n; i++)
    {
        n <<= 1;
        n |= (x & 1);
        x >>= 1;
    }
    return n;
}
 
// Iterative FFT function to compute the DFT
// of given coefficient vector
void fft(vector<cd>& a, vector<cd>& A, int log2n)
{
    int n = 4;
 
    // bit reversal of the given array
    for (unsigned int i = 0; i < n; ++i) {
        int rev = bitReverse(i, log2n);
        A[i] = a[rev];
    }
 
    // j is iota
    const complex<double> J(0, 1);
    for (int s = 1; s <= log2n; ++s) {
        int m = 1 << s; // 2 power s
        int m2 = m >> 1; // m2 = m/2 -1
        cd w(1, 0);
 
        // principle root of nth complex
        // root of unity.
        cd wm = exp(J * (PI / m2));
        for (int j = 0; j < m2; ++j) {
            for (int k = j; k < n; k += m) {
 
                // t = twiddle factor
                cd t = w * A[k + m2];
                cd u = A[k];
 
                // similar calculating y[k]
                A[k] = u + t;
 
                // similar calculating y[k+n/2]
                A[k + m2] = u - t;
            }
            w *= wm;
        }
    }
}
 
int main()
{
    vector<cd> a{ 1, 2, 3, 4 };
    vector<cd> A(4);
    fft(a, A, 2);
    for (int i = 0; i < 4; ++i)
        cout << A[i] << "\n";
}

Input:  1 2 3 4
Output:
(10, 0)
(-2, -2)
(-2, 0)
(-2, 2)

Análisis de la complejidad del tiempo: 
La complejidad es O(nlgn). Para mostrar esto, mostramos que el ciclo más interno se ejecuta en tiempo O (nlgn) como: