Dada una array 2D , la tarea es convertirla en una lista doblemente enlazada con cuatro punteros que son siguiente, anterior, arriba y abajo, cada Node de esta lista debe estar conectado a sus Nodes siguiente, anterior, arriba y abajo. .
Ejemplos:
Input: 2D matrix 1 2 3 4 5 6 7 8 9 Output:
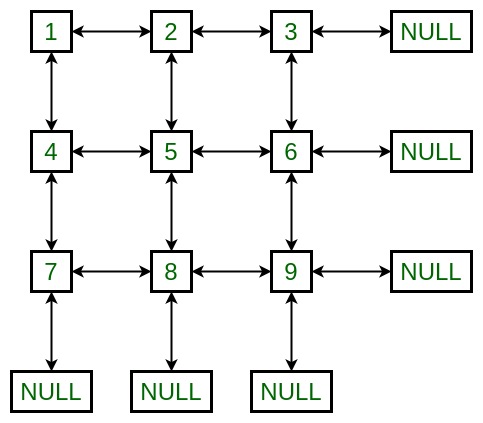
Enfoque: La idea principal es construir un nuevo Node para cada elemento de la array y crear recursivamente sus Nodes arriba, abajo, anterior y siguiente y cambiar el puntero de los punteros anterior y superior respectivamente.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program to construct a Doubly
// linked linked list from 2D Matrix
#include <iostream>
using namespace std;
// define dimension of matrix
#define dim 3
// struct node of doubly linked
// list with four pointer
// next, prev, up, down
struct Node {
int data;
Node* next;
Node* prev;
Node* up;
Node* down;
};
// function to create a new node
Node* createNode(int data)
{
Node* temp = new Node();
temp->data = data;
temp->next = NULL;
temp->prev = NULL;
temp->up = NULL;
temp->down = NULL;
return temp;
}
// function to construct the
// doubly linked list
Node* constructDoublyListUtil(
int mtrx[][dim],
int i, int j,
Node* curr)
{
if (i >= dim || j >= dim) {
return NULL;
}
// Create Node with value contain
// in matrix at index (i, j)
Node* temp = createNode(mtrx[i][j]);
// Assign address of curr into
// the prev pointer of temp
temp->prev = curr;
// Assign address of curr into
// the up pointer of temp
temp->up = curr;
// Recursive call for next pointer
temp->next
= constructDoublyListUtil(
mtrx, i, j + 1, temp);
// Recursive call for down pointer
temp->down
= constructDoublyListUtil(
mtrx, i + 1, j, temp);
// Return newly constructed node
// whose all four node connected
// at it's appropriate position
return temp;
}
// Function to construct the doubly linked list
Node* constructDoublyList(int mtrx[][dim])
{
// function call for construct
// the doubly linked list
return constructDoublyListUtil(
mtrx, 0, 0, NULL);
}
// function for displaying
// doubly linked list data
void display(Node* head)
{
// pointer to move right
Node* rPtr;
// pointer to move down
Node* dPtr = head;
// loop till node->down is not NULL
while (dPtr) {
rPtr = dPtr;
// loop till node->right is not NULL
while (rPtr) {
cout << rPtr->data << " ";
rPtr = rPtr->next;
}
cout << "\n";
dPtr = dPtr->down;
}
}
// driver code
int main()
{
// initialise matrix
int mtrx[dim][dim] = {
{ 1, 2, 3 },
{ 4, 5, 6 },
{ 7, 8, 9 }
};
Node* list = constructDoublyList(mtrx);
display(list);
return 0;
}
Java
// Java program to construct a Doubly
// linked linked list from 2D Matrix
import java.util.*;
class GFG{
// define dimension of matrix
static int dim= 3;
// struct node of doubly linked
// list with four pointer
// next, prev, up, down
static class Node {
int data;
Node next;
Node prev;
Node up;
Node down;
};
// function to create a new node
static Node createNode(int data)
{
Node temp = new Node();
temp.data = data;
temp.next = null;
temp.prev = null;
temp.up = null;
temp.down = null;
return temp;
}
// function to construct the
// doubly linked list
static Node constructDoublyListUtil(int mtrx[][],int i, int j,Node curr)
{
if (i >= dim || j >= dim) {
return null;
}
// Create Node with value contain
// in matrix at index (i, j)
Node temp = createNode(mtrx[i][j]);
// Assign address of curr into
// the prev pointer of temp
temp.prev = curr;
// Assign address of curr into
// the up pointer of temp
temp.up = curr;
// Recursive call for next pointer
temp.next
= constructDoublyListUtil(mtrx, i, j + 1, temp);
// Recursive call for down pointer
temp.down= constructDoublyListUtil(mtrx, i + 1, j, temp);
// Return newly constructed node
// whose all four node connected
// at it's appropriate position
return temp;
}
// Function to construct the doubly linked list
static Node constructDoublyList(int mtrx[][])
{
// function call for construct
// the doubly linked list
return constructDoublyListUtil(mtrx, 0, 0, null);
}
// function for displaying
// doubly linked list data
static void display(Node head)
{
// pointer to move right
Node rPtr;
// pointer to move down
Node dPtr = head;
// loop till node.down is not null
while (dPtr != null) {
rPtr = dPtr;
// loop till node.right is not null
while (rPtr!=null) {
System.out.print(rPtr.data+" ");
rPtr = rPtr.next;
}
System.out.print("\n");
dPtr = dPtr.down;
}
}
// driver code
public static void main(String args[])
{
// initialise matrix
int mtrx[][] = {
{ 1, 2, 3 },
{ 4, 5, 6 },
{ 7, 8, 9 }
};
Node list = constructDoublyList(mtrx);
display(list);
}
}
// This code is contributed by AbhiThakur
Python3
# Python3 program to construct # a Doubly linked linked list # from 2D Matrix # define dimension of matrix dim = 3 # struct node of doubly linked # list with four pointer # next, prev, up, down class Node: def __init__(self, data): self.data = data self.prev = None self.up = None self.down = None self.next = None # function to create a # new node def createNode(data): temp = Node(data); return temp; # function to construct the # doubly linked list def constructDoublyListUtil(mtrx, i, j, curr): if (i >= dim or j >= dim): return None; # Create Node with value # contain in matrix at # index (i, j) temp = createNode(mtrx[i][j]); # Assign address of curr into # the prev pointer of temp temp.prev = curr; # Assign address of curr into # the up pointer of temp temp.up = curr; # Recursive call for next # pointer temp.next= constructDoublyListUtil(mtrx, i, j + 1, temp); # Recursive call for down pointer temp.down= constructDoublyListUtil(mtrx, i + 1, j, temp); # Return newly constructed node # whose all four node connected # at it's appropriate position return temp; # Function to construct the # doubly linked list def constructDoublyList(mtrx): # function call for construct # the doubly linked list return constructDoublyListUtil(mtrx, 0, 0, None); # function for displaying # doubly linked list data def display(head): # pointer to move right rPtr = None # pointer to move down dPtr = head; # loop till node->down # is not NULL while (dPtr != None): rPtr = dPtr; # loop till node->right # is not NULL while (rPtr != None): print(rPtr.data, end = ' ') rPtr = rPtr.next; print() dPtr = dPtr.down; # Driver code if __name__=="__main__": # initialise matrix mtrx =[[1, 2, 3], [4, 5, 6], [7, 8, 9]] list = constructDoublyList(mtrx); display(list); # This code is contributed by Rutvik_56
C#
// C# program to construct a Doubly
// linked linked list from 2D Matrix
using System;
class GFG{
// define dimension of matrix
static int dim= 3;
// struct node of doubly linked
// list with four pointer
// next, prev, up, down
public class Node {
public int data;
public Node next, prev, up, down;
};
// function to create a new node
static Node createNode(int data)
{
Node temp = new Node();
temp.data = data;
temp.next = null;
temp.prev = null;
temp.up = null;
temp.down = null;
return temp;
}
// function to construct the
// doubly linked list
static Node constructDoublyListUtil(int[,] mtrx,int i, int j,Node curr)
{
if (i >= dim || j >= dim) {
return null;
}
// Create Node with value contain
// in matrix at index (i, j)
Node temp = createNode(mtrx[i,j]);
// Assign address of curr into
// the prev pointer of temp
temp.prev = curr;
// Assign address of curr into
// the up pointer of temp
temp.up = curr;
// Recursive call for next pointer
temp.next
= constructDoublyListUtil(mtrx, i, j + 1, temp);
// Recursive call for down pointer
temp.down= constructDoublyListUtil(mtrx, i + 1, j, temp);
// Return newly constructed node
// whose all four node connected
// at it's appropriate position
return temp;
}
// Function to construct the doubly linked list
static Node constructDoublyList(int[,] mtrx)
{
// function call for construct
// the doubly linked list
return constructDoublyListUtil(mtrx, 0, 0, null);
}
// function for displaying
// doubly linked list data
static void display(Node head)
{
// pointer to move right
Node rPtr;
// pointer to move down
Node dPtr = head;
// loop till node.down is not null
while (dPtr != null) {
rPtr = dPtr;
// loop till node.right is not null
while (rPtr!=null) {
Console.Write(rPtr.data+" ");
rPtr = rPtr.next;
}
Console.Write("\n");
dPtr = dPtr.down;
}
}
// driver code
public static void Main()
{
// initialise matrix
int[,] mtrx = {
{ 1, 2, 3 },
{ 4, 5, 6 },
{ 7, 8, 9 }
};
Node list = constructDoublyList(mtrx);
display(list);
}
}
// This code is contributed by AbhiThakur
Javascript
<script>
// javascript program to construct a Doubly
// linked linked list from 2D Matrix
// define dimension of matrix
var dim = 3;
// struct node of doubly linked
// list with four pointer
// next, prev, up, down
class Node
{
constructor()
{
this.data = 0;
this.next = null;
this.prev = null;
this.up = null;
this.down = null;
}
}
// function to create a new node
function createNode(data)
{
temp = new Node();
temp.data = data;
temp.next = null;
temp.prev = null;
temp.up = null;
temp.down = null;
return temp;
}
// function to construct the
// doubly linked list
function constructDoublyListUtil(mtrx, i , j, curr)
{
if (i >= dim || j >= dim) {
return null;
}
// Create Node with value contain
// in matrix at index (i, j)
var temp = createNode(mtrx[i][j]);
// Assign address of curr into
// the prev pointer of temp
temp.prev = curr;
// Assign address of curr into
// the up pointer of temp
temp.up = curr;
// Recursive call for next pointer
temp.next
= constructDoublyListUtil(mtrx, i, j + 1, temp);
// Recursive call for down pointer
temp.down= constructDoublyListUtil(mtrx, i + 1, j, temp);
// Return newly constructed node
// whose all four node connected
// at it's appropriate position
return temp;
}
// Function to construct the doubly linked list
function constructDoublyList(mtrx)
{
// function call for construct
// the doubly linked list
return constructDoublyListUtil(mtrx, 0, 0, null);
}
// function for displaying
// doubly linked list data
function display( head)
{
// pointer to move right
rPtr = null;
// pointer to move down
dPtr = head;
// loop till node.down is not null
while (dPtr != null) {
rPtr = dPtr;
// loop till node.right is not null
while (rPtr != null)
{
document.write(rPtr.data + " ");
rPtr = rPtr.next;
}
document.write("<br/>");
dPtr = dPtr.down;
}
}
// driver code
// initialise matrix
var mtrx = [
[ 1, 2, 3 ],
[ 4, 5, 6 ],
[ 7, 8, 9 ]
];
var list = constructDoublyList(mtrx);
display(list);
// This code is contributed by todaysgaurav
</script>
1 2 3 4 5 6 7 8 9
Método 2: enfoque iterativo
Haremos uso de Nodes ficticios para marcar el inicio de los punteros up y prev. También en el enfoque anterior, estamos creando tantos Nodes adicionales que aquí no crearemos muchos Nodes adicionales.
Este enfoque funciona mejor en el caso de una array 2D grande, ya que no recibe llamadas recursivas generales.
C++
#include<bits/stdc++.h>
using namespace std;
struct Node {
int data; // To hold the value of matrix
// 4 pointers for left, right, up, down for markings.
Node* left;
Node* right;
Node* up;
Node* down;
Node(int x) : data(x) , left(NULL) , right(NULL) , up(NULL) , down(NULL) {}
};
void print(Node* head) {
// Require 2 pointers, downptr and rightptr, for rows and columns.
Node* downptr = head;
Node* rightptr;
while (downptr) {
rightptr = downptr;
while (rightptr) {
cout << (rightptr->data) << " ";
rightptr = rightptr->right;
}
cout << "\n";
downptr = downptr->down;
}
}
//Driver Code
int main() {
int mat[3][3] = {
{ 1, 2, 3 },
{ 4, 5, 6 },
{ 7, 8, 9 }
};
int n = 3, m = 3;
Node* head_main = NULL; // head of our final modified doubly linked list from 2d matrix.
Node* prev, *upper = new Node(-1); // dummy node to mark start of up pointer.
for (int i = 0; i < n; i++) {
Node* head_row; //row-wise head of list.
Node *prev = new Node(-1); // dummy node to mark start of left pointer.
for (int j = 0; j < m; j++) {
Node* temp = new Node(mat[i][j]);
if (j == 0) head_row = temp;
if (i == 0 && j == 0) head_main = temp;
temp->left = prev;
prev->right = temp;
if (i == n - 1) temp->down = NULL;
//This is only used for 1st row.
if (!upper->right) {
upper->right = new Node(-1);
}
upper = upper->right;
temp->up = upper;
upper->down = temp;
prev = temp;
if (j == m - 1) prev->right = NULL;
}
upper = head_row->left;
}
print(head_main);
return 0;
}
Java
import java.util.*;
public class Main {
static class Node {
int data; // To hold the value of matrix
// 4 pointers for left, right, up, down for
// markings.
Node left;
Node right;
Node up;
Node down;
Node(int x)
{
data = x;
left = null;
right = null;
up = null;
down = null;
}
}
public static void print(Node head)
{
// Require 2 pointers, downptr and rightptr, for
// rows and columns.
Node downptr = head;
Node rightptr;
while (downptr != null) {
rightptr = downptr;
while (rightptr != null) {
System.out.print(rightptr.data + " ");
rightptr = rightptr.right;
}
System.out.println();
downptr = downptr.down;
}
}
public static void main(String[] args)
{
int[][] mat
= { { 1, 2, 3 }, { 4, 5, 6 }, { 7, 8, 9 } };
int n = 3, m = 3;
Node head_main
= null; // head of our final modified doubly
// linked list from 2d matrix.
Node prev, upper
= new Node(-1); // dummy node to mark
// start of up pointer.
for (int i = 0; i < n; i++) {
Node head_row
= new Node(-1); // row-wise head of list.
prev = new Node(-1); // dummy node to mark start
// of left pointer.
for (int j = 0; j < m; j++) {
Node temp = new Node(mat[i][j]);
if (j == 0)
head_row = temp;
if (i == 0 && j == 0)
head_main = temp;
temp.left = prev;
prev.right = temp;
if (i == n - 1)
temp.down = null;
// This is only used for 1st row.
if (upper.right == null)
upper.right = new Node(-1);
upper = upper.right;
temp.up = upper;
upper.down = temp;
prev = temp;
if (j == m - 1)
prev.right = null;
}
upper = head_row.left;
}
print(head_main);
}
}
// This code is contributed by Tapesh(tapeshdua420)
Python3
# Python implementation of construction # of a Doubly linked linked list from 2D Matrix class Node: def __init__(self, data): self.data = data # To hold the value of matrix # 4 pointers for left, right, up, down for markings. self.left = None self.right = None self.up = None self.down = None def printList(head): # 4 pointers for left, right, up, down for markings. downptr = head rightptr = None while downptr != None: rightptr = downptr while rightptr != None: print(rightptr.data, end=" ") rightptr = rightptr.right print() downptr = downptr.down if __name__ == "__main__": mat = [ [1, 2, 3], [4, 5, 6], [7, 8, 9] ] n = 3 m = 3 # head of our final modified doubly linked list from 2d matrix. head_main = None prev = None upper = Node(-1) # dummy node to mark start of up pointer. for i in range(n): head_row = None # row-wise head of list. prev = Node(-1) # dummy node to mark start of left pointer. for j in range(m): temp = Node(mat[i][j]) if j == 0: head_row = temp if i == 0 and j == 0: head_main = temp temp.left = prev prev.right = temp if i == n-1: temp.down = None # This is only used for 1st row. if upper.right == None: upper.right = Node(-1) upper = upper.right temp.up = upper upper.down = temp prev = temp if j == m-1: prev.right = None upper = head_row.left printList(head_main) # This code is contributed by Tapesh (tapeshdua420)
C#
// C# implementation of construction
// of a Doubly linked linked list from 2D Matrix
using System;
class Program {
// Driver Code
static void Main(string[] args)
{
int[, ] mat
= { { 1, 2, 3 }, { 4, 5, 6 }, { 7, 8, 9 } };
int n = 3, m = 3;
Node head_main
= null; // head of our final modified doubly
// linked list from 2d matrix.
Node prev, upper
= new Node(-1); // dummy node to mark
// start of up pointer.
for (int i = 0; i < n; i++) {
Node head_row
= new Node(-1); // row-wise head of list.
prev = new Node(-1); // dummy node to mark start
// of left pointer.
for (int j = 0; j < m; j++) {
Node temp = new Node(mat[i, j]);
if (j == 0)
head_row = temp;
if (i == 0 && j == 0)
head_main = temp;
temp.left = prev;
prev.right = temp;
if (i == n - 1)
temp.down = null;
// This is only used for 1st row.
if (upper.right == null)
upper.right = new Node(-1);
upper = upper.right;
temp.up = upper;
upper.down = temp;
prev = temp;
if (j == m - 1)
prev.right = null;
}
upper = head_row.left;
}
print(head_main);
}
public static void print(Node head)
{
// Require 2 pointers, downptr and rightptr, for
// rows and columns.
Node downptr = head;
Node rightptr;
while (downptr != null) {
rightptr = downptr;
while (rightptr != null) {
Console.Write(rightptr.data + " ");
rightptr = rightptr.right;
}
Console.WriteLine();
downptr = downptr.down;
}
}
}
class Node {
public int data; // To hold the value of matrix
// 4 pointers for left, right, up, down for markings.
public Node left;
public Node right;
public Node up;
public Node down;
public Node(int x)
{
data = x;
left = null;
right = null;
up = null;
down = null;
}
}
// This code is contributed by Tapesh(tapeshdua420)
Javascript
<script>
// JavaScript implementation of construction
// of a Doubly linked linked list from 2D Matrix
class Node {
// To hold the value of matrix
// 4 pointers for left, right, up, down for markings.
constructor(x)
{
this.data = x;
this.left = null;
this.right = null;
this.up = null;
this.down = null;
}
}
function print(head)
{
// Require 2 pointers, downptr and rightptr, for rows and columns.
let downptr = head;
let rightptr;
while (downptr) {
rightptr = downptr;
while (rightptr) {
document.write(rightptr.data," ");
rightptr = rightptr.right;
}
document.write("</br>");
downptr = downptr.down;
}
}
// Driver Code
let mat = [
[ 1, 2, 3 ],
[ 4, 5, 6 ],
[ 7, 8, 9 ]
];
let n = 3, m = 3;
let head_main = null; // head of our final modified doubly linked list from 2d matrix.
let prev, upper = new Node(-1); // dummy node to mark start of up pointer.
for (let i = 0; i < n; i++) {
let head_row; //row-wise head of list.
let prev = new Node(-1); // dummy node to mark start of left pointer.
for (let j = 0; j < m; j++) {
let temp = new Node(mat[i][j]);
if (j == 0) head_row = temp;
if (i == 0 && j == 0) head_main = temp;
temp.left = prev;
prev.right = temp;
if (i == n - 1) temp.down = null;
//This is only used for 1st row.
if (!upper.right) {
upper.right = new Node(-1);
}
upper = upper.right;
temp.up = upper;
upper.down = temp;
prev = temp;
if (j == m - 1) prev.right = null;
}
upper = head_row.left;
}
print(head_main)
// This code is contributed by shinjanpatra
</script>
Producción:
1 2 3 4 5 6 7 8 9
Complejidad de tiempo : O(n*m) donde n representa el número de filas, m representa el número de columnas en nuestra array.
Complejidad espacial: O(1) espacio extra constante.
Publicación traducida automáticamente
Artículo escrito por MohammadMudassir y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA